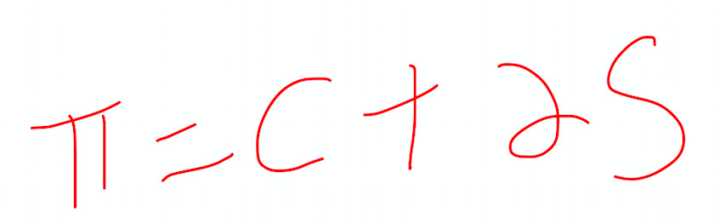在上述几篇文章的铺垫之后,我们终于开始推导我们的Black-Scholes方程
当我们考虑越多的东西之后,就会变得越复杂,就跟我们上一篇文章的推导的东西,在之前是不能推导的,之后在Black-Scholes把这个东西推导出来之后,然后获得诺贝尔奖.
下面我们来欣赏诺贝尔奖的作品:
在下边的过程中,我们先要推导他的动力学方程,推到完动力学方程之后再去应用动力学方程推出他的结论.就相当于我们要推倒氢原子的基态能级,但是我们现在连薛定谔方程都没有,我们先把薛定谔方程推出来.
我们首先看一个Black-Scholes方程的基本假设,他是假设股票是如何做刚才所说的这样的一个随机游走,在这里,我们先定义一下所需要的参数:
S:Stock Price(股票价格)
C:Call option(看涨期权的价格)
f(S,t)=C(S,t),C会是一个关于S和t的函数
那接下来我们要去研究这个随机游走,随机游走我们这样看,股票的价格应该有两种变量,一种变量就是股票价格像是钱一样,股票的价格像是一个公开上市公司的一部分,所以这样的股份叫做share,那随着社会的演化,这个公司会不断的持续去创造财富,然后这个公司的股价或者这个公司在社会上的重要性一直在增加,而这个公司的股价也会有一个指数增长,这个是可以理解的,的确我们看到的股市也的确是这样的,就是如果我们把比如SNP500指数(标普500指数)我们画出来的话,他会是一个平均值不断上升的函数,这是一个观察结论,所以我们认为股票他的随机游走,除了一个随机的部分还会有一个人为的一个指数增长的部分,而这个部分我们很熟悉:
那另外一个随机部分,我们是这样认为的,首先他会有dw,并且我们会乘以一个系数,但是我们会认为dw是股价相对于自己已经有的一个股价的涨落,也就是说他随机游走是指数型的随机的游走,他随机的涨1%而不是随机的涨1美元,就是说他的股价越高的时候,他的涨落部分越大,所以他应该乘以S,所以我们认为这个是OK的,
所以我们把它整合成
大家还知道dw的方差是多少么?是△t,但是并不是所有的股票他的游走的方差都是一样的,一个股票应该有自己的一些特性,而这个股票的波动性我们认为前后应该是相同的,所以前边的不同的股票会有一个Σ,然后因为方差是dt,所以新的方差就会变成∑dt²,所以说我们认为dw前边的系数就是标准差,所以这样的一个∑的意义很明确的 ,那这个系数就叫做波动率
那接下来就是一个纯数学的构造,在数学上我们想做一个纯投资组合,我们想说我们制造一种东西叫做π,π是一部分的看涨期权加上一部分的股票混合起来,人为构造的.
至于说那个基金经理回去买这样的一个投资组合,这个无所谓,因为接下我会有神奇的效果,然后我们希望的是能不能存在这样的一个投资组合他是有看涨期权加上股票配合起来,使得这样的一个投资组合是跟dw无关的或者是没有涨落的部分,我们试着去构造一下:因为我们知道,这个看涨期权是跟dw有关,因为他在游走,股票也跟dw有关,因为他也在游走,如果他们两个可以很好地消去的话,那么他就会变成一个无游走的资产,而无游走的资产就跟现金一样,我们会知道他会怎么发展,就跟放银行了,而这时推导公式的最核心的思想,就是无中生有出的一个投资组合.
这其中要知道的就是α,就是他们之间的如何配比,因为配比一旦确定,一旦乘以10也是可以确定的,那我们现在朝着无风险的投资组合前进,如果已经构造出无风险的话我们就应该把他表示出:
并且后边的系数是0那是我们的目标,所以我们现在就把dπ直接展开,让系数等于0看看会有什么发生:
而上边的只是一个大概,而下一篇文章我们将使用B-S方程来去求看涨期权的精确解!