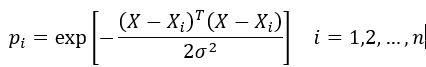本文同步于微信公众号【知行阿明】
欢迎关注微信公众号,获取更多优秀文章!
案例背景
广义回归神经网络(GRNN,Generalized Regression Neural Network)是美国学者Donald F.Specht在1991年提出的,它是径向基神经网络的一种。GRNN具有很强的非线性映射能力和柔性网络结构以及高度的容错性和鲁棒性,适用于解决非线性问题。
GRNN在逼近能力和学习速度上较RBF网络有更强的优势,网络最后收敛域样本量积聚较多的优化回归面,并且在样本数据较少时,预测效果也较好。
此外,GRNN网络还可以处理不稳定的数据,因此,GRNN在信号处理、结构分析、教育产业、能源、食品科学、控制决策系统、药物设计、金融领域、生物工程等各个领域得到了广泛的应用。
GRNN在结构上与RBF网络较为相似。它由四层构成,如下图1所示,分别为输入层(input layer)、模式层(pattern layer)、求和层(simulation layer)和输出层(output layer)。
对应网络输入为X=[x1,x2,...,xn],输出为Y=[y1,y2,...,yk]。
输入层
输入层神经元的数目等于学习样本中输入向量的维数,各神经元是简单的分布单元,直接将输入变量传递给模式层-
模式层
模式层神经元数目等于学习样本的数目n,各神经元对应不同的样本,模式层神经元传递函数为
神经元i的输出为输入变量与其对应的样本X之间欧式距离平方的指数平方。
-
求和层
求和层使用两种类型神经元进行求和。
一类的计算公式为
它对所有模式层神经元的输出进行算术求和,其模式层与各神经元的连接权值为1,传递函数为
另一类计算公式为
它对所有模式层的神经元进行加权求和,模式层中第i个神经元与求和层中第j个分子求和神经元之间的连接权值为第i个输出样本Yi中的第j个元素,传递函数为
-
输出层
输出层中的神经元数目等于学习样本中输出向量的维数k,各神经元将求和层的输出相除,神经元j的输出对应估计结果Y(X)的第j个元素,即
建立模型
根据货运量影响因素的分析,分别取国内生产总值(GDP)、工业总产值、铁路运输线路长度、复线里程比重、公路运输线路长度、等级公路比重、铁路货车数量和民用货车数量8项指标因素作为网络输入,以货运总量、铁路货运量和公路货运量3项指标因素作为网络输出,构建GRNN,由于训练数据较少,采取交叉验证方法训练GRNN神经网络,并用循环找出最佳的SPREAD。
本文中data.mat中共有p、t两组数据,又各含13组数据,代表了1996-2008年的货运量和与其相关的各个变量值。将p、t的前12组数据作为网络的训练数据,最后1组数据作为网络的预测数据,建立GRNN神经网络对货运量进行预测。
MATLAB实现
% GRNN的数据预测—基于广义回归神经网络的货运量预测
%% 清空环境变量
clc;
clear all
close all
nntwarn off;
%% 载入数据
load data;
% 载入数据并将数据分成训练和预测两类
p_train=p(1:12,:);
t_train=t(1:12,:);
p_test=p(13,:);
t_test=t(13,:);
%% 交叉验证
desired_spread=[];
mse_max=10e20;
desired_input=[];
desired_output=[];
result_perfp=[];
indices = crossvalind('Kfold',length(p_train),4);
h=waitbar(0,'正在寻找最优化参数....');
k=1;
for i = 1:4
perfp=[];
disp(['以下为第',num2str(i),'次交叉验证结果'])
test = (indices == i); train = ~test;
p_cv_train=p_train(train,:);
t_cv_train=t_train(train,:);
p_cv_test=p_train(test,:);
t_cv_test=t_train(test,:);
p_cv_train=p_cv_train';
t_cv_train=t_cv_train';
p_cv_test= p_cv_test';
t_cv_test= t_cv_test';
[p_cv_train,minp,maxp,t_cv_train,mint,maxt]=premnmx(p_cv_train,t_cv_train);
p_cv_test=tramnmx(p_cv_test,minp,maxp);
for spread=0.1:0.1:2;
net=newgrnn(p_cv_train,t_cv_train,spread);
waitbar(k/80,h);
disp(['当前spread值为', num2str(spread)]);
test_Out=sim(net,p_cv_test);
test_Out=postmnmx(test_Out,mint,maxt);
error=t_cv_test-test_Out;
disp(['当前网络的mse为',num2str(mse(error))])
perfp=[perfp mse(error)];
if mse(error)输出为
最佳spread值为0.9
此时最佳输入值为
desired_input =
1 至 8 列
-1.0000 -0.9578 -0.8593 -0.7570 -0.4706 -0.2682 0.1779 0.3968
-0.9550 -0.9998 -1.0000 -0.1291 -0.0072 0.2070 0.5137 0.6187
-1.0000 -1.0000 -0.8616 -0.4969 -0.4969 0.1950 0.4465 0.6478
-1.0000 -1.0000 -0.5385 -0.0769 0.5385 0.2308 0.3846 0.6923
-1.0000 -0.9749 -0.9185 -0.8934 -0.7555 -0.5737 -0.0157 0.2602
-1.0000 -0.7391 -0.7391 -0.7391 -0.3043 -0.1304 0.1304 0.3043
0.0114 0.0141 -1.0000 0.0187 0.0187 0.2477 0.4944 0.6195
-1.0000 -0.7677 -0.6979 -0.6639 -0.7291 -0.5720 -0.1527 0.0881
9 列
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
此时最佳输出值为
desired_output =
1 至 8 列
-1.0000 -0.9931 -0.9771 -0.9770 -0.7068 -0.4453 0.0160 0.2887
-1.0000 -0.9401 -0.8469 -0.8046 -0.5911 -0.3532 -0.0446 0.2360
-1.0000 -0.9512 -0.7580 -0.7602 -0.5070 -0.2167 0.0650 0.2688
9 列
1.0000
1.0000
1.0000
GRNN神经网络三项流量预测的误差为12648.9501 3514.0533 15920.1375
由程序运行后的结果中看出,SPREAD值设置为0.9时,训练数据的预测较好。
SPREAD值越小,网络对样本的逼近性就越强;SPREAD值越大,网络对样本数据的逼近过程就越平滑,但误差也相应增大。
在实际应用时,为了选取最佳的SPREAD值,一般采取本文中的循环训练方法,从而达到最好的预测效果。
长按二维码关注,与阿明一起成长!
每一次的旅行
都想与你同在