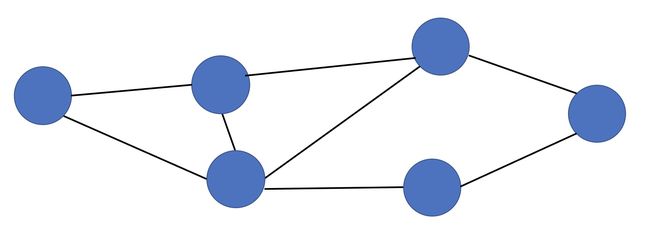
图是由顶点和顶点之间边组成的一种数据结构。如下图所示:
加权图
在加权图中,每一条边都有一个权重,我们可以利用这个权重来计算除图中两个顶点的最小路径。
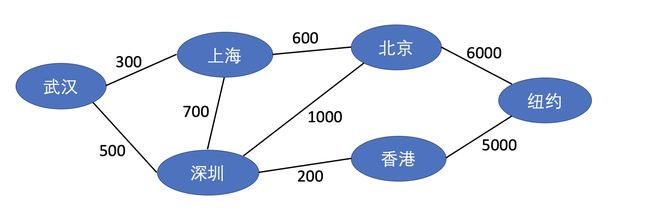
假设有以下虚构的航班路线路:
图中顶点代表一个地点,边代表从一个地点到另外一个地点的路线,而权重代表机票的费用。根据这个图,我们可以计算出从武汉到纽约机票最少的路线。
有向图
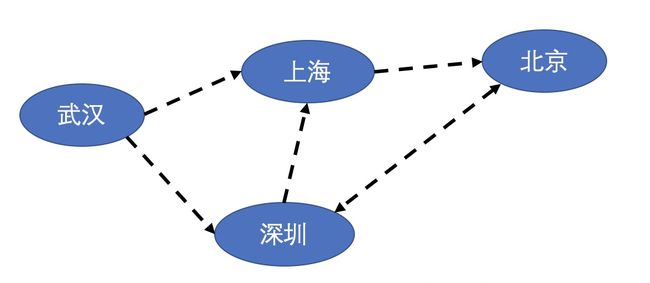
图的边除了可以有权重之外,还可以有方向,而且可以是双向或者是单向的。如下图:
无向图
我们可以把无向图看作是一个所有边都是双向的有向图。如下图:
代码实现
因为图有顶点和边组成,我们首先定义好顶点和边。
顶点和边
struct Vertex {
let index: Int
let value: T
}
extension Vertex: Hashable {
var hashValue: Int {
return index.hashValue
}
static func == (lhs: Vertex, rhs: Vertex) -> Bool {
return lhs.index == rhs.index
}
}
extension Vertex: CustomStringConvertible {
var description: String {
return "\(index): \(value)"
}
}
Vertex 定义为泛型,index 为顶点被添加到图中的先后顺序,value 为顶点所包含的值。因为在后面的实现中,顶点要作为字典中的 key,所以实现了 Hashable 协议。最后实现了 CustomStringConvertible。
struct Edge {
let source: Vertex
let destination: Vertex
let weight: Double?
}
source 表示边的起点,destination 表示边的终点,weight 是边的权重。
Graph 协议
图的实现方式有两种:邻接表和邻接矩阵。在用邻接表和邻接矩阵实现图之前,我们先创建一个 Graph 协议,然后在实现的时候遵循这个协议。
enum EdgeType {
case directed
case undirected
}
protocol Graph {
associatedtype Element
// 创建顶点
func createVertex(value: Element) -> Vertex
// 在两个顶点中添加有向的边
func addDirectedEdge(from source: Vertex,
to destination: Vertex,
weight: Double?)
// 在两个顶点中添加无向的边
func addUndirectedEdge(between source: Vertex,
and destination: Vertex,
weight: Double?)
// 根据边的类型在两个顶点中添加边
func addEdge(_ edge: EdgeType,
from source: Vertex,
to destination: Vertex,
weight: Double?)
// 返回从某个顶点发出去的所有边
func edges(from source: Vertex) -> [Edge]
// 返回从一个顶点到另个顶点的边的权重
func weight(from source: Vertex,
to destination: Vertex) -> Double?
}
因为边分有向和无向,所以先定义一个 EdgeType。Graph 的代码解释请看注释。
邻接表
首先我们看如何用邻接表来实现图。
final class AdjacencyList {
private var adjacencies: [Vertex: [Edge]] = [:]
init() { }
}
extension AdjacencyList: Graph {
func createVertex(value: T) -> Vertex {
let vertex = Vertex(index: adjacencies.count, value: value)
adjacencies[vertex] = []
return vertex
}
func addDirectedEdge(from source: Vertex, to destination: Vertex, weight: Double?) {
let edge = Edge(source: source, destination: destination, weight: weight)
adjacencies[source]?.append(edge)
}
func edges(from source: Vertex) -> [Edge] {
return adjacencies[source] ?? []
}
func weight(from source: Vertex, to destination: Vertex) -> Double? {
return edges(from: source)
.first { $0.destination == destination }?
.weight
}
}
extension AdjacencyList: CustomStringConvertible {
var description: String {
var result = ""
for (vertex, edges) in adjacencies {
var edgeString = ""
for (index, edge) in edges.enumerated() {
if index < edges.count - 1 {
edgeString.append("\(edge.destination), ")
} else {
edgeString.append("\(edge.destination)")
}
}
result.append("\(vertex) --> [ \(edgeString) ]\n")
}
return result
}
}
我们用一个字典 adjacencies 来存储从某个顶点发出的边。
然后是实现 Graph 协议,这里只实现了四个方法,剩下的两个方法,可以直接在 Graph 提供默认的实现:
extension Graph {
// 在两个顶点中添加无向的边,也就相当于在两个顶点之间互相添加有向图
func addUndirectedEdge(between source: Vertex,
and destination: Vertex,
weight: Double?) {
addDirectedEdge(from: source, to: destination, weight: weight)
addDirectedEdge(from: destination, to: source, weight: weight)
}
// 根据边的类型在两个顶点中添加边,可以直接根据边的类型调用协议里的其他方法来实现
func addEdge(_ edge: EdgeType,
from source: Vertex,
to destination: Vertex,
weight: Double?) {
switch edge {
case .directed:
addDirectedEdge(from: source, to: destination, weight: weight)
case .undirected:
addUndirectedEdge(between: source, and: destination, weight: weight)
}
}
}
最后是实现了 CustomStringConvertible 协议,在打印的时候以这种格式显示出来:顶点 --> [ 从顶点出发的所有终点 ],例如 4: 香港 --> [ 2: 深圳, 5: 纽约 ]。
以文章开头的加权图为例,测试一下我们写的代码:
let graph = AdjacencyList()
let wuHan = graph.createVertex(value: "武汉")
let shangHai = graph.createVertex(value: "上海")
let shenZhen = graph.createVertex(value: "深圳")
let beiJing = graph.createVertex(value: "北京")
let hongKong = graph.createVertex(value: "香港")
let newYork = graph.createVertex(value: "纽约")
graph.addEdge(.undirected, from: wuHan, to: shangHai, weight: 300)
graph.addEdge(.undirected, from: wuHan, to: shenZhen, weight: 500)
graph.addEdge(.undirected, from: shangHai, to: shenZhen, weight: 700)
graph.addEdge(.undirected, from: shangHai, to: beiJing, weight: 600)
graph.addEdge(.undirected, from: shenZhen, to: beiJing, weight: 1000)
graph.addEdge(.undirected, from: shenZhen, to: hongKong, weight: 200)
graph.addEdge(.undirected, from: beiJing, to: newYork, weight: 6000)
graph.addEdge(.undirected, from: hongKong, to: newYork, weight: 5000)
print(graph)
// 结果
4: 香港 --> [ 2: 深圳, 5: 纽约 ]
5: 纽约 --> [ 3: 北京, 4: 香港 ]
2: 深圳 --> [ 0: 武汉, 1: 上海, 3: 北京, 4: 香港 ]
0: 武汉 --> [ 1: 上海, 2: 深圳 ]
1: 上海 --> [ 0: 武汉, 2: 深圳, 3: 北京 ]
3: 北京 --> [ 1: 上海, 2: 深圳, 5: 纽约 ]
邻接矩阵
邻接矩阵用一个正方形的矩阵来表示一个图。矩阵由一个二维数组组成。matrix[1][2] 对应的值是在索引为 1 的顶点到索引为 2 的顶点的边的权重。
以下面这个有向航空票价图为例:
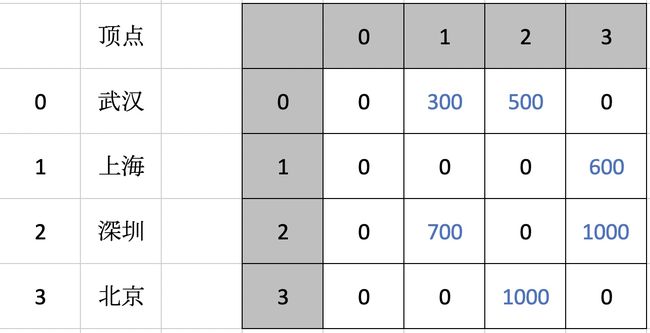
我们可以得到一个矩阵图如下:
左边顶点前面的数字代表顶点被加入图时的位置,右边行号表示出发点,列号表示终点。例如:
-
[0][1]代表武汉到深圳的票价为 300; -
[2][1]代表深圳到上海的票价为 700。
代码实现
final class AdjacencyMatrix {
private var vertices: [Vertex] = []
private var weights: [[Double?]] = []
init() { }
}
extension AdjacencyMatrix: Graph {
func createVertex(value: T) -> Vertex {
let vertex = Vertex(index: vertices.count, value: value)
vertices.append(vertex)
for i in 0.., to destination: Vertex, weight: Double?) {
weights[source.index][destination.index] = weight
}
func edges(from source: Vertex) -> [Edge] {
var edges: [Edge] = []
for column in 0.., to destination: Vertex) -> Double? {
return weights[source.index][destination.index]
}
}
extension AdjacencyMatrix: CustomStringConvertible {
var description: String {
let verticesDes = vertices.map { "\($0)" }
.joined(separator: "\n")
var grid: [String] = []
for i in 0..vertices 存储所有的顶点,weights 存储所有边的权重。
Graph的协议只需实现四个方法即可,另外两个方法在邻接表那一部分已经提供默认的实现。
最后是实现了 CustomStringConvertible 协议,在打印的时候把所有边的权重显示出来,如果没有值,则显示 ø。
以这一节的有向航空票价图为例,创建的图如下:
let graph = AdjacencyMatrix()
let wuHan = graph.createVertex(value: "武汉")
let shangHai = graph.createVertex(value: "上海")
let shenZhen = graph.createVertex(value: "深圳")
let beiJing = graph.createVertex(value: "北京")
graph.addDirectedEdge(from: wuHan, to: shangHai, weight: 300)
graph.addDirectedEdge(from: wuHan, to: shenZhen, weight: 500)
graph.addDirectedEdge(from: shangHai, to: beiJing, weight: 600)
graph.addDirectedEdge(from: shenZhen, to: shangHai, weight: 700)
graph.addUndirectedEdge(between: shenZhen, and: beiJing, weight: 1000)
print(graph)
结果如下图:
性能分析
邻接表和邻接矩阵实现图的性能对比如下, V 代表顶点,E 代表边:
| 操作 | 邻接表 | 邻接矩阵 |
|---|---|---|
| 存储空间 | O(V + E) | O(V^2) |
| 添加顶点 | O(1) | O(V^2) |
| 添加边 | O(1) | O(1) |
| 查找边和权重 | O(V) | O(1) |
邻接表所需的存储空间小于邻接矩阵,邻接表可以直接存储顶点和边,而邻接矩阵需要用个二维数组来存储边,二维数组元素个数就等于顶点的个数,所以是O(V^2)。
邻接表添加顶点,直接存入字典即可,所以是 O(1)。邻接矩阵添加顶点,需要在二维数组添加多一行和一列,时间复杂度至少是 O(V),如果矩阵由一个连续的内存区域存储,有可能是 O(V^2)。
邻接表添加边,直接在字典中key对应的数组添加元素;邻接矩阵添加边,直接更改二维数组的其中一个元素,都是 O(1)。
邻接表查找某条边和权重,需要找到从某个顶点出发的所有边,然后通过循环找到特定的边,所以最坏的情况下是 O(V)。邻接矩阵查找某条边和权重,能直接从二维数组中找到对应的元素,所以时间是 O(1)。
邻接表和邻接矩阵,我们如何选择?如果我们的图中边的数量不多,选择邻接表,因为邻接矩阵所需的内存比较大。如果我们的图有很多边,选择邻接矩阵比较好,因为他在查找边和权重上速度较快。
完整代码 >>
参考资料
Data Structures and Algorithms in Swift --- raywenderlich.com,如果想看原版书籍,请点击链接购买。
完
欢迎加入我管理的Swift开发群:536353151。