1. 常见分布
这里讨论几个常见的概率分布,而它们之间存在着紧密的关联。很多复杂的概率模型其实有着更简单的底层原理,这种联系再次验证了随机现象的确定性方面。看似复杂随机现象其实就是由许多“原子事件”组合而成,数学的规律仍然起着支配作用。
1.1 伯努利试验
最简单且有意义的事件域是\(\mathscr{F}=\{\varnothing,A,\bar{A},\Omega\}\),我们关心的只有事件\(A\)是否发生,这样的随机事件称为伯努利试验。伯努利试验是最简单的随机事件,但你将看到,它几乎可以看成是随机世界的“原子事件”,众多的伯努利试验在一起,就能够变幻出无穷的可能。为了便于讨论,以下记\(P(A)=p,P(\bar{A})=q\),它也是伯努利试验的概率分布。
单个伯努利试验是平凡的,接下来研究可数个独立伯努利试验组成的随机事件,研究的方法是从空间和时间两个角度着手。至于空间角度,就是\(n\)次伯努利试验中\(A\)发生的次数\(k\),这是大家熟悉的二项分布(1),因为它是二项式\((ps+q)^n\)中\(s^k\)的系数。利用简单的比较法可知,二项分布在\([0,n]\)上先增后减,并且在\([(n+1)p]\)上取得最大值(中心项)。
\[b(k;n,p)=\binom{n}{k}p^kq^{n-k}\tag{1}\]
再从时间角度看,考察\(A\)第一次发生在第\(k\)次试验的概率,容易算得是式(2)左的等比数列,故它也被称为几何分布。几何分布是描述时间的随机变量,由于每次伯努利试验是独立的,可以想象已经过去的时间\(m\)并不会影响还需等待的时间\(k\)。即几何分布满足式(2)右的性质,它被称为几何分布的无记忆性。这是几何分布的核心性质,还可以证明,满足无记忆性的离散分布只有几何分布。
\[g(k;p)=q^{k-1}p;\;\;P\{\xi=m+k|\xi>m\}=P\{\xi=k\}\tag{2}\]
继而再来看\(A\)第\(r\)次发生的时间,容易知道它是式(3)左的帕斯卡分布。根据几何分布的无记忆性,容易想到,帕斯卡分布的随机变量\(\eta\)其实就是\(r\)个独立同分布的几何分布之和,即\(\eta=\xi_1+\cdots+\xi_r\)。另外,如果以失败次数\(\zeta=\eta-r\)为随机变量,可以得到一个更简单的式(3)右,它称为负二项分布,本质上和帕斯卡分布是一样的。
\[f(k;r,p)=\binom{k-1}{r-1}p^rq^{k-r};\;\;Nb(l;r,p)=\binom{-r}{l}p^r(-q)^l\tag{3}\]
1.2 泊松过程
由伯努利试验生成的都是离散分布,试图以此研究连续分布看似是不可能的。观察二项分布(1),随着\(n\)的增大,分布的中心项向右移动,且整个分布越来越平坦。为了研究极限场景的现象,我们可以做如下大胆想象:中心项向右移动的同时,将数轴反比例压缩。极限情况下,伯努利试验稠密地发生在数轴上,且中心项在固定的位置\(np\to \lambda\)。
想象中我们得到了一个“连续”的二项分布,下面从数学上描述这个分布。要注意这里有关键的条件\(np_n\to \lambda\),\(\lambda\)是连续场景下“原子事件”发生概率的参数。将二项分布改成式(4),分析其极限便得到式(5)的泊松分布。泊松分布不仅可以作为二项分布的近似(当然要求\(np\)大小合适),它自身就是连续场合下的“原子分布”。
\[b(k;n,p_n)=\dfrac{\lambda^k}{k!}(1-\dfrac{1}{n})\cdots(1-\dfrac{k-1}{n})(1-\dfrac{\lambda}{n})^{n-k}\tag{4}\]
\[b(k;n,p_n)\to b(k;\lambda)=\dfrac{\lambda^k}{k!}e^{-\lambda}\tag{5}\]
泊松分布的“原子性”可以这样理解:事件按照一定概率随时可能发生,但任何两次发生都相互独立。严格来说,这样一种连续过程被称为泊松过程,现实中泊松分布应该是泊松过程某个时间段内事件发生次数的分布。仔细品味泊松过程的含义,它是非常广泛的随机过程,比如公交站台的到客事件、服务台的呼叫事件、网站访问事件等,随时发生而互相独立。
弄清了泊松过程和泊松分布的关系,我们可以知道针对同一泊松过程,泊松分布的参数\(\lambda\)应该与时间段\(t\)成正比。为此,可由式(6)来完整描述某个泊松过程,并且它有性质(7)。反之还可以证明,如果随机过程满足式(7),它必然是泊松过程,证明需要用到一些分析学的技巧,请参考教材。另外,随机过程的概念以后我们会有专门课程,这里先感受一下它的存在。
\[P_k(t)=\dfrac{(\lambda t)^k}{k!}e^{-\lambda t}\tag{6}\]
\[P_k(t_1+t_2)=P_k(t_1)P_0(t_2)+P_{k-1}(t_1)P_1(t_2)+\cdots+P_0(t_1)P_k(t_2)\tag{7}\]
同样,可以从时间角度考察泊松过程,比如求事件第一次的时间分布,按照定义,第一次发生在\(t
\[p(x)=\lambda e^{-\lambda x};\;\;P\{\tau\geqslant s+t|\tau\geqslant s\}=P\{\tau\geqslant t\}\tag{8}\]
同样的方法,可以求得事件第\(r\)次发生时间的分布密度是式(9),它叫做埃尔朗分布。埃尔朗分布的随机变量\(W_r\),也是\(r\)个独立同分布的指数分布之和\(W_r=\tau_1+\cdots+\tau_r\)。
\[p(x)=\dfrac{\lambda^r}{(r-1)!}x^{r-1}e^{-\lambda x},\;\;(x>0)\tag{9}\]
2. 问题举例
数学学习的核心应该在对基本问题的讨论,但适量的习题也是必须的,习题不光能加深概念的理解,好的题目非常锻炼综合思考能力。这里列举一些我知道的概率问题,详加思考体会其中的趣味。
2.1 三门问题
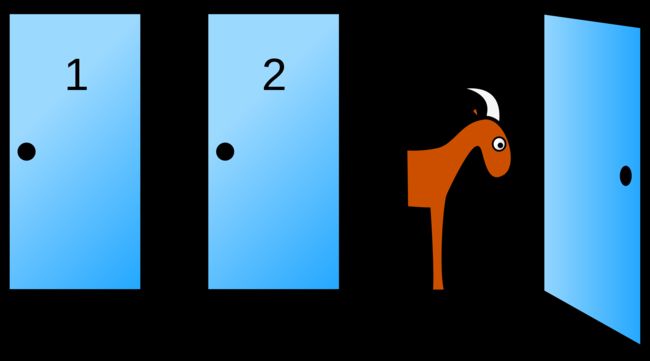
“三门问题”大家都不陌生,因其题干简单但答案颇具争议,而为各种科普文章所津津乐道。争议本身正说明了,当问题复杂到一定程度,直觉的理解力和表达力都会遇到困难,各种混沌和诡辩都会混入其中。这时候就需要模型抽象和理论系统,剥离开表面的障碍,分析问题的本质。好了废话少说,先来看题干:三扇门后面分别是一辆汽车和两头山羊,你的目的是选出汽车那扇门。你先选择一扇门但不打开,而这时主持人在剩下的门中打开有山羊的一扇(如果两扇都是山羊则随便打开一扇),这时问你要不要换选另一扇门?
任何概率问题都要从选取样本空间开始,每个样本点要是一种可能的状态,并且最好是等概率的(便于计算)。这个问题的状态可以分得很细,从开始三扇门的布局,到你的选择,再到主持人的选择,这三层状态得到的样本空间比较多。其实考虑到对称性,只需分为三种等概率的可能:一开始选中的是车、第一只羊、第二只羊,后两种合并之后就变成概率空间\(\{\dfrac{1}{3},\dfrac{2}{3}\}\)。然后就是两个概率问题,第一个是不换得到车的概率,第二个是换得到车的概率。
面对这么简单的概率空间,答案已经非常明显,不换和换得到车的概率分别就是\(\dfrac{1}{3}\)和\(\dfrac{2}{3}\)。任何思辨都会陷入对局部问题的讨论,而脱离样本空间本身,这也正是本体的趣味所在。与此类似的还有一题,你可以考虑一下:有三张卡片,它们的两面分别是:黑黑、白白、黑白,随机取一张并仅看一面,如果看到的是黑,它反面是白的概率是多少?
2.2 分赌注问题
分赌注问题的确是一个比较正统的概率论问题,它也被看做是概率论诞生的事件。问题描述很简单,说甲乙两人下赌注,然后反复进行双人赌局,约定谁先赢\(t\)局者获胜。显然,有限赌局后一定可以分出胜负,有趣的问题是:赌局在甲胜\(r\)局、乙胜\(s\)局后被迫中止,那赌注该如何分配?一种最简单粗暴的方法就是按照\(r:s\)的比例关系分配,这种方法只是符合了含糊的直觉,完全经不起推敲。
稍加思考后你便会发现,这是一个重复的伯努利试验,而问题等价于:甲再赢\(m=t-r\)局或乙再赢\(n=t-s\)局先发生的概率。这两个概率是互补的,以下求甲赢的概率。但在此之前,需要先给出甲每局能赢的概率\(p\),一般以\(\dfrac{1}{2}\)较为公平。当然也可以设定为\(\dfrac{r}{r+s}\),这个由当事人确定,与概率论无关。
模型确定后,问题也就简单了,式(10)分别从三个角度得出答案,它们其实是相等的:(1)根据乙赢的次数或总次数;(2)根据乙赢时甲赢的次数;(3)接下来的\(m+n-1\)局里甲胜的局数。
\[\sum\limits_{k=0}^{n-1}\binom{m+k-1}{k}p^mq^k;\;\;\sum\limits_{k=m}^{\infty}\binom{n+k-1}{k}p^kq^n;\;\;\sum\limits_{k=m}^{m+n-1}\binom{m+n-1}{k}p^kq^{m+n-k-1}\tag{10}\]
2.3 随机游动问题
重复伯努利试验还有一种常见的变形,即把事件发生和不发生对应到数轴上的左右移动单位距离,而关注的则是游离的位置。这样的问题叫质点的随机游动问题,它也可以扩展到平面或空间,用来研究布朗运动。现在假设质点在数轴上每次移动单位距离,且向正(负)方向的移动概率是\(p\)(\(q\)),关注的则是\(t=n\)时刻质点的位置\(S_n\)。
当数轴上无障碍时,问题比较平凡,首先位置\(S_n\)一定与\(n\)有相同的奇偶性,且在一定的范围之内。然后可以算出质点左右移动的次数,并得到概率分布(11)。当数轴上设立了一些吸盘后,质点落在吸盘上就再也不能游动,这时的问题会变得有趣得多。但要提醒一点,游动可能是无限次的,在计算一些概率之前,最好先论证它的存在性。
\[P\{S_n=k\}=\binom{n}{\frac{n+k}{2}}p^{\frac{n+k}{2}}q^{\frac{n-k}{2}}\tag{11}\]
第一种情况是在质点两侧都有吸盘,比如质点最初在\(a\)点,吸盘在0和\(a+b\)点。问题是,质点是不是一定会被吸住?被左右吸住概率分别是多少?假定初始位置在\(n\)时,被左(右)边的吸盘吸住的概率是\(p_n\)(\(q_n\)),容易得到式(12)的递推式和边界条件。不难由此求得式(13),同样可以求得\(q_n\),且可以验证被吸住的概率为\(1\)。
\[p_n=pp_{n-1}+qp_{n+1},\;\;(p_0=1,p_{a+b}=0)\tag{12}\]
\[p_n=1-\dfrac{n}{a+b},\;(p=q);\;\;p_n=\dfrac{1-\left(p/q\right)^b}{1-\left(p/q\right)^{a+b}},\;(p\ne q)\tag{13}\]
当\(b\to\infty\)的时候,可以把结论推广到只有一侧有吸盘的问题,它的结论是式(14)。如果你觉得不严格,也可以通过递推式和边界条件计算,只不过目前只有一个边界值。幸好有一个很巧妙的方法能求得\(p_1\),请仔细品味。首先质点只能在奇数时间被吸住,而且可以算得第\(2n+1\)次被吸住的概率为\(p^{n+1}q^nC_n\),其中\(C_n\)是卡特兰数。所以\(p_1\)可以写成式(15),利用卡特兰数的卷积性质,可以考虑将\(p_1\)与自身相乘,整理后得到(16),解方程也能得到式(14)。
\[p_n=1,\;(p\leqslant q);\;\;p_n=\frac{q}{p},\;(p>q)\tag{14}\]
\[p_1=\sum\limits_{k=1}^{\infty}p^{k+1}q^kC_k\tag{15}\]
\[S^2=S-mC_1,\;\;(S=p_1/p,\,m=pq)\tag{16}\]
随机游动问题其实来自于著名的“赌徒输光问题”,从结论中你也可以体会到,初始值的大小对结果的影响是大于每局赢的概率的。
2.4 互质随机数
正整数集是无限集,如果有人提出:随机取一个正整数,这可能吗?如果可能它是\(1\)的概率是多少?由于不懂测度论,我不敢对这个问题妄下结论,但要是把问题改一下,则是能理解的:随机取一个正整数,考察是否是\(p\)的倍数,易知事件的概率是\(\dfrac{1}{p}\)。这个结论对任何正整数\(p\)都成立,当然也适用于质数\(p_1,p_2\)。由于质数之间互质,故\(p_1\)的倍数\(np_1\)整除\(p_2\)的概率还是\(\dfrac{1}{p_2}\)。也就是说“\(p_1\)的倍数”与“\(p_2\)的倍数”是独立事件,更进一步还有:与不同质数互质的事件之间是相互独立的。
既然与不同质数互质相互独立,则与所有质数\(\{p_1,p_2,\cdots\}\)互质的概率是\(P=\prod\limits_i(1-\dfrac{1}{p_i})\)。为了求得\(P\),可以利用\(\frac{1}{1-x}=1+x+x^2+\cdots\),以及所有正整数的质数分解特点,得到式(17)。从而\(P=0\),它表明随机正整数是质数的概率为\(0\)。
\[P^{-1}=\prod_i\dfrac{1}{(1-1/p_i)}=\prod_i\sum_{j=0}^{\infty}\dfrac{1}{p_i^j}=\sum_{n=1}^{\infty}\dfrac{1}{n}=\infty\tag{17}\]
上式的得到调和级数的那一步很关键,它也是数论中的常用等式。继续以上讨论,如果先后随机取两个正整数,它们有公因数\(p\)的概率是\(\dfrac{1}{p^2}\)。类似地,也能证明:对质数\(p_1,p_2\),两个数“都是\(p_1\)的倍数”与“都是\(p_2\)的倍数”是独立事件。这样我们就可以用相同的方法,计算两个随机正整数互素的概率\(P\),从式(18)便知\(P=\dfrac{6}{\pi^2}\)。
\[P^{-1}=\prod_i\dfrac{1}{(1-1/p_i^2)}=\sum_{n=1}^{\infty}\dfrac{1}{n^2}=\dfrac{\pi^2}{6}\tag{18}\]