上一篇中我们详细介绍推导了主成分分析法的原理,并基于Python通过自编函数实现了挑选主成分的过程,而在Python与R中都有比较成熟的主成分分析函数,本篇我们就对这些方法进行介绍:
R
在R的基础函数中就有主成分分析法的实现函数princomp(),其主要参数如下:
data:要进行主成分分析的目标数据集,数据框形式,行代表样本,列代表变量
cor:逻辑型变量,控制是否使用相关系数进行主成分分析
scores:逻辑型变量,控制是否计算每个主成分的得分
我们使用了R中自带的数据集USJudgeRating来进行演示,这是一个包含43个样本,12个连续型实自变量的数据集,适合来演示PCA,这里我们在其自带方法的基础上,使用自编函数来对训练后的数据进行一步到位的,基于用户自定义贡献率阈值(默认0.8)来生成所需主成分值,具体过程如下:
> rm(list=ls()) > > #载入律师评价数据 > data(USJudgeRatings) > data <- USJudgeRatings > > #对律师评价数据进行主成分分析,这里设置使用相关系数进行主成分分析 > data.pr <- princomp(data,cor=T,scores=T) > > #自定义目标主成分值生成函数 > My_Choose <- function(data.pr,a=0.8){ + contribute <- data.pr$sdev^2/sum(data.pr$sdev^2) + c <- 0 + i <- 0 + #根据累计贡献率挑选所需最少的主成分 + while(c<=a){ + i <- i + 1 + c <- c + contribute[i] + } + cat('达到要求,已采纳的主成分累计贡献率达到:','\n',round(c,4),'\n') + return(predict(data.pr)[,1:i]) + } > > #显示主成分分析的结果,以及因子载荷 > summary(data.pr, loadings = T) Importance of components: Comp.1 Comp.2 Comp.3 Standard deviation 3.1833165 1.05078398 0.5769763 Proportion of Variance 0.8444586 0.09201225 0.0277418 Cumulative Proportion 0.8444586 0.93647089 0.9642127 Comp.4 Comp.5 Comp.6 Standard deviation 0.50383231 0.290607615 0.193095982 Proportion of Variance 0.02115392 0.007037732 0.003107172 Cumulative Proportion 0.98536661 0.992404341 0.995511513 Comp.7 Comp.8 Comp.9 Standard deviation 0.140295449 0.124158319 0.0885069038 Proportion of Variance 0.001640234 0.001284607 0.0006527893 Cumulative Proportion 0.997151747 0.998436354 0.9990891437 Comp.10 Comp.11 Comp.12 Standard deviation 0.0749114592 0.0570804224 0.0453913429 Proportion of Variance 0.0004676439 0.0002715146 0.0001716978 Cumulative Proportion 0.9995567876 0.9998283022 1.0000000000 Loadings: Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8 CONT 0.933 -0.335 INTG -0.289 -0.182 -0.549 -0.174 0.370 -0.450 0.334 DMNR -0.287 -0.198 -0.556 0.124 0.229 -0.395 0.467 -0.247 DILG -0.304 0.164 -0.321 0.302 0.599 0.210 -0.355 CFMG -0.303 0.168 0.207 0.448 0.247 0.714 DECI -0.302 0.128 0.298 0.424 -0.393 -0.536 -0.302 PREP -0.309 0.152 -0.214 -0.203 0.335 -0.154 FAMI -0.307 0.195 -0.201 -0.507 -0.102 ORAL -0.313 -0.246 -0.150 WRIT -0.311 -0.137 -0.306 -0.238 0.126 PHYS -0.281 0.154 0.841 -0.118 0.299 RTEN -0.310 -0.173 0.184 -0.256 -0.221 Comp.9 Comp.10 Comp.11 Comp.12 CONT INTG -0.275 -0.109 -0.113 DMNR -0.199 0.134 DILG 0.383 CFMG 0.143 0.166 DECI -0.258 -0.128 PREP -0.109 -0.680 -0.319 0.273 FAMI -0.223 0.573 -0.422 ORAL 0.300 0.256 -0.639 -0.494 WRIT 0.475 0.696 PHYS -0.266 RTEN 0.756 -0.250 0.286 > > #保存主成分数据 > (pca_data <- My_Choose(data.pr,a=0.9)) 达到要求,已采纳的主成分累计贡献率达到: 0.9365 Comp.1 Comp.2 AARONSON,L.H. 0.59268305 -1.834557041 ALEXANDER,J.M. -2.40817832 -0.878164524 ARMENTANO,A.J. -0.22780349 -0.302316250 BERDON,R.I. -3.66071616 -0.596342199 BRACKEN,J.J. 6.95244952 0.137356050 BURNS,E.B. -2.47442074 -1.422422886 CALLAHAN,R.J. -3.93743704 3.147711145 COHEN,S.S. 8.09307094 -0.271058974 DALY,J.J. -3.70295623 -0.146659161 DANNEHY,J.F. -1.06028925 1.149046170 DEAN,H.H. 0.34108279 -0.470502584 DEVITA,H.J. 1.45772527 -1.232794755 DRISCOLL,P.J. 0.67688211 -1.297855808 GRILLO,A.E. 3.26409534 -0.566023927 HADDEN,W.L.JR. -1.36896588 -0.848756359 HAMILL,E.C. 0.45009339 -0.182461748 HEALEY.A.H. 2.93209773 0.383887639 HULL,T.C. 0.72643742 0.463364335 LEVINE,I. -0.64887947 0.904423859 LEVISTER,R.L. 4.40757580 2.444558329 MARTIN,L.F. 1.84009523 -0.801922043 MCGRATH,J.F. 3.15606059 0.118968056 MIGNONE,A.F. 6.42980257 -1.452770363 MISSAL,H.M. 0.08315548 -1.483307990 MULVEY,H.M. -3.39121775 0.132351096 NARUK,H.J. -4.60271493 0.479764153 O'BRIEN,F.J. -1.51784742 -0.427971456 O'SULLIVAN,T.J. -3.51102566 0.001182987 PASKEY,L. -1.91559427 0.246170053 RUBINOW,J.E. -4.83537434 -0.448069023 SADEN.G.A. -1.11213340 -0.344165889 SATANIELLO,A.G. -0.54875827 1.022509509 SHEA,D.M. -2.61362018 -0.399509080 SHEA,J.F.JR. -3.63917622 -0.162216363 SIDOR,W.J. 6.94389214 0.330376531 SPEZIALE,J.A. -2.04961153 1.193213351 SPONZO,M.J. -1.22081130 -0.531924504 STAPLETON,J.F. -0.72842414 -0.914724377 TESTO,R.J. 2.13120556 0.949624029 TIERNEY,W.L.JR. -1.36785124 1.100438878 WALL,R.A. 2.61916318 1.926895688 WRIGHT,D.B. -1.48026785 -0.556116054 ZARRILLI,K.J. 0.92650698 1.440771500
在得到累计贡献率高达0.9365的两个主成分之后,我们将主成分降维前后的数据的相关系数矩阵进行比较:
> #降维前 > cor(data) CONT INTG DMNR DILG CFMG CONT 1.00000000 -0.1331909 -0.1536885 0.0123920 0.1369123 INTG -0.13319089 1.0000000 0.9646153 0.8715111 0.8140858 DMNR -0.15368853 0.9646153 1.0000000 0.8368510 0.8133582 DILG 0.01239200 0.8715111 0.8368510 1.0000000 0.9587988 CFMG 0.13691230 0.8140858 0.8133582 0.9587988 1.0000000 DECI 0.08653823 0.8028464 0.8041168 0.9561661 0.9811359 PREP 0.01146921 0.8777965 0.8558175 0.9785684 0.9579140 FAMI -0.02563656 0.8688580 0.8412415 0.9573634 0.9354684 ORAL -0.01199681 0.9113992 0.9067729 0.9544758 0.9505657 WRIT -0.04381025 0.9088347 0.8930611 0.9592503 0.9422470 PHYS 0.05424827 0.7419360 0.7886804 0.8129211 0.8794874 RTEN -0.03364343 0.9372632 0.9437002 0.9299652 0.9270827 DECI PREP FAMI ORAL CONT 0.08653823 0.01146921 -0.02563656 -0.01199681 INTG 0.80284636 0.87779650 0.86885798 0.91139915 DMNR 0.80411683 0.85581749 0.84124150 0.90677295 DILG 0.95616608 0.97856839 0.95736345 0.95447583 CFMG 0.98113590 0.95791402 0.93546838 0.95056567 DECI 1.00000000 0.95708831 0.94280452 0.94825640 PREP 0.95708831 1.00000000 0.98986345 0.98310045 FAMI 0.94280452 0.98986345 1.00000000 0.98133905 ORAL 0.94825640 0.98310045 0.98133905 1.00000000 WRIT 0.94610093 0.98679918 0.99069557 0.99342943 PHYS 0.87176277 0.84867350 0.84374436 0.89116392 RTEN 0.92499241 0.95029259 0.94164495 0.98213227 WRIT PHYS RTEN CONT -0.04381025 0.05424827 -0.03364343 INTG 0.90883469 0.74193597 0.93726315 DMNR 0.89306109 0.78868038 0.94370017 DILG 0.95925032 0.81292115 0.92996523 CFMG 0.94224697 0.87948744 0.92708271 DECI 0.94610093 0.87176277 0.92499241 PREP 0.98679918 0.84867350 0.95029259 FAMI 0.99069557 0.84374436 0.94164495 ORAL 0.99342943 0.89116392 0.98213227 WRIT 1.00000000 0.85594002 0.96755639 PHYS 0.85594002 1.00000000 0.90654782 RTEN 0.96755639 0.90654782 1.00000000 > #降维后 > cor(pca_data) Comp.1 Comp.2 Comp.1 1.000000e+00 2.161808e-16 Comp.2 2.161808e-16 1.000000e+00
可以看出,降维后两个主成分之间的相关系数非常低,可以说它们几乎正交,说明主成分的结果非常有效:
Python
我们使用sklearn.decomposition中的PCA来实现主成分降维,其主要参数如下:
n_components:这个参数可以帮我们指定希望PCA降维后的特征维度数目。最常用的做法是直接指定降维到的维度数目,此时n_components是一个大于等于1的整数。当然,我们也可以指定主成分的累计贡献率阈值,让PCA类自己去根据样本特征方差来决定降维到的维度数,此时n_components是一个(0,1]之间的数。当然,我们还可以将参数设置为"mle", 此时PCA类会用MLE算法根据特征的方差分布情况自己去选择一定数量的主成分特征来降维。我们也可以用默认值,即不输入n_components,此时n_components=min(样本数,特征数)
whiten :判断是否进行白化。所谓白化,就是对降维后的数据的每个特征进行归一化,让方差都为1。对于PCA降维本身来说,一般不需要白化。如果你PCA降维后有后续的数据处理,可以考虑白化。默认值是False,即不进行白化。
svd_solver:即指定奇异值分解SVD的方法,由于特征分解是奇异值分解SVD的一个特例,一般的PCA库都是基于SVD实现的。有4个可以选择的值:{‘auto’, ‘full’, ‘arpack’, ‘randomized’}。randomized一般适用于数据量大,数据维度多同时主成分数目比例又较低的PCA降维,它使用了一些加快SVD的随机算法。 full则是传统意义上的SVD,使用了scipy库对应的实现。arpack和randomized的适用场景类似,区别是randomized使用的是scikit-learn自己的SVD实现,而arpack直接使用了scipy库的sparse SVD实现。默认是auto,即PCA类会自己去在前面讲到的三种算法里面去权衡,选择一个合适的SVD算法来降维。一般来说,使用默认值就够了。
除了这些输入参数外,有两个PCA类的输出值得关注。第一个是explained_variance_,它代表降维后的各主成分的方差值。方差值越大,则说明越是重要的主成分。第二个是explained_variance_ratio_,它代表降维后的各主成分的方差值占总方差值的比例,这个比例越大,则越是重要的主成分。
我们选用datasets中自带的wine数据集作为演示数据,关于这个数据集可以参考前一篇的介绍,具体过程如下:
from sklearn.decomposition import PCA from sklearn import datasets import numpy as np '''载入数据''' X,y = datasets.load_wine(return_X_y=True) '''显示待转换数据的形状''' print(X.shape) '''初始化PCA模型,这里选择希望从13个原始变量中产出三个主成分''' pca = PCA(n_components=3) '''将X导入设定好的模型中''' pca.fit(X) '''打印产出的主成分对应的方差贡献率''' print(pca.explained_variance_ratio_) '''打印产出的主成分对应的方差''' print(pca.explained_variance_) '''将模型产出的目标主成分保存''' X_new = pca.fit_transform(X)
原始数据的形状以及得到的主成分的各自的方差贡献率、方差如下:
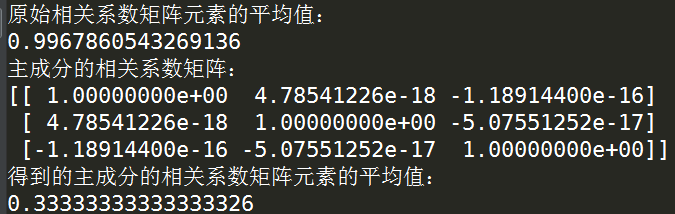
下面计算原始数据的相关系数矩阵中元素的平均值与得到的主成分进行对比:
'''计算原始数据相关系数矩阵的平均值''' print('原始相关系数矩阵元素的平均值:'+'\n'+str(np.mean(np.corrcoef(X)))) '''计算保留的主成分之间的相关系数''' print('主成分的相关系数矩阵:'+'\n'+str(np.corrcoef(X_new.T))) '''计算主成分相关系数矩阵的平均值''' print('得到的主成分的相关系数矩阵元素的平均值:'+'\n'+str(np.mean(np.corrcoef(X_new.T))))
比较结果如下:
可以看出,经过主成分分析,我们得到了比较好的降维数据,这又一次说明了主成分分析的重要性;
以上就是关于Python和R中主成分分析基础降维功能的介绍,如有不正确之处望指出。