转载请标明出处,谢谢!
https://www.jianshu.com/p/176b0b892591
关联文章
排序 https://www.jianshu.com/p/176b0b892591
栈和队列 https://www.jianshu.com/p/8cb602ef4e21
顺序表、单双链表 https://www.jianshu.com/p/3aeb5998e79e
二叉树 https://www.jianshu.com/p/de829eab944c
图论 https://www.jianshu.com/p/cf03e51a3ca2
冒泡排序和选择排序,适合个位数的排序
冒泡排序(Bubble Sort)
一种计算机科学领域的较简单的排序算法。
它重复地走访过要排序的元素列,依次比较两个相邻的元素,如果他们的顺序(如从大到小、首字母从A到Z)错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换,也就是说该元素已经排序完成。
这个算法的名字由来是因为越大的元素会经由交换慢慢“浮”到数列的顶端(升序或降序排列),就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样,故名“冒泡排序”。
冒泡排序简单的讲就是相邻的两个数字对比,大的数往后推。
private void bubbleSort(int[] array){
for (int i = 0; i array[i+1]){
int temp = array[i];
array[i] = array[i+1];
array[i+1] = temp;
}
}
print(array);
}
输出的结果是:
第一轮下来 已经把最大的数字9往后推到最后一位。 接下来就要比较1 3 5 2 ->1 3 2 5 然后是1 3 2 所以按照这个思路再最外面加一个for循环就可以将数组排序
private void bubbleSort(int[] array){
for (int j = 0; j array[i+1]){
int temp = array[i];
array[i] = array[i+1];
array[i+1] = temp;
}
}
}
print(array);
}
我们看下,这是最基本的冒泡排序写法。那么我们看下他的时间复杂度是多少?冒泡排序的时间复杂度是O(n²)。这是冒泡排序的最差时间复杂度。那么他有没有优化的方案呢?
有! 我们可以假设下 如果一开始的数组数据就是从小到大排序好的呢? 那么真正的有效代码时间复杂度是O(n),因为if语句根本就走不进去。 我们看下代码。
@Test
public void test() {
int[] array = new int[]{1, 2, 3, 4, 5};
bubbleSort(array);
}
private void bubbleSort(int[] array) {
for (int j = 0; j < array.length - 1; j++) {
boolean flag = true;
for (int i = 0; i < array.length - 1 - j; i++) {
if (array[i] > array[i + 1]) {
int temp = array[i];
array[i] = array[i + 1];
array[i + 1] = temp;
flag = false;
}
}
if (flag) {
break;
}
}
print(array);
}
选择排序
一种简单直观的排序算法。它的工作原理很容易理解:初始时在序列中找到最小(大)元素,放到序列的起始位置作为已排序序列;然后,再从剩余未排序元素中继续寻找最小(大)元素,放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
注意选择排序与冒泡排序的区别:冒泡排序通过依次交换相邻两个顺序不合法的元素位置,从而将当前最小(大)元素放到合适的位置;而选择排序每遍历一次都记住了当前最小(大)元素的位置,最后仅需一次交换操作即可将其放到合适的位置。
先排第一次,首先将第一个数字固定然后和后面一个数字3对比 如果4>3就将3的角标赋值给index,然后对换数字,以此类推,我们看下结果:
private void selectionSort() {
int[] array = new int[]{4, 3, 9, 5, 2};
int index = 0;
for (int i = 0 + 1; i < array.length; i++) {
/*如果后者大于第一个数 index重新赋值*/
if (array[index] > array[i]) {
index = i;
}
/*替换两个数*/
int temp = array[index];
array[index] = array[0];
array[0] = temp;
}
print(array);
}
按照这样的思路,再最外层加上一个循环进行排序:
private void selectionSort() {
int[] array = new int[]{4, 3, 9, 5, 2};
for (int j = 0; j < array.length - 1; j++) {
int index = j;
for (int i = j + 1; i < array.length; i++) {
/*如果后者大于第一个数 index重新赋值*/
if (array[index] > array[i]) {
index = i;
}
/*替换两个数*/
int temp = array[index];
array[index] = array[j];
array[j] = temp;
}
}
print(array);
}
那么这个算法也有优化方案吗?有!
private void selectionSort() {
int[] array = new int[]{4, 3, 9, 5, 2};
for (int j = 0; j < array.length - 1; j++) {
int index = j;
for (int i = j + 1; i < array.length; i++) {
/*如果后者大于第一个数 index重新赋值*/
if (array[index] > array[i]) {
index = i;
}
/*替换两个数*/
if (index != j) {//如果已经是最小的,就不需要替换
int temp = array[index];
array[index] = array[j];
array[j] = temp;
}
}
}
print(array);
}
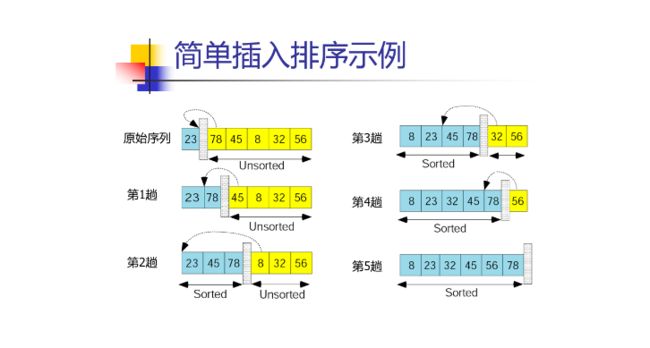
插入排序
插入排序类似整理扑克牌,将每一张牌插到其他已经有序的牌中适当的位置。
插入排序由N-1趟排序组成,对于P=1到N-1趟,插入排序保证从位置0到位置P上的元素为已排序状态。
简单的说,就是插入排序总共需要排序N-1趟,从index为1开始,讲该位置上的元素与之前的元素比较,放入合适的位置,这样循环下来之后,即为有序数组。
为了看清原理,先模拟三个数据
@Test
public void test() {
int[] array = new int[]{2, 4, 1};
insertSort(array);
print(array);
}
//直接插入排序
public void insertSort(int[] array) {
int j = 2;
int target = array[j];
while (j > 0 && target < array[j - 1]) {
array[j] = array[j - 1];
j--;
}
array[j] = target;
}
public void print(int[] array) {
for (int i = 0; i < array.length; i++) {
System.out.println(array[i]);
}
}
分析: j=2, target = array[j] = 1;
如果1<4 则替换,然后j = 1, 再替换。几轮下来 1就跑到最前面 输出的结果是 1,2,4.
完整代码:
//直接插入排序
public void insertSort(int[] array) {
for (int i = 0; i 0 && target < array[j - 1]) {
array[j] = array[j - 1];
j--;
}
array[j] = target;
}
}
希尔排序
希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因D.L.Shell于1959年提出而得名。
该方法实质上是一种分组插入方法
比较相隔较远距离(称为增量)的数,使得数移动时能跨过多个元素,则进行一次比较就可能消除多个元素交换。D.L.shell于1959年在以他名字命名的排序算法中实现了这一思想。算法先将要排序的一组数按某个增量d分成若干组,每组中记录的下标相差d.对每组中全部元素进行排序,然后再用一个较小的增量对它进行,在每组中再进行排序。当增量减到1时,整个要排序的数被分成一组,排序完成。
一般的初次取序列的一半为增量,以后每次减半,直到增量为1。
给定实例的shell排序的排序过程
假设待排序文件有10个记录,其关键字分别是:
49,38,65,97,76,13,27,49,55,04。
增量序列的取值依次为:
5,2,1
代码:
改进刚刚的插入排序
@Test
public void test() {
int[] array = new int[]{2, 4, 1, 44, 3, 22, 7, 8, 9, 444};
//insertSort(array);
shellSort(array, 5);
shellSort(array, 2);
shellSort(array, 1);
print(array);
}
//希尔排序
public void shellSort(int[] array, int step) {
for (int k = 0; k < step; k++) {
for (int i = k + step; i < array.length; i += step) {
int j = i;
int target = array[j];
while (j > step - 1 && target < array[j - step]) {
array[j] = array[j - step];
j -= step;
}
array[j] = target;
}
}
}
堆排序
堆排序(英语:Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
堆排序的过程:
1。从最后一个非叶子节点开始,每三个节点做一次大小比较,最小的做根
如果移动过程中如果子树上的顺序被破坏了,子树上重新调整三个节点的位置
2。取走整个树的根节点,把最后一个叶子做为根节点
3。重复1和2,直到所有节点被取走了
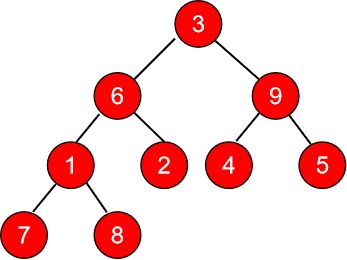
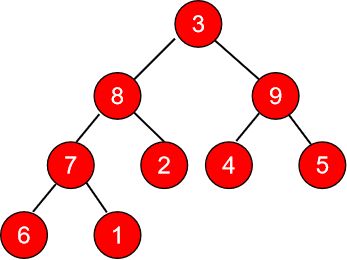
举个例子说明下:有一个数组 3、6、9、1、2、4、5、7、8
用完全二叉树表示
根据堆排序过程
先从1开始
然后从9开始
不用操作。
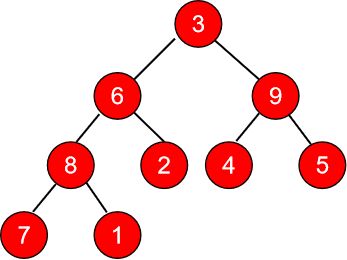
然后操作6
操作完6 发现 做左边的三个节点需要调整:
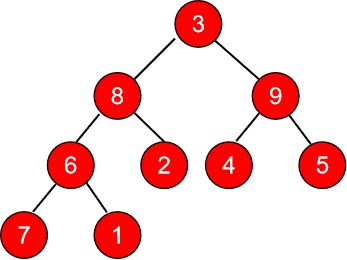
操作3
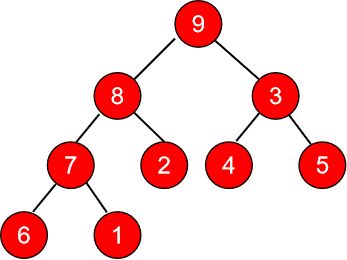
右小角需要调整:
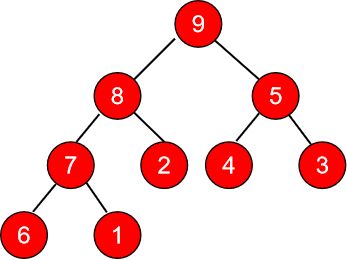
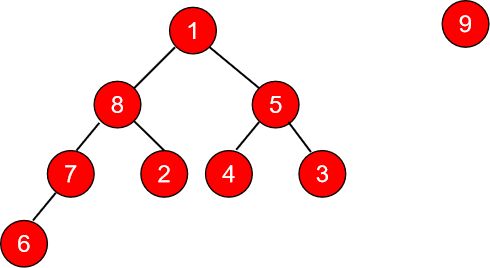
上图就是调整后的二叉树。我们发现9已经被推到了最上面。接着取出9,将最后一个叶子节点1作为根节点
然后重复上面的操作。
代码:
@Test
public void test(){
int[] array=new int[]{2,3,4,5,6,7,1,8,9};
heapSort(array,array.length);
for (int i = 0; i < array.length; i++) {
System.out.print(array[i]+" ");
}
}
/**
* 调整堆
*/
void maxHeapify(int array[],int start,int end){
//父亲的位置
int dad=start;
//儿子的位置
int son=dad*2+1;
while(son<=end){//如果子节点下标在可以调整的范围内就一直调整下去
//如果没有右孩子就不用比,有的话,比较两个儿子,选择最大的出来
if(son+1 <= end && array[son]array[son]){
return;
}else{//父亲比儿子小,就要对整个子树进行调整
int temp=array[son];
array[son]=array[dad];
array[dad]=temp;
//递归下一层
dad=son;
son=dad*2+1;
}
}
}
void heapSort(int array[],int len){
//建堆 len/2-1最后一个非叶子节点
for(int i=len/2-1;i>=0;i--){
maxHeapify(array,i,len-1);
}
//排序,根节点和最后一个节点交换
//换完以后,取走根,重新建堆
//len-1 最后一个节点
for(int i=len-1;i>0;i--){
int temp=array[0];
array[0]=array[i];
array[i]=temp;
maxHeapify(array,0,i-1);
}
}
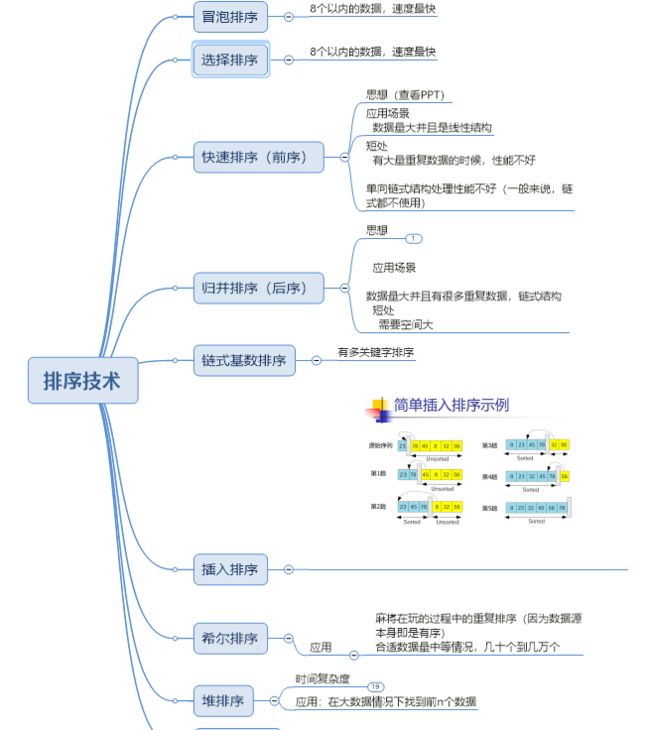
看下八大排序的应用场景