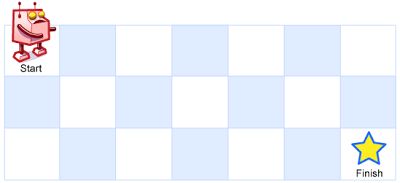
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?
Above is a 3 x 7 grid. How many possible unique paths are there?
Note: m and n will be at most 100.
一刷
题解:
dp的经典问题,每次向右或向下走一步。第一行或者第一列走到头只有一种方法,所以初始化为1,转移方程是dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
思路一,构造m*n的矩阵保存dp[i][j]
Time complexity O(mn), space complexity O(mn)
public class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
for(int i=0; i思路二,由于dp[i][j] = dp[j][i]是对称的,考虑利用这个特点来save space
Time complexity O(mn), space complexity O(n)
public class Solution {
public int uniquePaths(int m, int n) {
if(m<0 || n<0) return 0;
int[] dp = new int[n];
for(int i=0; i