目录
- 网络流算法进阶详解
- 基础知识
- 最大流
- 最小割
- EK算法
- DINIC算法
- 最小费用流
- 进阶
- 无源汇可行流
- 有源汇上下界最大流
- 有源汇上下界最小流
- 一些建图模型
- 最大权闭合子图
- 星际战争
- poj1149
- CQOI2009 跳舞
- 基础知识
网络流算法进阶详解
基础知识
由于之前写过总结,这部分会写的比较简单
最大流
模型就是有很多根管子,从源点流出inf的流,问汇点有多少流量
一个显然的思路是贪心,但是很容易给出反例。
和一道种树的题类似(题目就叫这个?或者叫植树),那道题是贪心取一个点后把它的权值取负并与旁边选了就不能选它的点合并,这样可以达到反悔的效果
那我们建立反向边,在每次流出流量之后,给反向边加上对应的流量,这样就能保证贪心的正确性了。
在保证没有负环时边权改为负数就能跑最小流
最小割
=最大流,需要证三个结论互为逆否命题,之前写的博客有证,此处就不写了
其实记住就行了(
EK算法
每次找一条可以流的增广路,并把这条由源到汇的边集上的流量减去流走的流量
DINIC算法
多路增广,这个算法比较常见,虽然有更优秀的算法,但出题人不会卡
具体实现是先bfs分层,然后dfs流走所有能流的流量,这部分需要看代码实现
#include
#include
#include
#include
#define ll long long
using namespace std;
const int N=201,M=10001;
struct node{
int v,next;ll w;
}edge[M*2];
int top=1,head[N],cur[N];
const ll inf=100909260817ll;
inline void add(int from,int to,int w){
edge[++top].v=to;
edge[top].next=head[from];
head[from]=top;
edge[top].w=w;
}
inline int read(){
char ch=getchar();int x=0;int pos=1;
for(;!isdigit(ch);ch=getchar()) if(ch=='-') pos=0;
for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0';
return pos?x:-x;
}
int n,m,s,t;
int dir=0,level[N];
queueq;
inline int Min(ll a,ll b){
return a>b?b:a;
}
inline int bfs(){
memset(level,-1,sizeof(level));
level[s]=0;q.push(s);
while(!q.empty()){
int now=q.front();q.pop();
for(int i=head[now];i;i=edge[i].next){
int v=edge[i].v;
if(level[v]==-1&&edge[i].w){
level[v]=level[now]+1;
q.push(v);
}
}
}
if(level[t]==-1) return 0;
else return 1;
}
inline ll dfs(int now,ll flow){
if(now==t) return flow;
ll res=flow;
for(int &i=cur[now];i;i=edge[i].next){
int v=edge[i].v;
if(edge[i].w&&level[v]==level[now]+1){
ll k=dfs(v,Min(edge[i].w,res));
res-=k;edge[i].w-=k;edge[i^1].w+=k;
}
if(!res) break;
}
return flow-res;
}
inline ll dinic(){
ll ans=0;
while(bfs()){
memcpy(cur,head,sizeof(head));
ans+=dfs(s,inf);
}
return ans;
}
int main(){
n=read();m=read();s=read();t=read();
for(int i=1;i<=m;i++){
int ui=read(),vi=read(),wi=read();
add(ui,vi,wi);
add(vi,ui,0);
}
printf("%lld",dinic());
return 0;
} 二分图上的复杂度
\(m*min(n^\frac{2}{3},m^\frac{1}{2})\)
最小费用流
此时每根管子的流量有了一个费用。在最大流的情况下,肯定是优先走边权小的,那么此时改变DINIC的访问顺序就行了。具体做法是把bfs换成spfa(可能有负权边,不能用dij),看代码实现吧
#include
#include
#include
#include
#include
#define ll long long
#include
#include
using namespace std;
const int N = 401,M=15001;
struct node{
int u,v,c,w,nex;
}edge[M<<1];
int head[N],top=1;
const int inf = 1926081700;
inline void add(int u,int v,int w,int c){
edge[++top].v=v;edge[top].w=w;edge[top].c=c;edge[top].nex=head[u];head[u]=top;
}
inline int read(){
int x=0,pos=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar()) if(ch=='-') pos=0;
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+ch-'0';
return pos?x:-x;
}
int n,m,maxflow,mincost,dis[N],vis[N],cur[N];
namespace DINIC{
int s,t;
int SPFA(){
queueq; q.push(s);
for(int i=1;i<=n;i++) dis[i]=inf;
dis[s]=0;
while(!q.empty()){
int now=q.front();q.pop();
vis[now]=0;
for(int i=head[now];i;i=edge[i].nex){
int v=edge[i].v;
if(edge[i].w&&dis[now]+edge[i].c 进阶
2020qbxt省选班讲的内容(因为顾及其他人水平主要讲的前面
无源汇可行流
算法思路:
先把每条边强行流上下界流量,具体做法是把每条边的权值赋值成上界减下界,并且记录每个点流出的多还是流入的多(存一个数组\(totflow\)表示流入的流量减去流出的流量,此时由于不平衡,需要平衡流量
新建超级源汇\(S,T\)
\(totflow_i<0\),证明流入的多,需要流向其他的点,此时向 \(S\) 向 \(i\) 连 \(-totflow\) 的边
否则证明流出的多,需要其他的点通过原图给它补流量,此时向 \(i\) 向 \(T\) 连 \(totflow\) 的边
同时记录正权点的权值和 \(sum\)(此时正权点权值和=负权点权值和,因为上面加了 \(w\) 就要减去 \(w\))
从 \(S\) 向 \(T\) 跑 \(DINIC\),如果最大流=sum则可以完全弥补不平衡,则有可行流,每条边的流量则为
下界+容量-流量 = 下界+反向边流量
有源汇上下界最大流
同样是算法思路:
- 向 \(s\) 到 \(t\) 连容量为 \(\inf\) 的边,构造循环流
- 使用无源汇可行流的技巧判断是否有解,注意新建源汇和原来的源汇的区别
- 如有解,在残量网络上从 \(s\) 向 \(t\) 跑 \(DINIC\),最大流即为答案
代码:
#include
#include
#include
#include
#include
const int inf = 192608170;
using namespace std;
int read(){
int x=0,pos=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar()) if(ch=='-') pos=0;
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+ch-'0';
return pos?x:-x;
}
const int N = 441,M=50001;
struct node{
int v,nex,w;
}edge[M];
int head[N],top=1;
int s,t,ns,nt,n,m,totflow[M];
void add(int u,int v,int w){
edge[++top].w=w;edge[top].nex=head[u];edge[top].v=v;head[u]=top;
edge[++top].w=0;edge[top].nex=head[v];edge[top].v=u;head[v]=top;
}
int level[N],cur[N];
int bfs(){
queueq;
memset(level,-1,sizeof(level));
q.push(s);level[s]=0;
while(!q.empty()){
int now=q.front();
q.pop();
for(int i=head[now];i;i=edge[i].nex){
int v=edge[i].v;
if(level[v]==-1&&edge[i].w){
level[v]=level[now]+1;
q.push(v);
}
}
}
return level[t]!=-1;
}
int dfs(int now,int flow){
int res=flow;
if(now==t||flow==0) return flow;
for(int &i=cur[now];i;i=edge[i].nex){
int v=edge[i].v;
if(level[v]==level[now]+1&&edge[i].w){
int nw=dfs(v,min(edge[i].w,res));
res-=nw;edge[i].w-=nw;edge[i^1].w+=nw;
if(!res) break;
}
}
return flow-res;
}
int dinic(int S,int T){
s=S,t=T;
int ans=0;
while(bfs()){
memcpy(cur,head,sizeof(head));
ans+=dfs(s,inf);
}
return ans;
}
int las[N];
void del(int now){
edge[now].w=0;
}
int main(){
n=read(),m=read(),ns=read(),nt=read();
for(int i=1;i<=m;i++){
int u=read(),v=read(),low=read(),up=read();
add(u,v,up-low);
totflow[u]-=low;totflow[v]+=low;
}
int num=top;
int S=n+1,T=n+2,sum=0;
for(int i=1;i<=n;i++){
if(totflow[i]<0) add(i,T,-totflow[i]);
else{
add(S,i,totflow[i]);
sum+=totflow[i];
}
las[i]=top;
}
add(nt,ns,inf);
int ans=0;
if(dinic(S,T)!=sum){
printf("please go home to sleep");return 0;
}else{
ans=edge[top].w;
del(top);del(top-1);
ans+=dinic(ns,nt);
printf("%d",ans);
}
return 0;
} 有源汇上下界最小流
同样地,在可行流的基础上,我们希望总流量最小
那么转化为可行流减去最大的从 \(t\) 到 \(s\) 的流量,跑最大流即可
#include
#include
#include
#include
#include
#define ll long long
const ll inf = 19260817000000ll;
using namespace std;
ll read(){
ll x=0,pos=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar()) if(ch=='-') pos=0;
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+ch-'0';
return pos?x:-x;
}
const ll N = 100031,M=400001;
struct node{
ll v,nex,w;
}edge[M];
ll head[N],top=1;
ll s,t,ns,nt,n,m,totflow[M];
void add(ll u,ll v,ll w){
edge[++top].w=w;edge[top].nex=head[u];edge[top].v=v;head[u]=top;
edge[++top].w=0;edge[top].nex=head[v];edge[top].v=u;head[v]=top;
}
ll level[N],cur[N];
ll bfs(){
queueq;
memset(level,-1,sizeof(level));
q.push(s);level[s]=0;
while(!q.empty()){
ll now=q.front();
q.pop();
for(ll i=head[now];i;i=edge[i].nex){
ll v=edge[i].v;
if(level[v]==-1&&edge[i].w){
level[v]=level[now]+1;
q.push(v);
}
}
}
return level[t]!=-1;
}
ll dfs(ll now,ll flow){
ll res=flow;
if(now==t||flow==0) return flow;
for(ll &i=cur[now];i;i=edge[i].nex){
ll v=edge[i].v;
if(level[v]==level[now]+1&&edge[i].w){
ll nw=dfs(v,min(edge[i].w,res));
res-=nw;edge[i].w-=nw;edge[i^1].w+=nw;
if(!res) break;
}
}
return flow-res;
}
ll dinic(ll S,ll T){
s=S,t=T;
ll ans=0;
while(bfs()){
memcpy(cur,head,sizeof(head));
ans+=dfs(s,inf);
}
return ans;
}
ll las[N];
void del(ll now){
edge[now].w=0;
}
int main(){
n=read(),m=read(),ns=read(),nt=read();
for(ll i=1;i<=m;i++){
ll u=read(),v=read(),low=read(),up=read();
add(u,v,up-low);
totflow[u]-=low;totflow[v]+=low;
}
ll num=top;
ll S=n+1,T=n+2,sum=0;
for(ll i=1;i<=n;i++){
if(totflow[i]<0) add(i,T,-totflow[i]);
else{
add(S,i,totflow[i]);
sum+=totflow[i];
}
las[i]=top;
}
add(nt,ns,inf);
ll ans=0;
if(dinic(S,T)!=sum){
printf("please go home to sleep");return 0;
}else{
ans=edge[top].w;
del(top);del(top-1);
ans-=dinic(nt,ns);
printf("%lld",ans);
}
return 0;
} 一些建图模型
最大权闭合子图
考虑构建一张网络流新图,并增添源汇 \(s\), \(t\)
- 从 s 往所有正权点连边,流量为点权
- 从所有负权点往 t 连边,流量为点权的绝对值
- 所有原图中的边在新图中也相连,流量无穷
- 答案为“原图中正权之和”减“新图最小割”
为什么这样做?
考虑我们要决策舍去的东西,选了一些正权点可能要选一些负权点,我们要决策选不选这些点,这个东西就可以交给最小割处理
- 考虑一个二分图,令左边是正权点,右边是负权点,显然每边之中的连边是不需要割的
- 由于要减去,割正权表示不选正权点,割负权表示选了负权点在闭合图内
- 割保证了 \(s\) 与 \(t\) 不连通,那么选了正权的点(不割左边)就一定要割右边负权的边,表示选了相连接的负权点,保证是一个闭合图,反之亦然
- 决策:可以选择割左边的点,表示不选这个点以及负权后继,否则就选了,用最小割算法决策出最优方案
例题
文理分科
太裸了
寿司餐厅
把花费分开来,设为负值
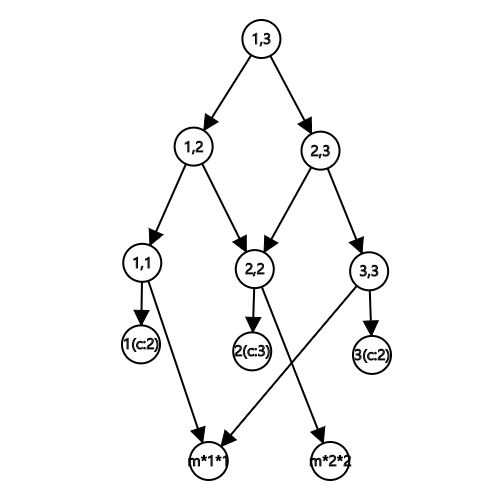
获得的美味度设为正值,像下面那样建图(假设\(a_1=2,a_2=3,a_3=2\)(\(m*1*1\)是种类的代价,x应该不是1,画图的时候没注意))
跑最大权闭合子图就可以了
#include
#include
#include
#include
#include
using namespace std;
int read(){
int x=0,pos=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar()) if(ch=='-') pos=0;
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+ch-'0';
return pos?x:-x;
}
const int N = 6001,M=50001;
const int inf = 192608170;
int n,m,id[N],idc[N],a[N],d[201][201],wd[201][201],s,t,cnt=0,aed[N];
int head[N],cur[N],top=1;
struct node{
int v,nex,w;
}edge[M*2];
inline void add(int u,int v,int w){
edge[++top].v=v;edge[top].nex=head[u];edge[top].w=w;head[u]=top;
edge[++top].v=u;edge[top].nex=head[v];edge[top].w=0;head[v]=top;
}
int vis[N];
inline int bfs(){
memset(vis,-1,sizeof(vis));
queueq;
q.push(s);vis[s]=0;
while(!q.empty()){
int now=q.front();q.pop();
for(register int i=head[now];i;i=edge[i].nex){
int v=edge[i].v;
if(vis[v]==-1&&edge[i].w){
vis[v]=vis[now]+1;
q.push(v);
}
}
}
return vis[t]!=-1;
}
inline int dfs(int now,int flow){
int res=flow;
if(now==t||!flow) return flow;
for(int &i=cur[now];i;i=edge[i].nex){
int v=edge[i].v;
if(vis[v]==vis[now]+1&&edge[i].w){
int nw=dfs(v,min(res,edge[i].w));
edge[i].w-=nw;edge[i^1].w+=nw;res-=nw;
if(!res) break;
}
}
return flow-res;
}
inline int dinic(){
int res=0;
while(bfs()){
memcpy(cur,head,sizeof(head));
res+=dfs(s,inf);
}
return res;
}
int main(){
n=read(),m=read();
int tot=0;
// printf("%d %d\n",cnt,top);
for(register int i=1;i<=n;++i){
a[i]=read();
if(!id[a[i]]) id[a[i]]=++cnt;
}
for(register int i=1;i<=n;++i) idc[i]=++cnt;
// printf("%d %d\n",cnt,top);
for(register int i=1;i<=n;++i){
for(register int j=1;j<=n-i+1;++j){
wd[i][i+j-1]=read();d[i][i+j-1]=++cnt;
}
}
s=++cnt;
t=++cnt;
// printf("%d %d\n",cnt,top);
for(register int len=n;len>=1;--len){
for(register int l=1;l<=n-len+1;++l){
int r=l+len-1;
if(l!=r){
add(d[l][r],d[l+1][r],inf);
add(d[l][r],d[l][r-1],inf);
}else{
add(d[l][r],idc[l],inf);
add(idc[l],t,a[l]);
add(d[l][r],id[a[l]],inf);
}
if(wd[l][r]>0) add(s,d[l][r],wd[l][r]),tot+=wd[l][r];
else if(wd[l][r]<0) add(d[l][r],t,-wd[l][r]);
}
}
// printf("%d %d\n",cnt,top);
for(register int i=1;i<=n;++i){
if(!aed[a[i]]){
add(id[a[i]],t,m*a[i]*a[i]);
aed[a[i]]=1;
}
}
// printf("%d %d\n",cnt,top);
/* for(int i=1;i<=cnt;i++){
for(int j=head[i];j;j=edge[j].nex){
int v=edge[j].v;
if(edge[j].w){
printf("%d %d %d\n",i,v,edge[j].w);
}
}
}*/
// printf("%d %d ed\n",cnt,top);
printf("%d",tot-dinic());
return 0;
} 星际战争
二分+dinic,这里使用dinic来判断是否可行,不能往费用流上面想
#include
#include
#include
#include
const double eps = 1e-4;
#define ll unsigned long long
using namespace std;
const int N=201,M=10001;
struct node{
int v,next;ll w;
}edge[M*2];
int top=1,head[N],cur[N];
const ll inf=1009092608170000ll;
inline void add(int from,int to,ll w){
edge[++top].v=to;edge[top].next=head[from];head[from]=top;edge[top].w=w;
edge[++top].v=from;edge[top].next=head[to];head[to]=top;edge[top].w=0;
}
inline int read(){
char ch=getchar();int x=0;int pos=1;
for(;!isdigit(ch);ch=getchar()) if(ch=='-') pos=0;
for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0';
return pos?x:-x;
}
int n,m,s,t;
int dir=0,level[N];
queueq;
inline ll Min(ll a,ll b){
return a>b?b:a;
}
inline int bfs(){
memset(level,-1,sizeof(level));
level[s]=0;q.push(s);
while(!q.empty()){
int now=q.front();q.pop();
for(int i=head[now];i;i=edge[i].next){
int v=edge[i].v;
if(level[v]==-1&&edge[i].w){
level[v]=level[now]+1;
q.push(v);
}
}
}
if(level[t]==-1) return 0;
else return 1;
}
inline ll dfs(int now,ll flow){
if(now==t) return flow;
ll res=flow;
for(int &i=cur[now];i;i=edge[i].next){
int v=edge[i].v;
if(edge[i].w&&level[v]==level[now]+1){
ll k=dfs(v,Min(edge[i].w,res));
res-=k;edge[i].w-=k;edge[i^1].w+=k;
}
if(!res) break;
}
return flow-res;
}
inline ll dinic(){
ll ans=0;
while(bfs()){
memcpy(cur,head,sizeof(head));
ans+=dfs(s,inf);
}
return ans;
}
ll a[N],b[N],tot;
int mp[N][N];
int check(double now){
s=n+m+1,t=n+m+2;
memset(head,0,sizeof(head));
for(int i=1;i<=top;i++){
edge[i].v=edge[i].next=edge[i].w=0;
}
top=1;
for(int i=1;i<=n;i++){
add(i+m,t,a[i]);
}
for(int i=1;i<=m;i++){
add(s,i,(ll)(now*b[i]));
for(int j=1;j<=n;j++){
if(mp[i][j]) add(i,j+m,inf);
}
}
if(dinic()==tot){
return 1;
}else return 0;
}
int main(){
n=read();m=read();
for(int i=1;i<=n;i++){
a[i]=read();a[i]*=1000ll;tot+=a[i];
}
for(int i=1;i<=m;i++){
b[i]=read();b[i]*=1000ll;
}
double l=0,r=0;
/*for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
}
}*/
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
mp[i][j]=read();
if(mp[i][j]) r+=(double)(a[j]/b[i]);
}
}
while(l 跟题解的扩大方式有丶不同
poj1149
建图方式的改变:如果考虑猪在猪圈流动,点数是O(nm)的,考虑在人之间流动点数是O(n)的
#include
#include
#include
#include
#include
using namespace std;
int read(){
int x=0,pos=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar()) if(ch=='-') pos=0;
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+ch-'0';
return pos?x:-x;
}
const int N = 1005,M=2000001;
const int inf = 192608170;
int n,m,s,t;
int head[N],cur[N],top=1;
struct node{
int v,nex,w;
}edge[M*2];
inline void add(int u,int v,int w){
edge[++top].v=v;edge[top].nex=head[u];edge[top].w=w;head[u]=top;
edge[++top].v=u;edge[top].nex=head[v];edge[top].w=0;head[v]=top;
}
int vis[N];
inline int bfs(){
memset(vis,-1,sizeof(vis));
queueq;
q.push(s);vis[s]=0;
while(!q.empty()){
int now=q.front();q.pop();
for(register int i=head[now];i;i=edge[i].nex){
int v=edge[i].v;
if(vis[v]==-1&&edge[i].w){
vis[v]=vis[now]+1;
q.push(v);
}
}
}
return vis[t]!=-1;
}
inline int dfs(int now,int flow){
int res=flow;
if(now==t||!flow) return flow;
for(int &i=cur[now];i;i=edge[i].nex){
int v=edge[i].v;
if(vis[v]==vis[now]+1&&edge[i].w){
int nw=dfs(v,min(res,edge[i].w));
edge[i].w-=nw;edge[i^1].w+=nw;res-=nw;
if(!res) break;
}
}
return flow-res;
}
inline int dinic(){
int res=0;
while(bfs()){
memcpy(cur,head,sizeof(head));
res+=dfs(s,inf);
}
return res;
}
int cont[N*12],las[N*12];
int main(){
m=read(),n=read();
s=n+1,t=n+2;
for(int i=1;i<=m;i++){
cont[i]=read();
}
for(int i=1;i<=n;i++){
int A=read();
for(int j=1;j<=A;j++){
int k=read();
if(!las[k]){
add(s,i,cont[k]);
las[k]=i;
}else{
add(las[k],i,inf);
las[k]=i;
}
}
int B=read();
add(i,t,B);
}
printf("%d",dinic());
return 0;
} CQOI2009 跳舞
限制模型,与一些点有限制,一些点没有限制可以拆点,拆出来的点中间连的边容量即为限制边数量上界
#include
#include
#include
#include
#include
using namespace std;
int read(){
int x=0,pos=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar()) if(ch=='-') pos=0;
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+ch-'0';
return pos?x:-x;
}
const int N = 305,M=2000001;
const int inf = 192608170;
int n,m,s,t,k,mp[N][N];
int head[N],cur[N],top=1;
struct node{
int v,nex,w;
}edge[M*2];
inline void add(int u,int v,int w){
edge[++top].v=v;edge[top].nex=head[u];edge[top].w=w;head[u]=top;
edge[++top].v=u;edge[top].nex=head[v];edge[top].w=0;head[v]=top;
}
int vis[N];
inline int bfs(){
memset(vis,-1,sizeof(vis));
queueq;
q.push(s);vis[s]=0;
while(!q.empty()){
int now=q.front();q.pop();
for(register int i=head[now];i;i=edge[i].nex){
int v=edge[i].v;
if(vis[v]==-1&&edge[i].w){
vis[v]=vis[now]+1;
q.push(v);
}
}
}
return vis[t]!=-1;
}
inline int dfs(int now,int flow){
int res=flow;
if(now==t||!flow) return flow;
for(int &i=cur[now];i;i=edge[i].nex){
int v=edge[i].v;
if(vis[v]==vis[now]+1&&edge[i].w){
int nw=dfs(v,min(res,edge[i].w));
edge[i].w-=nw;edge[i^1].w+=nw;res-=nw;
if(!res) break;
}
}
return flow-res;
}
inline int dinic(){
int res=0;
while(bfs()){
memcpy(cur,head,sizeof(head));
res+=dfs(s,inf);
}
return res;
}
int check(int mid){
memset(head,0,sizeof head);
for(int i=1;i<=top;i++){
edge[i].v=edge[i].nex=edge[i].w=0;
}
top=1;
for(int i=1;i<=n;i++){
add(s,i,mid);
add(i+n*3,t,mid);
add(i,i+n,k);
add(i+n*2,i+n*3,k);
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(mp[i][j]){
add(i,j+n*3,1);
}else{
add(i+n,j+n*2,1);
}
}
}
if(dinic()==mid*n){
return 1;
}else return 0;
}
char S[N];
int main(){
n=read(),k=read();s=n*4+1,t=n*4+2;
for(int i=1;i<=n;i++){
scanf("%s",S);
for(int j=1;j<=n;j++){
mp[i][j]=S[j-1]=='Y';
}
}
int l=0,r=n+1;
while(l>1;
if(check(mid)) l=mid;
else r=mid;
}
printf("%d",l);
return 0;
}