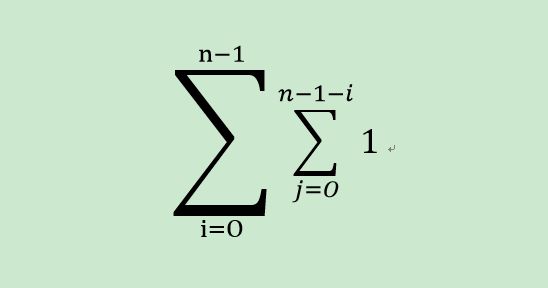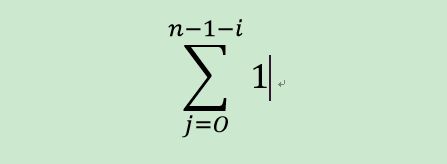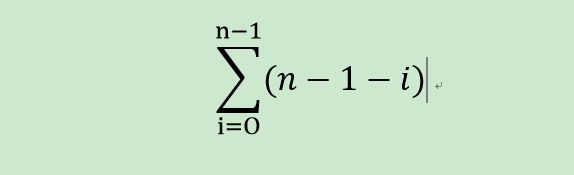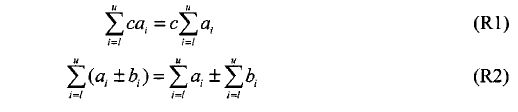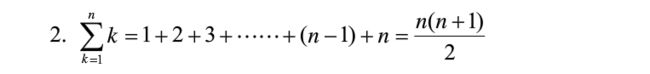本文内容:
1、什么是冒泡排序?
2、冒泡排序的 C/OC 实现与算法分析。
算法总目录:算法?
1、什么是冒泡排序?
冒泡排序:每次比较两个相邻的元素,如果它们的顺序错误就把它们交换过来。
核心点 :相邻元素、比较、交换
冒泡排序的过程【请放大图片,从下往上,从左往右,看】:伪代码:
/*
功能:用冒泡排序对数组 A[0 .. n - 1] 进行排序
输入:一个可排序的数组 A[0 .. n - 1],即能够对数据进行比较操作
输出:升序排列的数组,即左小右大
注:也可以用链表来代替数组;
*/
BoubbleSort( A[0 .. n - 1] )
for i <-- 0 to n - 2 do
for j <-- 0 to n - 2 - i do
if A[j + 1] < A[j] swap A[j] and A[j + 1]
2、冒泡排序的 C/OC 实现与算法分析。
- C 实现:
typedef enum _CompareResult {
LESS = -1,
SAME = 0,
GRATER = 1,
} CompareResult;
typedef enum {
FALSE = 0,
TRUE = 1,
}BOOL;
typedef unsigned int uint;
typedef BOOL(*Compare)(void * array, uint idx1, uint idx2);
typedef void(*Swap)(void * array, uint idx1, uint idx2);
typedef size_t ArrayCount;
/*
功能:利用冒泡排序原理,对数据进行重新排序
参数 array : 要排序的数组
参数 count : 数组的长度
参数 compare : 数据的具体比较函数
参数 swap : 数据的具体交换函数
*/
void BubbleSort(void * array, ArrayCount count, Compare compare, Swap swap) {
if (array == NULL || compare == NULL || swap == NULL) { return; }
for (unsigned int i = 0; i < (count - 1); i++) {
for (unsigned int j = 0; j < (count - 1 - i); j++) {
if (compare(array, j + 1, j)) {
swap(array, j, j + 1);
}
}
}
}
// MARK: 低配版 [ 升序 ]
void BubbleSort(int *array, unsigned int count) {
if (array == NULL || count <= 0) { return; }
int temp = 0;
for (unsigned int i = 0; i < (count - 1); i++) {
for (unsigned int j = 0; j < (count - 1 - i); j++) {
if (array[j + 1] < array[j]) {
temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
}
}
}
}
Main 中的测试代码:
// 声明
void BubbleSort(void * array, ArrayCount count, Compare compare, Swap swap);
BOOL CompareData(void * array, uint idx1, uint idx2);
void SwapData(void * array, uint idx1, uint idx2);
typedef float ElementType;
#define ARRAY_COUNT 5
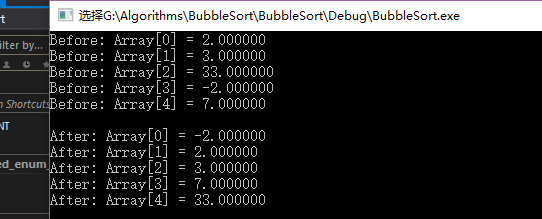
int main() {
ElementType array[ARRAY_COUNT] = {2, 3, 33, -2, 7};
uint idx = 0;
do {
printf("Before: Array[%d] = %f\n", idx, array[idx]);
idx++;
} while (idx < ARRAY_COUNT);
BubbleSort(array, ARRAY_COUNT, CompareData, SwapData);
printf("\n");
idx = 0;
do {
printf("After: Array[%d] = %f\n", idx, array[idx]);
idx++;
} while (idx < ARRAY_COUNT);
// Pause
getchar(); getchar();
return 0;
}
// MARK: Compare & Swap
#if 0
#define Reverse
#endif
BOOL CompareData(void * array, uint idx1, uint idx2) {
ElementType *arr = (ElementType *)array;
#ifdef Reverse
return ( (arr[idx1] > arr[idx2]) ? TRUE : FALSE );
#else
return ((arr[idx1] < arr[idx2]) ? TRUE : FALSE);
#endif
}
void SwapData(void * array, uint idx1, uint idx2) {
ElementType *arr = (ElementType *)array;
ElementType temp = arr[idx1];
arr[idx1] = arr[idx2];
arr[idx2] = temp;
}
算法分析:
void BubbleSort(void * array, ArrayCount count, Compare compare, Swap swap) {
if (array == NULL || compare == NULL || swap == NULL) { return; }
for (unsigned int i = 0; i < (count - 1); i++) {
for (unsigned int j = 0; j < (count - 1 - i); j++) {
if (compare(array, j + 1, j)) {
swap(array, j, j + 1);
}
}
}
}
解析:从实现代码就可以直接看出来它不是递归的实现方式;
1、输入规模:count 【就是 n】
2、算法基本操作:
if (compare(array, j + 1, j)) 【先有比较再有交换】
3、是否只依赖输入规模:
compare(array, j + 1, j) 形参是
array 数组元素、
j + 1 和
j 都是属于 [0 ~ (count - i - 1)],而其中的 i 属于 [0 ~ (count - 1)],由此可知,compare 只依赖于输入规模这个条件;所以不用考虑最差、最优、平均效率;
【观察基本操作本身,以及基本操作的上层操作,如:那两个 for 循环】
4、建立表达式并求出增长次数:
从外向里看,第一个 for 循环,简化表示有,
for (unsigned int i = 0; i < (count - 1); i++) {
Opreatipons();
}
那么 Opreatipons(); 被执行的次数就是:(n - 1),当且仅当,数组有序且第一个和第二个元素只要交换一次数组就完成排序时,冒泡排序的时间复杂度为:Θ (n) ;
展开 Operations 有:
for (unsigned int i = 0; i < (count - 1); i++) {
for (unsigned int j = 0; j < (count - 1 - i); j++) {
Ops();
}
}
慢慢来:
当 i = 0 时,j 从 0 到 ( count - 1 - 0 ) --> ( count - 1 ) ;
当 i = 1 时,j 从 0 到 ( count - 1 - 1 ) --> ( count - 2 ) ;
...
当 i = count - 2 时,j 从 0 到 ( count - 1 - ( count - 2 ) ) --> 1;
当 i = count - 1 时,j 从 0 到 ( count - 1 - ( count - 1 ) ) --> 0;
即两个循环结束后, j 的值就是从 0 一直加到 count - 1 ;就是一个等差数列:
代入公式有[ d = 1 ]:
C(n) = (count - 1) * 0 + 0.5 * ((count - 1) * (count - 1 - 1)) * 1 ;
C(n) = 0.5 * (count 2 - 3 * count + 2);
则可有冒泡排序的时间复杂度为:Θ (n 2) 还有第二种分析方式:
同理的:
从外向里看,第一个 for 循环,简化表示有,
for (unsigned int i = 0; i < (count - 1); i++) {
Opreatipons();
}
展开 Operations 有:
for (unsigned int i = 0; i < (count - 1); i++) {
for (unsigned int j = 0; j < (count - 1 - i); j++) {
Ops();
}
}
又因为 Ops() 里面我们只关心核心基本操作 if (compare(array, j + 1, j)),而这个比较的次数是一次;
现在就简化它:
4、最终简化为:
则有冒泡排序的时间复杂度为:Θ (n 2)
- Objective-C (OC) 实现:
【OC 这里因为看不到源代码,所以是不是冒泡算法,就很难说,但它符合错误就交换这种思想】
// OC 中的 NSComparisonResult 定义:
/* typedef NS_ENUM(NSInteger, NSComparisonResult) {
NSOrderedAscending = -1L,
NSOrderedSame,
NSOrderedDescending
};*/
typedef NSComparisonResult (*CompareObject)(id obj1, id obj2);
/*
功能:利用冒泡排序对数组进行重新排序
参数 array:需要重新排序的数组
参数 compare:数组元素的比较方法
返回值:已经排好序的数组
*/
NSArray * BubbleSort(NSArray *array, CompareObject compare) {
if (compare == NULL) { return array; }
NSArray *sorted = [array sortedArrayUsingComparator:^NSComparisonResult(id _Nonnull obj1, id _Nonnull obj2) {
return compare(obj1, obj2);
}];
return sorted;
}
// MARK: 低配版(升序)
NSArray * BubbleSort(NSArray *array, CompareObject compare) {
if (compare == NULL) { return array; }
NSMutableArray *sorted = [array mutableCopy];
NSUInteger count = sorted.count;
for (NSUInteger i = 0; i < ( count - 1); i++) {
for (NSUInteger j = 0; j < ( count - 1 - i ); j++) {
id obj1 = [sorted objectAtIndex:j];
id obj2 = [sorted objectAtIndex:(j + 1)];
if (compare(obj1, obj2) == NSOrderedAscending ) {
[sorted exchangeObjectAtIndex:j withObjectAtIndex:(j + 1)];
}
}
}
return sorted.copy;
}
Main 中的测试代码:
NSArray * BubbleSort(NSArray *array, CompareObject compare);
NSComparisonResult CompareData(id obj1, id obj2);
// MARK: Main
int main(int argc, const char * argv[]) {
@autoreleasepool {
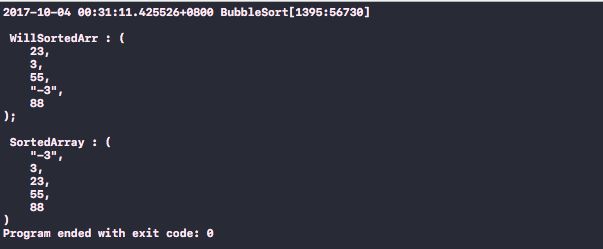
NSArray *willSortedArr = @[@(23), @(3), @(55), @(-3), @(88)];
NSArray *sortedArr = BubbleSort(willSortedArr, CompareData);
NSLog(@"\n\r WillSortedArr : %@; \n\r SortedArray : %@", willSortedArr, sortedArr);
}
return 0;
}
// MARK: Compare Function
// 默认是升序,开启 Reverse 就直接变成降序
#if 1
#define Reverse
#endif
NSComparisonResult CompareData(id obj1, id obj2) {
NSNumber *n1 = (NSNumber *)obj1;
NSNumber *n2 = (NSNumber *)obj2;
#ifdef Reverse
if ([n1 integerValue] < [n2 integerValue]) { return NSOrderedAscending; }
return NSOrderedDescending;
#else
if ([n1 integerValue] < [n2 integerValue]) { return NSOrderedDescending; }
return NSOrderedAscending;
#endif
}
参考书籍/文章:
书籍:《算法设计与分析基础 美 莱维汀 第3版》
书籍:《啊哈!算法》
文章:常用的累加∑公式
如有错漏,还望指出,不胜感激!
我的博客即将搬运同步至腾讯云+社区,邀请大家一同入驻:https://cloud.tencent.com/developer/support-plan?invite_code=2zleyndcg90k8