大纲
1、数据库基本原理
2、关系代数
一、数据库基本原理
早期文件系统的缺陷:
(1)数据冗余(Redundancy)。由于文件之间缺乏联系,同样的文件可能会多次存储。
(2)不一致性(Inconsistency)。数据冗余,在进行更新操作时造成的后果。
(3)数据孤立,数据联系弱(Poor Data Relationship)。
完整性问题,原子性问题,并发访问异常,安全性问题。
学习方法:类比自己已经熟知或者学会的知识点,通过对比学习。为什么需要它?有什么优势? 解决了什么问题?
文件系统管理的缺陷:
数据冗余和不一致性
数据访问困难(在大文件中查找特定的行,或者在多个文件中查找有关系的行)
数据孤立,数据之间联系弱
完整性问题
原子性问题
并发访问异常
安全性问题(授权,访问权限)
因为有上述的问题,所以, 数据库管理系统就是为了解决上面的问题。 怎么解决的?
文件系统:
表示层: 文件(对于我们用户来说,表现为一个文件)
逻辑层:文件系统,存储引擎(实现表示层和物理层之间的映射)
物理层:元数据 inode , 数据 datablock
关系型数据库:(基于文件系统的再一次抽象)
表示层:二维表
逻辑层:存储引擎
物理层:数据文件(文件系统层面)
约束:
域约束:数据类型约束
检查性约束:取值范围
外键约束:引用完整性约束
主键约束:某字段能唯一标识表中的实体,并且不允许为空
一张表中只能有一个主键
唯一性约束:每一行的某字段都不允许出现相同值,可以为空
一张表中可以有多个唯一性约束
上述文件系统的缺陷,催生了 数据库管理软件的产生。
数据管理进入数据库阶段的标志是:IMS系统(层次型数据库),DBTG报告(网状数据库) 和 E.F.Code(关系型数据) 的文章。
1970年E.F.Code发表“A Relational Model of Data for Large Shared Data Banks”一文,奠定了关系型数据库的理论基础,建立在集合论和谓词演算的基础上。关系模型数据库系统的数据结构简单,表示数据及其数据之间的联系均采用关系(二维表,二维关系),同时关系模型有扎实的数学理论做基础,使得数据的操作可以通过关系的运算(集合论和谓词演算)来完成。
采用数据库模型表示复杂的数据结构。数据模型不仅描述数据本身的特征,还要描述数据之间的联系。
数据库设计的全过程,可以分成3个阶段:第一个阶段为数据库需求分析;第二个阶段为建立概念数据模型;第三个阶段为逻辑设计以及物理实现阶段。
数据描述也就是上述二、三两个阶段细化:
阶段一:
概念设计中的数据描述: 实体(Entity), 实体集(Entity Set), 属性(Attribute), 实体标识符(Identifier):能唯一标识实体的属性或属性集。
阶段二:
逻辑设计中的数据描述:字段(Field),记录(Record),文件(File),键(Key)。
阶段三:
物理介质中的数据描述:二进制
数据联系(Relationship)
二元联系有以下三种类型:
一对一联系
一对多联系
多对多联系:多对多关系也很常见,例如学生与选修课之间的关系,一个学生可以选择多门选修课,而每个选修课又可以被多名学生选择。数据库中的多对多关联关系一般需采用中间表的方式处理,将多对多转化为两个一对多的形式。
数据模型
模型是对现实世界的抽象。能表示实体类型及实体间联系的模型称为“数据模型”(Data Model)。
概念模型:按用户的观点对数据建模,独立于计算机系统的数据模型,是对现实世界的第一层抽象。
逻辑模型:直接面向数据库的逻辑结构,它是对现实世界的第二层抽象。
实体关系(ER)模型的目标是捕获现实世界的数据需求,并以简单、易理解的方式表现出来。ER模型可用于项目组内部交流或用于与用户讨论系统数据需求。
为什么需要ER图? 建筑师总是和客户交谈,按其需要作出设计图,然后让客户确认再施工;同理,在软件开发过程中,我们在具体建立数据库之前,也应该按照客户需求,画出ER图以让其确认,然后再创建数据库和表。ER图就是“建筑设计篮图”。
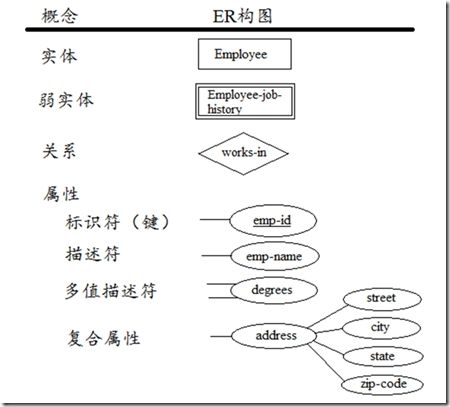
ER模型中的基本元素
基本的ER模型包含三类元素:实体、关系、属性
实体(Entities):实体是首要的数据对象,常用于表示一个人、地方、某样事物或某个事件。一个特定的实体被称为实体实例(entity instance或entity occurrence)。实体用长方形框表示,实体的名称标识在框内。一般名称单词的首字母大写。
关系(Relationships):关系表示一个或多个实体之间的联系。关系依赖于实体,一般没有物理概念上的存在。关系最常用来表示实体之间,一对一,一对多,多对多的对应。关系的构图是一个菱形,关系的名称一般为动词。关系的端点联系着角色(role)。一般情况下角色名可以省略,因为实体名和关系名已经能清楚的反应角色的概念,但有些情况下我们需标出角色名来避免歧义。
属性(Attributes):属性为实体提供详细的描述信息。一个特定实体的某个属性被称为属性值。Employee实体的属性可能有:emp-id, emp-name, emp-address, phone-no……。属性一般以椭圆形表示,并与描述的实体连接。属性可被分为两类:标识符(identifiers),描述符(descriptors)。Identifiers可以唯一标识实体的一个实例(key),可以由多个属性组成。ER图中通过在属性名下加上下划线来标识。多值属性(multivalued attributes)用两条线与实体连接,eg:hobbies属性(一个人可能有多个hobby,如reading,movies…)。复合属性(Complex attributes)本身还有其它属性。
辨别强实体与弱实体:强实体内部有唯一的标识符。弱实体(weak entities)的标识符来自于一个或多个其它强实体。弱实体用双线长方形框表示,依赖于强实体而存在。
画ER图指导
确定系统中的实体(用矩形表示)
确定每个实体的属性(用椭圆表示)
确定实体间的关系(用菱形表示)
关系模型
关系模型(Relational Model)的主要特征是用二维表格表达实体集,记录之间的联系通过模式的键体现。
关系模型的完整性规则:
实体完整性(唯一性):关系中元组的主键值不能为空
参照完整性规则(一致性):外键必须是另一个表的主键的 有效取值,或者是一个空值
用户定义完整性规则(正确、有效性):客观事实,比如年龄不能小于零。
“关系”(relation)是数学中的一个基本概念,由集合中的任意元素所组成的若干有序偶对表示,用以反应客观事物间的一定关系。被定义为一个笛卡尔积的子集。
关系规则
规则1:第一范式规则。在定义的表中,关系模型坚持不允许含有多值属性和含有内部结构的列。
规则2:只能给予内容存取行规则。只能通过行的内容即每一行中所存在的属性值来检索列。你无法建立一个指向行的指针以便以后可以再次检索它。但是可以被打破,通过行标识(row identification, RID)提供永和检索表中的行的方法。
规则3:行唯一性规则。关系中的任何两个元祖的值在同一时刻不能是完全相同的。
规则4:实体完整性规则。表中的任意行在主键列的取值都不允许为NULL
关系的键
一个关系总是有一个唯一的标识符,它是一个字段或者是一组字段(属性),其值在关系的元祖中自始自终是唯一的,每个元祖都是不同的并且可以有一个或多个称为键的属性标识,键总是提供唯一性质的最小的属性序列。
超键(表中的任意两行数据在该列集合上都是唯一的)
超键是一个属性或属性集合,它唯一的标识了一个关系中的元祖,关系中所有的属性组合在一起也是一个超键,因为关系中只有一行又给定的额全部关系属性的值。
候选键(组成键的列的集合中在也没有子集也是表的超键)
当有多个属性或属性组可以作为唯一标识符时,他们就被称为候选键,也可以将候选键看成没有冗余的超键。
数学定义:给定一个表T,属性集为A1.A2…An,表T的候选键,是具有以下两个特征的一组属性的集合K=An1 , An2 ,…Anm
(1) 如果u,v是T中的两个不同元祖,集合K中必定存在至少一个列Anm,使得u[Anm] != v[Anm]
(2) 没有K的真子集H具有特征1
主键
主键是一个候选键,它是从关系中挑选出来用于唯一标识元组的。
在实际应用中,通常额外添加一列作为主键,而不建议用数据的某个列来作为主键。
外键
外键可以定义为一个属性或多个属性的集合,它在一个关系中匹配一些其他关系中的候选键。表之间存在”关系“,当一个表中的主键在另一个表中也作为一个属性存在时,就叫做外键。通俗的说外键的意思就是【来自、引用、参考】(一个表列的数据完全来自另一个表的某个列值)。
举例:公司每名员工(Employee)都应该归属于一个部门(Department),那么员工和部门之间便有了一定的关系,我们由此来确定外键。
主键:cEmployeeCode 外键:cDepartmentCode
主键:cDepartmentCode
数据库设计三大范式
为了建立冗余较小、结构合理的数据库,设计数据库时必须遵循一定的规则。在关系型数据库中这种规则就称为范式。范式是符合某一种设计要求的总结。要想设计一个结构合理的关系型数据库,必须满足一定的范式。
1.第一范式(确保每列保持原子性)
第一范式是最基本的范式。如果数据库表中的所有字段值都是不可分解的原子值,就说明该数据库表满足了第一范式。1NF 很好辨别,但是 2NF 和 3NF 就容易搞混淆。
第一范式的合理遵循需要根据系统的实际需求来定。比如某些数据库系统中需要用到“地址”这个属性,本来直接将“地址”属性设计成一个数据库表的字段就行。但是如果系统经常会访问“地址”属性中的“城市”部分,那么就非要将“地址”这个属性重新拆分为省份、城市、详细地址等多个部分进行存储,这样在对地址中某一部分操作的时候将非常方便。这样设计才算满足了数据库的第一范式,如下表所示。
上表所示的用户信息遵循了第一范式的要求,这样在对用户使用城市进行分类的时候就非常方便,也提高了数据库的性能。
2.第二范式(确保表中的每列都和主键相关)
第二范式在第一范式的基础之上更进一层,首先满足1NF。第二范式需要确保数据库表中必须有主键, 而是表中的每一列都和主键相关,而不能只与主键的某一部分相关(主要针对联合主键而言)。也就是说在一个数据库表中,一个表中只能保存一种数据,不可以把多种数据保存在同一张数据库表中。
比如要设计一个订单信息表,因为订单中可能会有多种商品,所以要将订单编号和商品编号作为数据库表的联合主键,如下表所示。
订单信息表
这样就产生一个问题:这个表中是以订单编号和商品编号作为联合主键。这样在该表中商品名称、单位、商品价格等信息不与该表的主键相关,而仅仅是与商品编号相关。所以在这里违反了第二范式的设计原则。
而如果把这个订单信息表进行拆分,把商品信息分离到另一个表中,把订单项目表也分离到另一个表中,就非常完美了。如下所示。
这样设计,在很大程度上减小了数据库的冗余。如果要获取订单的商品信息,使用商品编号到商品信息表中查询即可。
3.第三范式(确保每列都和主键列直接相关,而不是间接相关)
第三范式又在第二范式基础上在进一层,必须满足2NF。 第三范式需要确保数据表中的每一列数据都和主键直接相关,而不能间接相关。非主键列必须直接依赖于主键,不能存在传递依赖。即不能存在:非主键列 A 依赖于非主键列 B,非主键列 B 依赖于主键的情况。
比如在设计一个订单数据表的时候,可以将客户编号作为一个外键和订单表建立相应的关系。而不可以在订单表中添加关于客户其它信息(比如姓名、所属公司等)的字段。如下面这两个表所示的设计就是一个满足第三范式的数据库表。
这样在查询订单信息的时候,就可以使用客户编号来引用客户信息表中的记录,也不必在订单信息表中多次输入客户信息的内容,减小了数据冗余。
二、关系代数
关系运算理论是关系数据库查询语言的理论基础。
关系代数:以集合操作为基础
关系演算:以谓词验算为基础
笛卡尔积 ,从数学角度理解,就是将集合A和集合B中所有有序对元素集合。
例如:假设集合A={a,b},集合B={0,1,2},则两个集合的笛卡尔积为{(a,0),(a,1),(a,2),(b,0),(b,1), (b,2)}。即若R有k1个元组,S有k2个元组,则关系R和S的笛卡尔积有k1 * k2个元组。
全码:关系模式中所有属性组都是这个关系模式的候选码。
SELECT * FROM table1 CROSS JOIN table2
没有 WHERE 子句的交叉联接将产生联接所涉及的表的笛卡尔积。第一个表的行数乘以第二个表的行数等于笛卡尔积结果集的大小。
不过,如果添加一个 WHERE 子句,则交叉联接的作用将同内联接一样。
注意:不能使用ON 关键字,只能用WHERE条件
并(Union)
设关系A和关系B具有相同的元数n(即两个关系都有n个属性),且相应的属性取自同一个域,则关系A和关系B的并由属于A或属于B的元组组成。
使用 UNION 运算符组合多个结果
SELECT name,num FROM Table1 UNION SELECT name,num FROM Table2
注意:查询的字段个数必须相同,Table2的字段类型要跟Table1的相同.
如果使用 UNION 运算符,那么单独的 SELECT 语句不能包含其自己的 ORDER BY 或 COMPUTE 子句。只能在最后一个 SELECT 语句的后面使用一个 ORDER BY 或 COMPUTE 子句;该子句适用于最终的组合结果集。GROUP BY 和 HAVING 子句只能在单独的 SELECT 语句中指定。
只用UNION有重复记录只取一条,用UNION ALL 时取所有重复记录
差(Difference)
设关系A和关系B具有相同的元数n(即两个关系都有n个属性),且相应的属性取自同一个域,则关系B和关系A的差由属于B而不属于A的元组组成。
NOT IN 表示差集
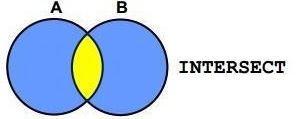
交(Intersection)
设关系A和关系B具有相同的元数n(即两个关系都有n个属性),且相应的属性取自同一个域,则关系A和关系B的交由属于A并且又属于B的元组组成。
投影(Projection)
投影操作是对一个给定的关系去掉若干属性,对一个k元组的关系R来说,如果我们想留下第i1,i2,i3 … im,(m<=k)个属性,则我们可以把不在这些属性列表里的属性(字段)去掉。投影运算可以表示为πi1,i2,i3 … im(R)。
选择(Selection)
连接(Join)
从两个关系的笛卡尔积中选取属性间满足一定条件的元组。其中A和B分别为R和S上度数相等且可比的属性组。θ是比较运算符。连接运算从R和S的笛卡尔积R×S中选取(R关系)在A属性组上的值与(S关系)在B属性组上值满足比较关系θ的元组。
理解:从笛卡尔积中选择满足一定条件的部分行。join 就是笛卡尔积和选择操作的组合。
除法(Division)
除法是写为R ÷ S 的二元关系。其结果由R中元组到唯一于R的属性名字(就是说只在R表头中而不在S表头中的属性)的限制构成,并且它们与S中的元组的所有组合都存在于R中。
更形式的说除法的语义定义如下:
R÷ S= { t[a1,...,an] : t RsS( (t[a1,...,an]s)R) }
这里的{a1,...,an}是唯一于R的属性名字的集合而t[a1,...,an]是t到这个集合的限制。通常要求在S的表头中的属性名字是R的表头的属性名字的子集,否则运算的结果永远为空。
除法可以用基本运算模拟如下。我们假定a1,...,an是唯一于R的属性名字而b1,...,bm是S的属性名字。在第一步中我们投影R于它的唯一属性上,并接着构造它们与S的元组的所有组合:
T:= πa1,...,an(R) × S
在上面例子中,T将是表示所有学生(因为Student是“完成”表的唯一键/属性)与所有给定任务的组合的表。所以Eugene在T中将有两行Eugene -> Database1 和Eugene -> Database2。
在下个步骤中,我们从这个关系中减去R:
U:= T- R
注意在U的都是R中没有出现的可能的组合。所以如果现在做到唯一于R的属性名字的投影,则我们有了R中元组的限制,它们与S的元组的所有组合未都出现在R中:
V:= πa1,...,an(U)
剩下的就是投影R到唯一于它的属性名字并减去V:
W:= πa1,...,an(R) - V
运算依赖
给定两个表R和S,R和S的连接可以用积、选择、投影等方式重写。
除法可以用投影、乘积、差等方式表达。