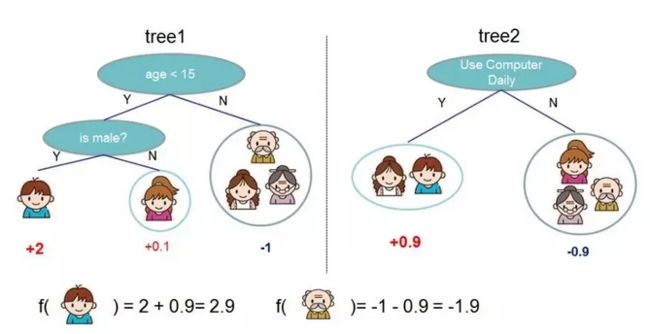
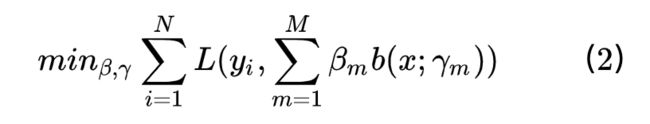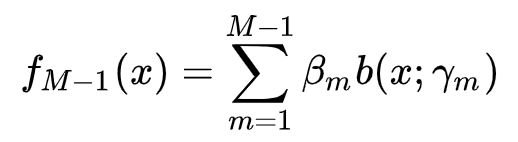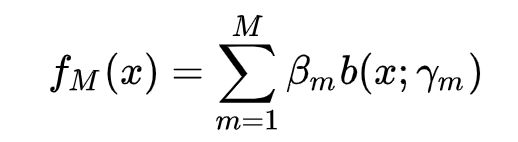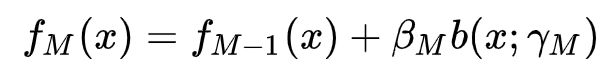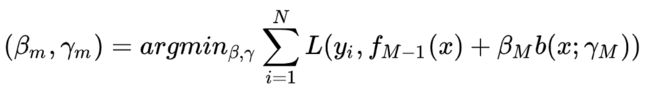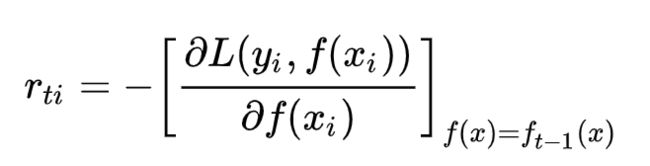GBDT:gradient boosting decision tree 梯度增强决策树
GBDT是一种采用加法模型（即基函数的线性组合）与前向分步算法并以决策树作为基函数的提升方法。通俗来说就是，该算法由多棵决策树组成，所有树的结论加起来形成最终答案。
GBDT全称Gradient Boosting Decison Tree，同为Boosting家族的一员，它和Adaboost有很大的不同。Adaboost 是利用前一轮弱学习器的误差率来更新训练集的权重，这样一轮轮的迭代下去，简单的说是Boosting框架+任意基学习器算法+指数损失函数。
GBDT也是迭代，也使用了前向分布算法，但是弱学习器限定了只能使用CART回归树模型，同时迭代思路和Adaboost也有所不同，简单的说Boosting框架+CART回归树模型+任意损失函数。
GBDT作为boosting算法中的另一个重要代表。主要由三部分构成
①GB，Gradient Boosting（梯度迭代）
②DT，Regression Decision Tree（回归树），GBDT中的决策树与C4.5之类的分类决策树不同，属于CART回归树。虽然GBDT可以通过调整用于分类，但是其本质上还是属于回归树。
③Shrinkage ，Shrinkage（缩减）的思想认为，每次走一小步逐渐逼近结果的效果，要比每次迈一大步很快逼近结果的方式更容易避免过拟合。
GBDT思想
GBDT是集成学习Boosting家族的成员。弱学习器限定了只能使用CART回归树模型，迭代是思路是：在本轮迭代中找到一个CART回归树模型的弱学习器使得本轮的损失函数最小。即拟合误差。（Adaboost是利用前一轮迭代弱学习器的误差率来更新训练集的权重，这样一轮轮的迭代下去。）
GBDT的思想使其具有天然优势可以发现多种有区分性的特征以及特征组合。
回归树（Regression Decision Tree）
回归树生成算法：（CART）
提升树（Boosting Decision Tree）
提升方法采用加法模型和前向分布算法。以决策树为基函数的提升方法称为提升树。
提升树是迭代多棵回归树来共同决策。当采用平方误差损失函数时，每一棵回归树学习的是之前所有树的结论和残差，拟合得到一个当前的残差回归树，残差的意义如公式：残差 = 真实值 - 预测值 。提升树即是整个迭代过程生成的回归树的累加。
回归问题的提升树算法流程：
梯度提升决策树
对于一般的损失函数，往往每一步优化没那么容易，如绝对值损失函数和Huber损失函数。针对这一问题，Freidman提出了梯度提升算法：利用最速下降的近似方法，即利用损失函数的负梯度在当前模型的值，作为回归问题中提升树算法的残差的近似值，拟合一个回归树。
算法流程：
前向分布算法
- 1.1 加载模型 (基学习器的一种线性模型)其中， 为基函数，作为基函数的参数，作为基函数的系数。
在给定训练数据的损失函数的条件下，学习加法模型成为损失函数极小化问题：(同时求解那么多参数)
前向分步算法求解这一优化问题的思路：因为学习的是加法模型，如果能够从前向后，每一步只学习一个基函数及其系数，逐步去逼近上述的目标函数式，就可简化优化的复杂度，每一步只需优化如下损失函数： (每步学习一个基函数和系数)
前向分步算法流程：
输入：训练数据集T=；损失函数；基函数集；输出：加法模型
(1) 初始化
(2) 对 .
- 极小化损失函数得到参数
- 更新
(3)得到加法模型可见，前向分步算法将同时求解从m\u003d1到M所有参数 的优化问题简化成逐步求解各个 的优化问题了
2.负梯度拟合\n### 2.1.提升树算法\n\n了解完前向分步算法，再来看看什么是提升树算法。\n\n提升方法实际采用加法模型与前向分步算法，以决策树作为基函数的提升方法称为提升树。注意，这里的决策树为CART回归树，不是分类树。当问题是分类问题时，采用的决策树模型为分类回归树。为什么要采用决策树作为基函数呢？它有以下优缺点：\n\n优点\n\n可解释性强\n可处理混合类型特征\n具有伸缩不变性（不用归一化特征）\n有特征组合的作用\n可自然处理缺失值\n对异常点鲁棒\n有特征选择作用\n可扩展性强，容易并行\n缺点\n\n缺乏平滑性（回归预测时输出值只能是输出有限的若干种数值）\n不适合处理高维稀疏数据\n由于树的线性组合可以很好地拟合训练数据，即使数据中的输入与输出之间的关系很复杂也是如此。\n\n提升树模型可表示为：\n\n\n\n其中， 表示决策树; 为决策树的参数;M为树的个数;M为树的个数。\n\n针对不同的问题，提升树算法的形式有所不同，其主要区别在于使用的损失函数不同。而损失函数的不同，决策树要拟合的值也会不同。就一般而言，对于回归问题的提升树算法来说，若损失函数是平方损失函数，每一步只需简单拟合当前模型的残差。\n\n下面看一下在回归问题下，损失函数为平方损失函数的算法流程：输入：训练数据集T\u003d ；\n\n输出：提升树 \n\n(1)初始化 \n\n(2)对m\u003d1,2,...,M\n\n(a)计算残差\n\n\n\n(b)拟合残差 学习一个回归树，得到 \n\n(c)更新\n\n(3)得到回归问题提升树\n\n
前向分步算法流程：
输入：训练数据集T=[图片上传失败...(image-f0a7da-1565400358596)]
；损失函数[图片上传失败...(image-2ee4eb-1565400358596)]
；基函数集[图片上传失败...(image-c6c2f3-1565400358596)]
；
输出：加法模型f(x)
(1) 初始化 [图片上传失败...(image-4e9250-1565400358596)]
(2) 对m=1,2,...,M
(a) 极小化损失函数
[图片上传失败...(image-463054-1565400358596)]
得到参数 [图片上传失败...(image-725c23-1565400358596)]
(b)更新
[图片上传失败...(image-74f0bd-1565400358596)]
(3)得到加法模型
[图片上传失败...(image-c29770-1565400358596)]
可见，前向分步算法将同时求解从m=1到M所有参数 [图片上传失败...(image-6c0b7f-1565400358596)]
的优化问题简化成逐步求解各个 [图片上传失败...(image-a70f0f-1565400358596)]
的优化问题了
负梯度拟合
针对各种各样损失函数如何让进行通用性拟合的问题，Freidman提出了用损失函数的负梯度来拟合本轮损失的近似值，进而拟合一个CART回归树。
第t轮的第i个样本的损失函数的负梯度表示为：
拟合得到CART回归树后，针对每一个叶子节点里的样本，我们求出使损失函数最小，也就是拟合叶子节点最好的的输出值ctjctj如下：z
得到本轮的决策树拟合函数：
从而得到本轮的强学习器如下：
损失函数
指数损失函数
对数损失函数
-（二分类）
-（多分类）
回归算法
输入是训练集样本,最大迭代次数, 损失函数。输出是强学习器:
1.初始化弱学习器
2.对迭代轮数有：
(1)对样本计算负梯度
(2)利用拟合一颗CART回归树,得到第t颗回归树，其对应的叶子节点区域为其中J为回归树t的叶子节点的个数。
(3) 对叶子区域j =1,2,…J,计算最佳拟合值
(4) 更新强学习器
4.得到强学习器f(x)的表达式
二分类，多分类算法
GBDT的分类算法本质上和GBDT的回归算法没有区别，但是由于最后输出不是连续的值，而是离散的类别，导致我们无法直接从输出类别去拟合类别输出的误差。
目前主要有两个方法
1.指数损失函数，此时GBDT退化为Adaboost算法。
2.对数似然损失函数的方法。用类别的预测概率值和真实概率值的差来拟合损失。
●二元分类
二元分类的损失函数类似于逻辑回归对数似然损失函数：
其中
则此时的负梯度误差为:
对于生成的决策树，我们各个叶子节点的最佳残差拟合值为:
由于上式比较难优化，我们一般使用近似值代替:
除了负梯度计算和叶子节点的最佳残差拟合的线性搜索，二元GBDT分类和GBDT回归算法过程相同。
●多元分类
我们的对数似然损失函数为：
其中如果样本输出类别为k，则
第k类的概率的表达式为：
集合上两式，我们可以计算出第t tt轮的第i ii个样本对应l ll类别的负梯度误差为：
观察上式可以看出，其实这里的误差就是样本对应类别的真实概率和轮预测概率的差值。
由于上式比较难优化，我们一般使用近似值代替
对于生成的决策树，我们各个叶子节点的最佳残差拟合值为
除了负梯度计算和叶子节点的最佳残差拟合的线性搜索，多元GBDT分类和二元GBDT分类以及GBDT回归算法过程相同。
GBDT算法梳理
参考自：gbdt算法 GBDT全称Gradient Boosting Decison Tree，同为Boosting家族的一员，它和Adaboost有很大的不同。Adaboost 是利用前一轮弱学习器的误差率来更新训练集的权重，这样一轮轮的迭代下去，简单的说是Boosting框架+任意基学习器算法+指数损失函数。GBDT也是迭代，也使用了前向分布算法，但是弱学习器限定了只能使用CART回归树模型，同时迭代思路和Adaboost也有所不同，简单的说Boosting框架+CART回归树模型+任意损失函数。 GBDT的思想可以用一个通俗的例子解释，假如有个人30岁，我们首先用20岁去拟合，发现损失有10岁，这时我们用6岁去拟合剩下的损失，发现差距还有4岁，第三轮我们用3岁拟合剩下的差距，差距就只有一岁了。如果我们的迭代轮数还没有完，可以继续迭代下面，每一轮迭代，拟合的岁数误差都会减小。
一、前向分布算法
对于AdaBoost，可以将其视为一个将多个弱分类器线性组合后对数据进行预测的算法，该模型可以表示为：
这个公式展现了AdaBoost算法的核心过程。
我们可以利用前向分布算法来求解上一个式子的最优参数。前向分布算法的核心是从前向后，每一步计算一个基函数及其系数，逐步逼近优化目标函数式，就可以简化优化的复杂度。 M-1个基函数的加法模型为：
二、负梯度拟合
Freidman提出了梯度提升算法，算法的核心是利用损失函数的负梯度将当前模型的值作为回归问题提升树算法中的残差的近似值，去拟合一个回归树。 GBDT的思想就是不断去拟合残差，使残差不断减少。用一个通俗的例子来讲假如有个人30岁，我们首先用20岁去拟合，发现损失有10岁，这时我们用6岁去拟合剩下的损失，发现差距还有4岁，第三轮我们用3岁拟合剩下的差距，差距就只有一岁了。如果我们的迭代轮数还没有完，可以继续迭代下面，每一轮迭代，拟合的岁数误差都会减小。（参考集成学习之Boosting-gbdt）GBDT中每次迭代构造的Cart树都是用前一轮的残差拟合的。 第t轮第i个样本的损失函数的负梯度表示为：
利用(x_i, r{ti}) (i=1,2,...,m)我们可以拟合一颗CART回归树，得到了第t颗回归树，其对应的叶节点区域R{tj}, j=1,2,...,J其中J为叶子节点个数。 针对每一个叶子节点里的样本，我们求出使损失函数最小的 输出值c_{tj}: [图片上传失败...(image-d926ad-1565401743253)]
三、损失函数
四、回归
五、二分类，多分类
六、正则化
七、优缺点
优点：
可以灵活处理各种类型的数据，包括连续值和离散值
相对于SVM来说，较少的调参可以达到较好的预测效果
使用健壮的损失函数时，模型鲁棒性非常强，受异常值影响小
缺点: 由于弱学习器之间存在依赖关系，难以并行训练数据
八、sklearn参数
boosting框架相关参数：
n_estimators：弱学习器最大迭代次数/弱学习器个数 learning_rate：每个弱学习器的权重缩减步长（正则化时的a） subsample：子采样比例 init：初始化时的弱学习器，默认用训练集样本来做样本集的初始化分类回归预测
loss：损失函数
分类模型：对数似然损失函数deviance，指数损失函数exponential 回归模型：均方差ls，绝对损失lad，Huber损失huber，分位数损失quantile
alpha：只有回归模型有，当使用Huber损失和分位数损失时指定的分位数的值
弱学习器参数：
max_features：划分时考虑的最大特征数 max_depth：决策树最大深度 min_samples_split：内部节点划分所需最小样本数 min_samples_leaf：叶子节点最少样本数 min_weight_fraction_leaf：叶子节点最小样本权重，若小于改值则该节点会和兄弟节点一起被剪枝 max_leaf_nodes：最大叶子节点数 min_impurity_split：节点划分最小不纯度
九、应用场景
GBDT的适用面非常广，几乎可以用于所有回归问题（线性/非线性），也可以用于分类问题。