62. Unique Paths

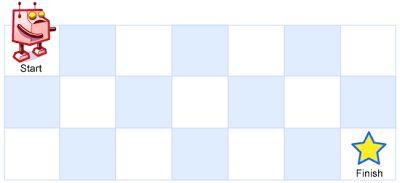
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?

Above is a 3 x 7 grid. How many possible unique paths are there?
Note: m and n will be at most 100.

Solution1：DP

思路：
Time Complexity: O(mn) Space Complexity: O(mn)

Solution2：DP with space optimization

思路：
Time Complexity: O(mn) Space Complexity: O(2n)

Solution3：DP with space optimization

思路：
Time Complexity: O(mn) Space Complexity: O(n)

Solution1 Code：

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        
        for(int i = 0; i < m; i++){
            map[i][0] = 1;
        }
        for(int j = 0; j < n; j++){
            map[0][j] = 1;
        }
        
        for(int i = 1; i < m; i++){
            for(int j = 1; j < n; j++){
                map[i][j] = map[i - 1][j] + map[i][j - 1];
            }
        }
        return map[m - 1][n - 1];
    }
}

Solution2 Code：

class Solution {
    public int uniquePaths(int m, int n) {
        if (m < n) return uniquePaths(n, m); // keep n smaller for less memory usage
        int[] pre = new int[n];
        int[] cur = new int[n];
        
        Arrays.fill(pre, 1);
        /*
        for(int i = 0; i < n; i++) {
            pre[i] = 1;
        }
        */
        cur[0] = 1;
        
        // dp starts     
        for(int i = 1; i < m; i++) {
            for(int j = 1; j < n; j++) {
                cur[j] = cur[j - 1] + pre[j];
            }
            int[] tmp = pre;
            pre = cur;
            cur = tmp;
        }
        return pre[n - 1];
    }
}

Solution3 Code：

class Solution {
    public int uniquePaths(int m, int n) {
        if (m < n) return uniquePaths(n, m); // keep n smaller for less memory usage
        
        int[] row = new int[n];
        
        Arrays.fill(row, 1);

        // dp starts     
        for(int i = 1; i < m; i++) {
            for(int j = 1; j < n; j++) {
                row[j] += row[j - 1];
            }
        }
        return row[n - 1];
    }
}