62. Unique Paths

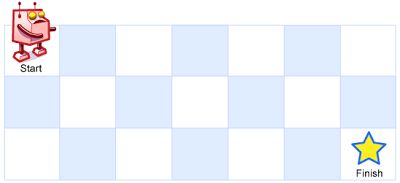
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

image

Above is a 3 x 7 grid. How many possible unique paths are there?

Note:
m and n will be at most 100.

思路

1. 用DP来做，因为机器只能向右或者向下走。用pathNum[i][j]表示机器人从起始位置[0, 0]，走到当前点的一共有多少种走法。那么，pathNum[i][j] = pathNum[i - 1][j] + pathNum[i][j - 1]
2. 初始值，数据的第一列和第一行值都为1，因为第一行机器人只能向右走，那么只有一条路可以走到它。同理，第一列机器人也只能向下走，也只有一条路可以走到它。

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] pathNumber = new int[m][n];
       // pathNumber[0][0] = 0;
        
        for (int i = 0; i < m; i++) {
            pathNumber[i][0] = 1;
        }
        
        for (int i = 0; i < n; i++) {
            pathNumber[0][i] = 1;
        }
        
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                pathNumber[i][j] = pathNumber[i][j - 1] + pathNumber[i - 1][j];
            }
        }
        return pathNumber[m - 1][n - 1];
    }
}