qbxt Day 2 afternoon
——2020.1.18 济南 主讲:李佳实
目录一览
1.线段树
2.二叉搜索树(略过)
3.树状数组
总知识点:基础数据结构(本人初学感觉好难)
一、线段树
1.描述:线段树是一种分治的思想,用树形结构把一个大区间划分成小区间,它同时又是一棵二叉树。
2.概念名词定义:
区间(又称线段):线段树上的每一个节点对应于一个区间[a,b]。(a,b为整数)
特殊说明:对于叶子节点,其对应的区间长度为1。
For Example:
(1)区间[1,10]对应的线段树
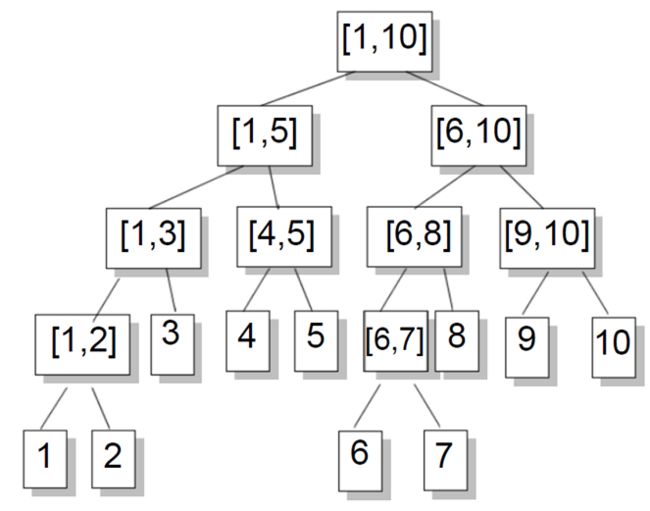
3.性质:对于每一个非叶结点所表示的结点[a,b],其左儿子表示的区间为[a,(a+b)/2],右儿子表示的区间为[(a+b)/2+1,b](除法去尾取整)
4.基本操作:
(1)线段树的存储:类似于堆
对于一棵线段树,它的根节点下标为1。
其下标为i的节点,它的左儿子下标为2i,右儿子下标为2i+1。
(2)线段树核心操作:区间分解
定义:若线段树根节点对应区间为[a,b],给定区间c,d,找出一些节点,使这些节点对应的区间互相不重叠,且加起来正好是[c,d],这样的操作过程即区间分解。
代码核心思想:二分
操作步骤:(递归分解)
1.从根节点出发,开始区间分解
2.遇到节点[x,y]时,如果要分解的区间就是[x,y],即为找到一个终止节点,Break。
3.否则,(二分思想)定义mid,取mid=(x+y)/2。
4.看我们要分解的区间与[x,mid]和[mid+1,y]和哪个有交集,就进入区间进行进一步的递归分解。(有可能与左右两个区间都有交集,需要同时分解)
注:区间分解的时间复杂度和分解完以后的区间个数均为O(logn)。
For Example:区间[1,9]的线段树上,分解区间[2,8].
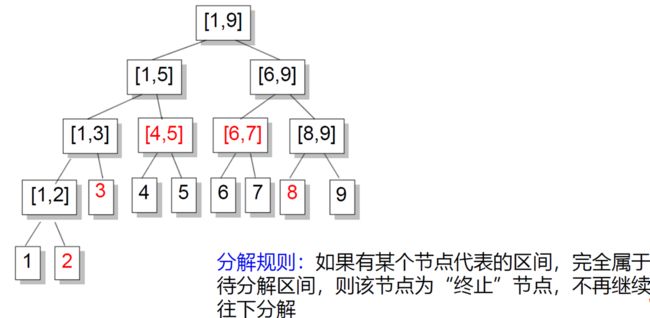
代码实现:
inline void spilt(int k,int l,int r,int z,int y){
//k为当前节点的编号
//l,r为线段树的总区间。z,y为要分解的目标区间[z,y]
if(l==z&&r==y) return; //找到了一个分解的区间
int mid=(l+r)/2;
if(y<=mid) spilt(k*2,l,mid,z,y); //在左儿子的区间里,分解左儿子的区间
else if(z>mid) spilt(k*2+1,mid+1,r,z,y); //在右儿子的区间里,分解右儿子的区间
else{ //两个区间都有交集
spilt(k*2,l,mid,z,mid); //目标区间在左儿子里的部分
spilt(k*2+1,mid+1,r,mid+1,y); //目标区间在右儿子里的部分
}
}
//例:(上图)spilt(1,1,9,2,8) 二、二叉搜索树:本内容主要为了以后学习平衡树Tree,暂且略过。。。。。。(勿喷)
三、树状数组:(心碎的回忆)
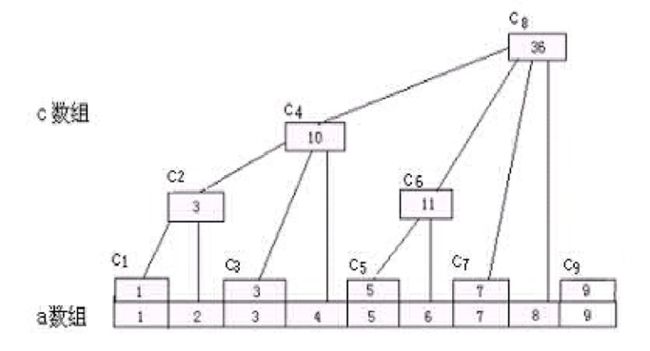
1.定义:
For Example:
以56为例:56->111000
K=3
56-2^3+1=(110001)(二进制)=49
C[56]=a[49]+..+a[56]
a[1...56]=C[56]+C[48]+C[32]
注:A是原数组、C是树状数组。
3.执行操作:单点修改、区间查询
4.(玄学操作)lowbit
2^k=lowbit(x)=x and (x xor(x-1))
For Example:
假设:
x = 0...1...0...10......0(第二个1后k个0)
x = 0...1...0...01......1(第三个0后k个1)
则
x xor(x-1)=0...0...0...11......1(第一个1后k+1个1)
5.查询操作
代码:
int query(int x) //求a[1...x]的和
{
int res=0;
for(int i=x;i>0;i-=lowbit(i)) res+=C[i];
return res;
}6.修改操作
代码:
```c++
void add(int x,int delta) //将a[x]添加delta
{
for(int i=x;i<=n;i+=lowbit(i)) C[i]+=delta;
}