Electronic Potentials and Fields:
Laplace's Equation
Abstract
We are going to use Laplace's Equaton to discribe the electronic fields. When giving the boundry conditions, we can solve the equation so that we can get the each point in the field.So there are some simple examples we have discussed.
Background and Approximation
In electromagnetism, electromagnetic field is a kind of a physical field produced by a charged object in the electromagnetic field of a charged object will feel the force of electromagnetic field。In regions of space that do not contain any electronic charges, the electric potential obeys Laplace's equation:
A simple equation, but the simulation is not that simple:
at the point(i,j,k) the derivative with respect to x may be written as
Then we can write as
Thus, write the second partial derive as
where the notation here is intended to indicate that the derivatives are to be evaluated at the locations(i+_1), this leads to
Main Body
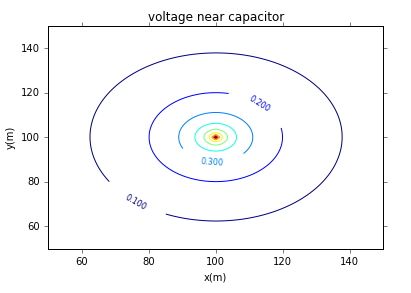
Ftrst, we discuss the solution of the capacitor electric potential field around.
The parameters an be found on the picture.We use the boundry condition to solve the equation
Here is the code .
Thenwe can find that Uniform distribution of electric field between the poles, and accord with the theoretical value.
Then we can discuss the electric particle.
Here is the code_1 and code_2
And we can see the field lines in the picture.
We can find that potential centered on the charge of concentric circles, and the electric field lines radiating/
Conclusion
As we discussed above, we can find that the simulation is the same as we studied in the electromagnetism. That confirmed our approximation is effective in this electronic field problem.
Acknowledgements an References
Thanks for the shared code from WuYuqiao