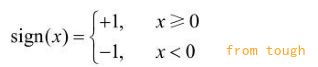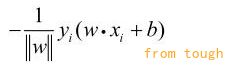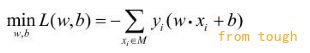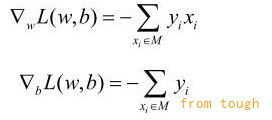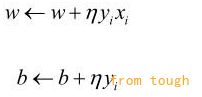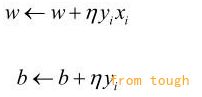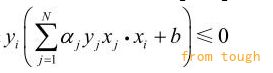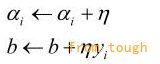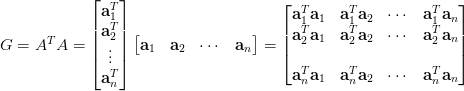感知机
概述
感知机是二类分类的线性分类模型,其输入为实例的特征向量,输出为实例的类别,取+1和-1二值。感知机学习旨在求出将训练数据进行线性划分的分离超平面,为此,导入基于误分类的损失函数,利用梯度下降法对损失函数进行极小化,求得感知机模型。它是神经网络与支持向量机的基础。
感知机模型
假设输入空间(特征空间)是x∈Rn,输出空间是y={+1,-1}。输入是实例的特征向量,对应于输入空间的点;输出是实例的类别。输入空间到输出空间的如下函数:
f(x) = sign(w*x + b)
称为感知机。sign是符号函数,即:
感知机模型如下:
数据集的线性可分性
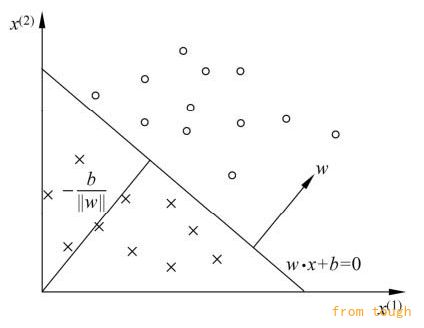
给定一个数据集,如果存在某个超平面S:w*x+b,能够将正实例点和负实例点完全正确地划分到超平面的两侧,则称数据集T为线性可分数据集;否则,数据集T为线性不可分
感知机学习策略
假设训练数据集是线性可分的,感知机学习的目标是求得一个能够将训练集正实例点和负实例点完全正确分开的分离超平面 它选择的损失函数是误分类点到超平面S的总距离
输入空间中任一点x0到超平面S的距离是:
这里,||w||是w的L2范数。
-----------补充(数学知识):------------
一、一般平面方程
二、点法式
假设平面
经过一定点
且其法线向量为
,下面来建立平面方程
设点是平面上任一点(图6-17)。则向量必与平面的法线向量垂直,于是,而,,所以
(1)
这就是平面上任一点的坐标所满足的方程
二、点到平面的距离公式回顾:(主要就是面上一点和该点连线在发方向上的投影啦)
在平面上任取一点
,并作一法线向量
,考虑到
与
的夹角
也可能是钝角,得所求的距离
设为与向量方向一致的单位向量,那么有
所以
由于
所以
由此得到点到的距离公式:
------------------继续-----------------
对于误分类数据(xi, yi)来说,总有:
-yi(w*xi+ b) > 0
因此,误分类点xi到超平面S的距离是:
那么所有误分类点到超平面S的总距离是:
不考虑1/||w||,就得到感知机学习的损失函数。
感知机损失函数
一个特定样本点的损失函数:在误分类时是参数w,b的线性函数,在正确分类时是0.因袭,对给定的数据集,损失函数L(w,b)是w,b的连续可导函数。
感知机学习方法
感知机学习算法的原始形式
感知机学习算法是以下问题的最优化算法:给定一个训练数据集,求参数w,b,使其为以下损失函数极小化问题的解:
其中M为误分类点的集合。
感知机学习算法是误分类驱动的,具体采用孙吉梯度下降法。首先,任意选取一个超平面w0,b0,然后采用梯度下降法不断地极小化目标函数。极小化过程中不是一次使M中所有误分类点的梯度下降,而是随机选取一个误分类点使其梯度下降。
损失函数L(w,b)的梯度:
随机选取一个误分类点(xi, yi),对w,b进行更新:
式中η(0<η≤1)是步长,统计学习中又叫做学习率。
感知机学习算法原始形式总结:
输入:训练数据集T;学习率η。
输出:w,b;感知机模型f(x)=sign(w*b+b)
1. 选取初始值:w0,b0
2. 在训练集中选取数据(xi, yi)
3. 如果yi(w*xi+ b) ≤ 0:
4. 转至2,直到训练集中没有误分类点
感知机学习算法由于采用不同的初值或选取不同的误分类点,解可以不同。
当训练集线性可分时,可证明该算法收敛(这里证明过程省略);当训练集线性不可分时,感知机学习算法不收敛,迭代结果会发生震荡。
感知机学习算法的对偶形式
对偶形式的基本想法是,将w和b表示表示为xi和标记yi的线性组合的形式,通过求解其系数而求得w和b。
在上述算法中,可假设初始值w0,b0均为0。对误分类点(xi, yi)通过:
逐步修改w,b,设修改n次,则w,b关于(xi, yi)的增量分别是αiyixi和αiyi,这里αi=niη。最后学习到的w,b可以分别表示为:
当η=1时,表示第i个实例点由于误分而进行更新的次数。
感知机学习算法对偶形式总结:
输入:线性可分的数据集T;学习率η
输出:α,b;感知机模型:
其中α=(α0,α1,…,αN)T
1. α<-0,b<-0
2. 在训练集中选取数据(xi, yi)
3. 如果:
那么:
4. 转至2直到没有误分类数据
对偶形式中训练实例仅以内积的形式出现。可以预先将训练集中实例间的内积计算出来并以矩阵的形式存储,这个矩阵就是所谓的Gram矩阵:G = [xi▪xj]NxN。
Gram 矩阵就是说A=(x1,x2,x3)
Gram=AA*(A*是A的转置向量)
在线性代数中,内积空间中一族向量。
的格拉姆矩阵(Gramian matrix 或 Gram matrix, Gramian)是内积的对称矩阵。
设
为一个
实矩阵,
方阵
称 Gramian 或 Gram 矩阵,也有人称之为交互乘积 (cross-product) 矩阵。考虑
的行向量表达式
,
,则