萌新一枚,有错还请大佬们指教> <
氢原子层面上:
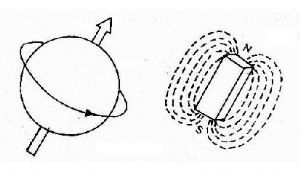
氢原子的运动特性为:做自旋运动的同时围绕一个旋转轴(该方向产生的磁矩为净磁矩)旋转。情况如图1-1所示:
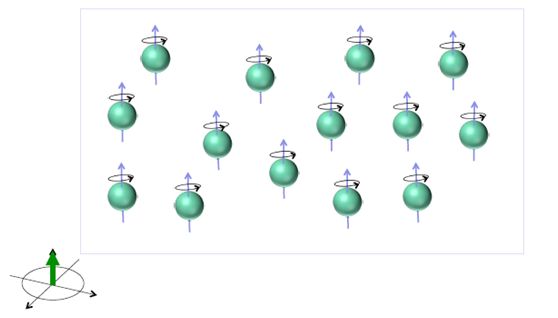
当无外界强磁场作用的情况下,脑内所有的氢原子自旋所绕的旋转轴方向随机。故宏观看来,对外净磁矩为0。
因此平衡状态下,会产生一个与B0方向的相同的磁化M0 (magnetization),这个M0就是MRI信号的来源。如图1-2所示:
这时,施加一个RF脉冲(实质上是一个在xy平面中旋转的磁场B1,让B1也沿着以拉莫频率旋转)。由于共振特点,氢原子会吸收能量跃迁变轨,氢原子在自旋的同时以B1为旋转轴旋转。所有的氢原子叠加共同产生一个与B1同方向(不断旋转)的净磁矩。
这个B1与B0夹角为90度,称为90度脉冲,此时移除B1,x-y平面的磁化为Mxy,其大小与M0相同, z轴方向的磁化为Mz,其大小为0。
一般来说,有两种常用的脉冲,90度脉冲和180度脉冲。180度脉冲会将纵向磁化矢量转向到M0的反方向;失相质子在XY平面内翻转180度。两种脉冲的差异如图1-3所示:
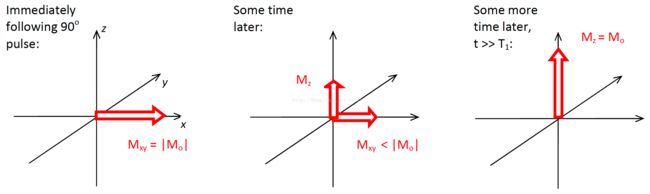
当B1被移除,氢原子放能,重新在B0的作用下逐渐恢复到原来的平衡状态,这个过程称为弛豫(relaxation), 具体表现为两方面:Mxy逐渐恢复为0,Mz逐渐恢复到M0。总体变化状态如图1-4所示:
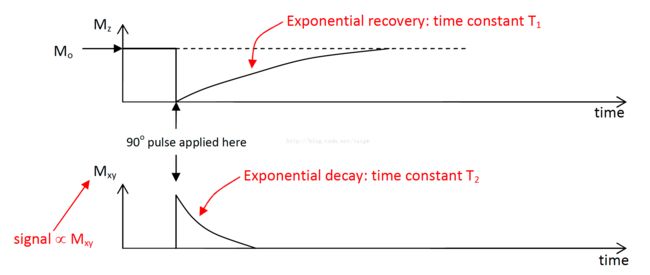
Mz方向上,净磁矩成指数形式增长,而Mxy方向上,成指数形式衰减。两个方向上变化函数如图1-5所示:
然而,只有当B0处处相等,所有的氢原子的拉莫频率才会相同。而只有这时,才能保证当B1存在时,所有氢原子都和B1以相同频率一起转动。
在实际情况下,无法保证B0处处相等,因此在B1施加的过程中,所有氢原子旋转轴所处的相位并不相同,这就低估了Mxy的最大值,因此实际测量的T2*比理想情况下的T2小。
成像层面上:
MR信号本质
这时可能有一个问题:那我们采集的MR信号具体是什么信号呢?
实际上,MRI中的信号采集线圈就是测量Mxy的,如果Mxy的大小为0,就没有信号输出。这就是为什么T2*与T2的差异需要我们格外在意了。
K空间
要了解成像是怎么形成的,我们需要了解以下K空间的概念:
其实K空间是涉及到傅立叶变换的一个概念,在介绍K空间之前,先简单介绍一下傅立叶变换,一维空间上的傅立叶变化如图2-1所示。
对三个不同频率的正弦波进行线性叠加,叠加时每一个都乘以一个系数(在这个例子中,第一个乘以0.5,第二个乘以2,第三个乘以1),而等号下面的图片则显示了线性叠加后的结果在时域(time domain)中的形态。其右侧的图片显示了傅立叶变换后的结果,也即正弦波的叠加在频域(frequency domain)中的表示。图中的三个峰分别代表这三个叠加起来的正弦波,三个峰的横坐标分别代表这三个正弦波的频率,而其纵轴坐标则代表线性叠加时乘上的系数,也即成上系数后相应的正弦波的波幅(第一个峰的高度为0.5,第二个为2,第三个为1)。
实际上可以简单地理解成:傅立叶变换实质上就是把各种频率波从复杂信号中分离出来的变换方法。变换后,信号从时间-强度坐标系转到了频率-强度坐标系。
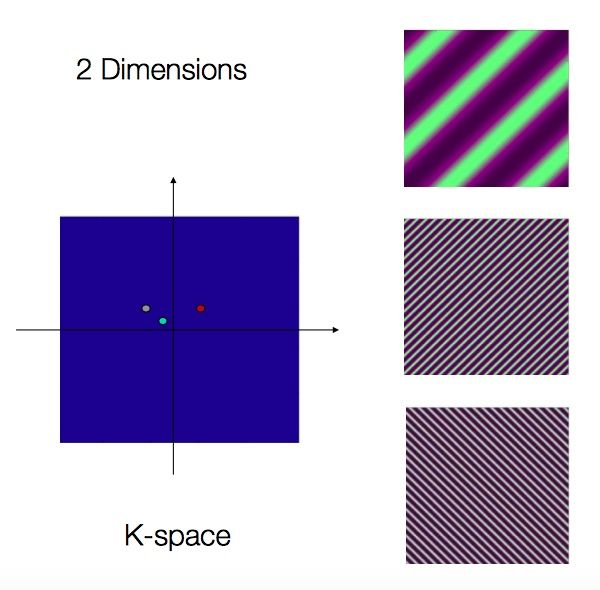
对于二维的波,我们同样可以进行分解,例如图2-2中左图的3个点就代表了二维空间上三种不同的波,需要注意的是,左图上的两个坐标轴表示空间X轴上的频率值和Y轴上的频率值,这就是K空间。
根据上面的描述,我们已经可以提炼出K空间的特性了:
K空间可以把复杂的波形图像简单化,抽象成频率空间内的一个点。
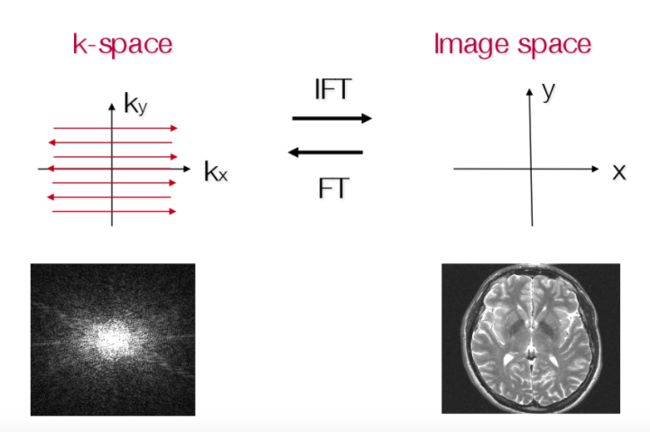
那么我们一定会问:平时常见的MR图像在K空间长什么样子呢?图2-3中给出了对应关系,右图实际上就是左图中点所代表的波的叠加。
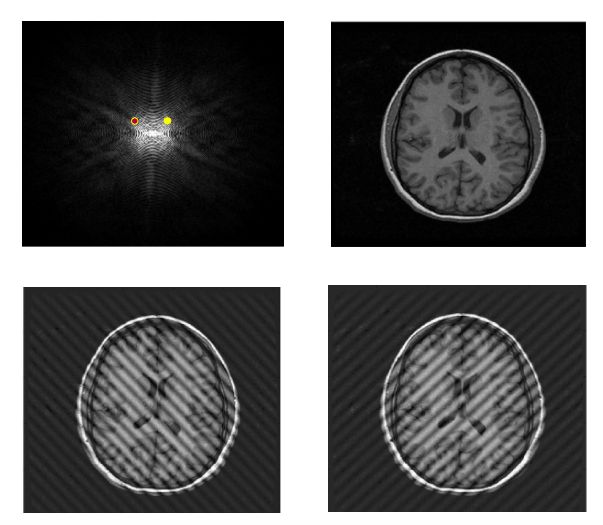
为了更加清晰的阐述,我们可以从图7中剔除几个K空间上的点,看看图像的变化。如图2-4所示,剔除红点和黄点给图像带来了以下变化:
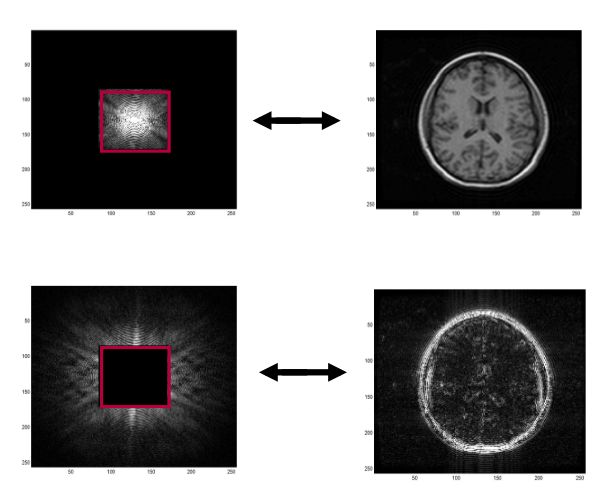
我们再来考察去除高频或低频成分会发生什么。我们知道,K空间中越远离原点的位置,所代表的正弦波的频率越高。如图9,当我们删除K空间中远离原点位置的那些数据时(图2-5上两张),逆傅立叶变换得到的图像能够比较好地显示大脑剖面图的样子,只是变得有些模糊,分辨率不够高。而当我们删除K空间中原点附近位置的数据时(图2-5下两张),逆傅立叶变换得到的则是关于结构边界的细节。左上、左下两张图的叠加,可以恢复原来的K空间中的数据;而右上、右下图的叠加,则可以恢复原来的图像空间中的数据。
由此我们可以看出,图像空间中的图像分辨率与K空间中的数据点数量密切相关。K空间中有多少数据点,图像空间中也就能还原出多少个数据点;K空间中有越多的数据点,图像的空间分辨率也就越好。
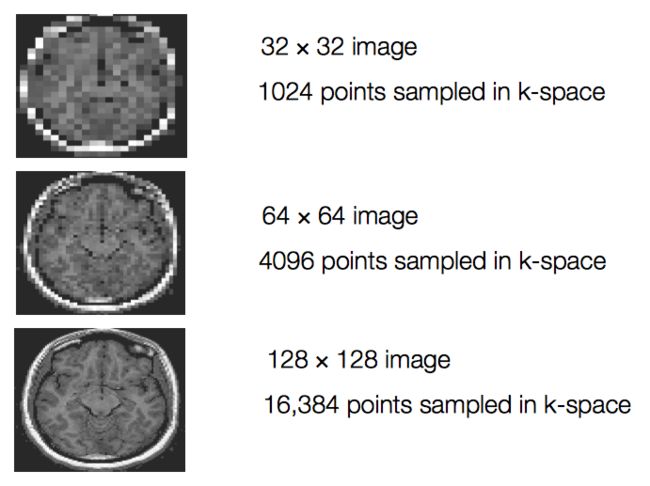
图2-6给出了几个K空间数据点个数语图像空间中图像分辨率的关系。
当K空间中有1024个数据点时,我们可以还原出32 ×32的图像;
当K空间中有4096个数据点时,可以还原出64 ×64的图像;
当K空间中有16348个数据点时,可以还原出128 ×128的图像……
然而我们又知道,要想在K空间中取更多的数据点,就必须进行更多次的测量,也就要耗费更长的时间。因此,要想提升图像空间分辨率,就必须付出降低时间分辨率的代价。在实际工作中,我们应当根据要研究的问题,找到时间分辨率和空间分辨率的平衡。
从图像整体到局部
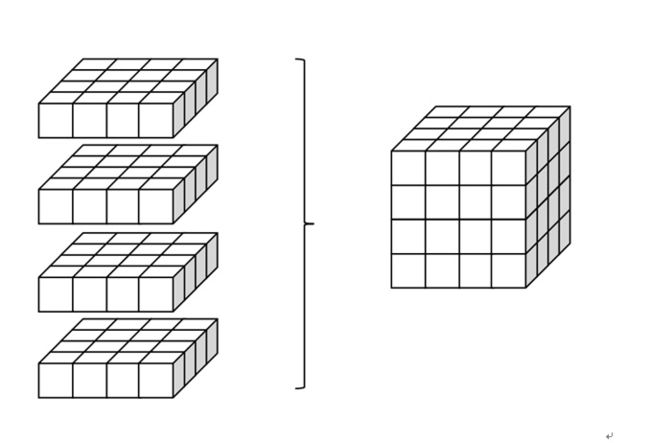
脑成像信号采集对应的单位是体素,实际上就是把一个脑子切成若干片,每一片又切成若干小块,每一块就是一个体素,如图2-7所示。我们想要获取的,是每个体素中的质子浓度(也就是每个体素中独特的MR信号)。
当我们直接对整个脑子的信号进行无差别提取的时候,我们直接测量到的值来自于整片脑区域所含的氢原子,而我们更希望独立的测量到每个体素所含的氢原子的数量。此时我们就需要另外一个磁场了,我们将其称为梯度磁场(magnetic field gradient),通过梯度磁场我们可以得到一个关于氢原子浓度的加权积分。具体求解见公式2,其中的S(kx,ky)实际上是在K空间下,(kx,ky)坐标的值,也就是该频率下的振动权重。
注:由于磁场在空间中沿着X轴和Y轴梯度变化,所以需要考虑(kx x+kyy)项。
如果我们能获得多个S(Kx,Ky),就可以用逆向傅立叶变换求出每个点的氢原子数量ro(x,y)。
根据线性方程求解的原理,我们知道,要得到N个未知数的解,最少要有N个方程。
因此,要得到分辨率为nn的图像,我们至少要测量nn个S值。
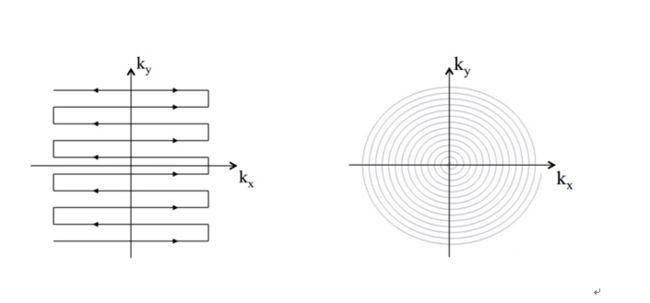
一般来说,为了得到这若干个S值,我们在K空间中取多个点进行测量。常见的方法有EPI(回波平面成像),SI(螺旋成像)。如图2-8所示,两种方法的差异主要体现在他们的取点路径上。
MRI常用脉冲序列及应用
基本概念:
- 脉冲序列(pulse sequence):具有一定带宽、一定幅度的射频脉冲与梯度脉冲组成的脉冲程序。
- 重复时间(TR):脉冲序列重复时间,即前一脉冲序列和相邻的后一脉冲序列之间的时间间隔。单位ms。
- 回波时间(TE):脉冲至采集信号峰值之间的时间间隔。
学习过程中发现前面说到的T1,T2和这里的TR,TE的关系很容易混淆,所以这里写下我的理解:
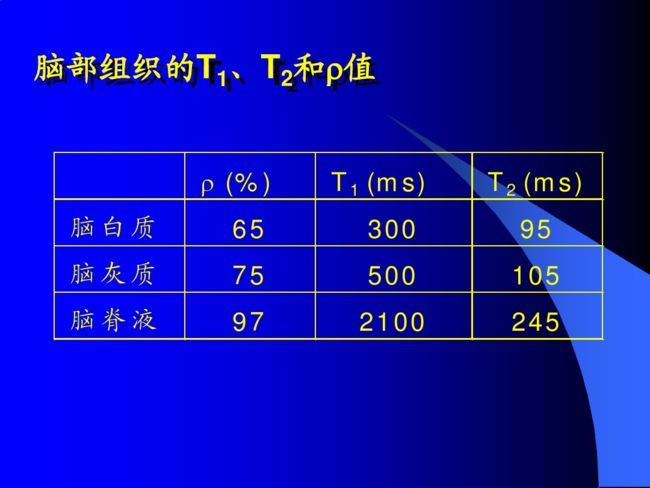
首先我们要明确,T1、T2是由质子所处的组织属性决定的。不同的组织弛豫时间有所不同,例如脂肪的T1弛豫较短,而脑脊液的T1弛豫较长。见图3-1。
TR和TE是人为设置的:
TE决定了在信号(信号就是Mxy)读出前,Mxy上的衰减量。因此我们可以说,TE决定了所读出的T2弛豫量。
较短的TR下,脑脊液也许还没有完成向M0的恢复,但脂肪已经完成了。在下一次脉冲到达时,脑脊液只要吸收较少的能量就能达到饱和,而脂肪却要吸收较大的能量。在这个意义上,较短的TR和TE可以区分不同的组织,因为他们决定了T1弛豫的程度。
那么我们所说的加权又是什么意思呢?这和TR、TE长短对T1、T2差异对比度的影响有关,图我已经看昏了,不如看看公式3,这就是我们测量到的信号(怎么算的就不要为难我胖虎了):
这里需要补充,TR是肯定大于TE的,所以我们要明确,当TE长的时候,TR不可能短。
图3-2写明了各种加权成像的TR、TE特点:
那么脉冲序列又是什么东西呢?在实际应用中,不同的脉冲序列也各有千秋。具体可参考下图(感谢华西!)
具体的序列我看懂再写。。。
然后下次会写一点空间转换的东西。
参考:
https://zhuanlan.zhihu.com/p/22172325
https://zhuanlan.zhihu.com/p/22208517
https://blog.csdn.net/taigw/article/details/44834953