动态规划 || 最长子序列

相同子序列的定义

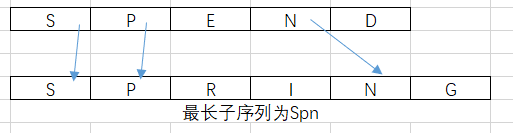
有两个字符串S1和S2，在从左往右的顺序中，有相同元素组成的序列，称为相同序列。必须强调的是：序列是不要求元素连续的。如下图所示：

Spring和Spend的子序列是：SPN

 

 

 

解决思路

通过动态规划来完成题目。首先，要使用动态规划要明确转移方程是什么，而转移方程需要对问题的理解和抽象才能得出。一般来说，动态规划也需要把问题分解为子问题，但不同于递归的分解过程是互不影响的，动态规划往往需要前面的结果来决定后面的策略。同时，为了减少不必要的计算，所以通常需要一个记录的容器来记录子问题的最优解，从而扩展为全局最优解。

从题目上看：

1. 第一种情况：若当前的字符串S1与S2的最后一个元素相同，则可以分解为：S1的前m-1的元素与S2的前n-1个元素的最长子序列+1。
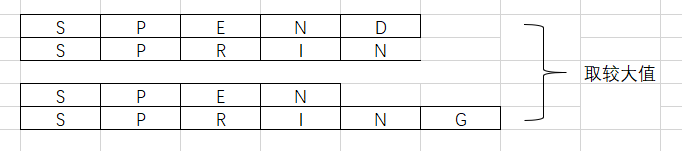
2. 第二种情况：若当前的字符串S1与S2的最后一个元素不相同，则可以分解为：比较S1的前m-1的元素与S2 或者 S1与S2的前n-1个元素之间的较大值。如下图所示：

 

 

 

 因此，可以得出以下的的转移方程：

 其中：C是存储子结果的数组，i和j分别是字符串S1和S2的下标。

过程解析

下面通过图解案例的方式来说明：

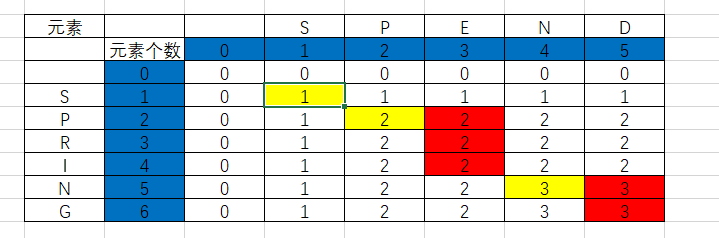
如图所示,在算法还没开始的状态，可以得知当字符串S1或S2的元素个数为0时，他们的最长子序列一定是0。

 

接下来，从以Spend为参照对象，以Spring为比较对象，从Spring开始填表。

 

 从表中看出，Spring的第一个元素“S”与比较对象Spend的第一个元素相等，套用转移方程：C[i-1][j-1]+1，即c[1][1]=0+1。

而元素“S“与Spend的后面元素比较都不相等，则套用转移方程：c[1][2] = Max(C[i-1][j],C[i][j-1])即max(0,1)，所以c[1][2]还是等于1。

还有一个特殊的点是c[2][2]，从上表可以得出，S1[2]和S2[2]的元素都为”P“，所以满足条件S1[i]==S2[j]，所以可以得出c[2][2]的值为：c[1][1]+1 = 2。

根据上面的解析，可以把表填充完整如下图所示：

 

 

 那么我们要求的最长子序列的长度就是c[m][n]，也就是二维数组的右下角的值。

 而具体的代码我也在下面贴出

 1 public class Solution {
 2 
 3     public static void main(String[] args) {
 4         String str1 = "Spring";
 5         String str2 = "Spend";
 6         char[] s1 = str1.toCharArray();
 7         char[] s2 = str2.toCharArray();
 8 
 9         //设定一个二维数组存放当前的最长公共子序列，如前i个s1元素与前j个s2元素有多少个公共子序列元素
10         int[][] c = new int[s1.length+1][s2.length+1];
11         /*
12          * 根据转移方程:若s1[i]==s2[i]
13          * c[i][j] = c [i-1][j-1]+1
14          * 若s1[i]!=s2[i]
15          * c[i][j] = max(c[i][j-1] , c[i-1][j]  )
16         **/
17         for (int i =1;i<=s1.length;i++){
18             for (int j=1;j<=s2.length;j++){
19                 if (s1[i-1] == s2[j-1]) {
20                     c[i][j] = c [i-1][j-1]+1;
21                 }else {
22                     c[i][j] = Math.max(c[i][j-1] , c[i-1][j] );
23                 }
24             }
25         }
26     }
27 }

 

求出一个最长子序列

在上面已经求得存放比较结果的数组，如果题目要求输出一个最长子序列，那么可以根据这个数组来还原。

还原的策略如下：

1. 当前元素相等，保存元素，同时缩减i和j
2.  元素不相等，往c值较大的方向缩减，若左边和上方的值相等，则往上边缩减（也可以往左边缩减）。
3. 当字符串的索引i或者j到达0时，停止缩减。

如图所示：

 

完整的代码如下

public class Solution {

    public static void main(String[] args) {
        String str1 = "Spring";
        String str2 = "Spend";
        char[] s1 = str1.toCharArray();
        char[] s2 = str2.toCharArray();

        //设定一个二维数组存放当前的最长公共子序列，如前i个s1元素与前j个s2元素有多少个公共子序列元素
        int[][] c = new int[s1.length+1][s2.length+1];
        /*
         * 根据转移方程:若s1[i]==s2[i]
         * c[i][j] = c [i-1][j-1]+1
         * 若s1[i]!=s2[i]
         * c[i][j] = max(c[i][j-1] , c[i-1][j]  )
        **/
        for (int i =1;i<=s1.length;i++){
            for (int j=1;j<=s2.length;j++){
                if (s1[i-1] == s2[j-1]) {
                    c[i][j] = c [i-1][j-1]+1;
                }else {
                    c[i][j] = Math.max(c[i][j-1] , c[i-1][j] );
                }
            }
        }

        //根据数组倒推出子序列
        StringBuilder result =new StringBuilder();
        int i = s1.length;
        int j = s2.length;
        while (i>0 && j>0){
            //当前元素相等，保存元素，同时缩减i和j
            if (s1[i-1] == s2[j-1]){
                result.insert(0,s1[i-1]);
                i--;j--;

            }else{
                //元素不相等，往c值较大的方向缩减，若左边和上方的值相等，则往上边缩减。
                if (c[i-1][j] >= c[i][j-1]){
                    i--;
                }else {
                    j--;
                }
            }

        }
        System.out.println(result.toString());
    }
}