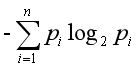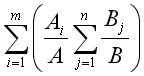输入
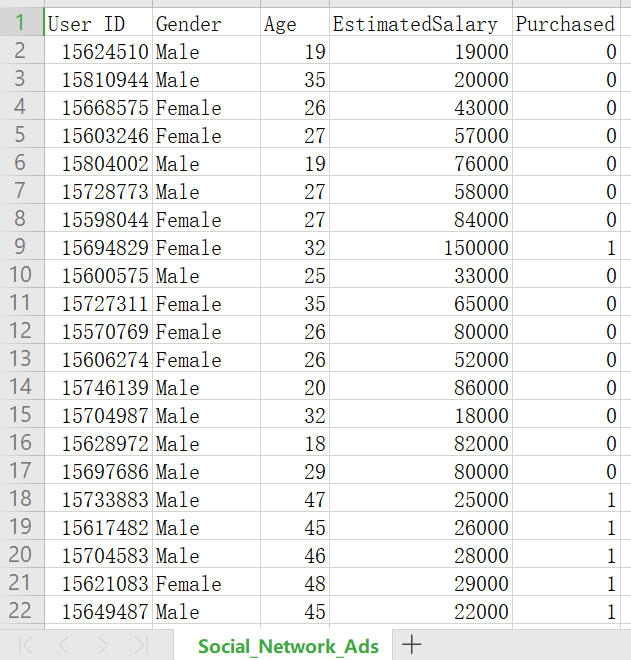
400条用户购买记录,每条记录包含用户id、性别、年龄、薪水、是否购买,具体如下图:
输出
输出1:从输入1中的400条数据中选择一部分作为训练数据,训练得到随机森林模型。
输出2:根据输出1得到的随机森林模型,对从400条输入数据中挑选出来的测试数据进行购买预测,输出模型的准确率。
工具
本文使用工具为:Anaconda、PyCharm、python语言、PySpark
原理
随机森林是由许多决策树构成,是一种有监督机器学习方法,可以用于分类和回归,通过合并汇总来自个体决策树的结果来进行预测,采用多数选票作为分类结果,采用预测结果平均值作为回归结果。
“森林”的概念很好理解,“随机”是针对森林中的每一颗决策树,有两种含义:第一种随机是数据采样随机,构建决策树的训练数据集通过有放回的随机采样,并且只会选择一定百分比的样本,这样可以在数据集合存在噪声点、异常点的情况下,有些决策树的构造过程中不会选择到这些噪声点、异常点从而达到一定的泛化作用在一定程度上抑制过拟合;第二种随机是特征随机,训练集会包含一系列特征,随机选择一部分特征进行决策树的构建。通过这些差异点来训练的每一颗决策树都会学习输入与输出的关系,随机森林的强大之处也就在于此。
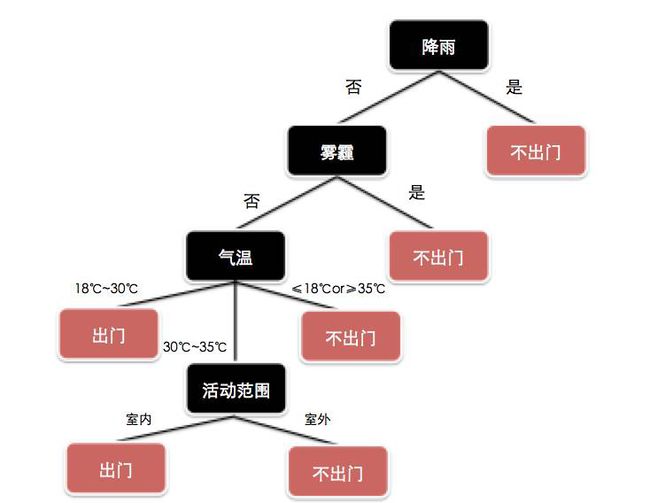
我们主要分析下决策树,首先先进行“顾名思义”,决策树应该是一个树形结构,这个树形结构可以得到一些决策结果,事实上确实如此,决策树的组成成分如下图所示:
其中,根节点与非叶子节点表示一个特征,叶子节点表示类别,节点之间的有向边表示特征的值。
现在你可能会有一个疑问,决策树中的根节点与非叶子节点是如果选择的?这个问题的答案就牵扯到一些数学原理与算法,比如信息熵、信息增益、ID3、信息增益率、基尼系数等,下面就逐一讨论,理解了这些也就搞清楚了决策树的构建过程。
假如有一些数据集:A={1,0,1,0,1,0},B= {1,1,1,1,1,1},C={0,0,0,0,0,0},我们分别从A,B,C三个集合中取出一个数,那么集合A中取出的数就有一些不确定性,这个不确定性就可以用概率表示,假设从数据集A中取出0和取出1的这两个事件是独立的,概率分别记为P0和P1,根据概率论知识P0 = 1/2,P1 = 1/2,那么我们如何进一步来量化数据集A的不确定度呢?这个时候信息熵就可以排上用场了,信息熵可以用来度量信息源的不确定度,具体公式为:
先计算下集合A,B,C的信息熵,熵A = 1, 熵B = 0, 熵C=0。熵越大表明数据集的不确定度越高,数据集越不纯;熵越小表明数据集的不确定度越低,数据集越纯。
当数据集中分类较多的时候,每个类别的概率![]() 较小,但是熵值较大,数据集不确定度越高,纯度越低。
较小,但是熵值较大,数据集不确定度越高,纯度越低。
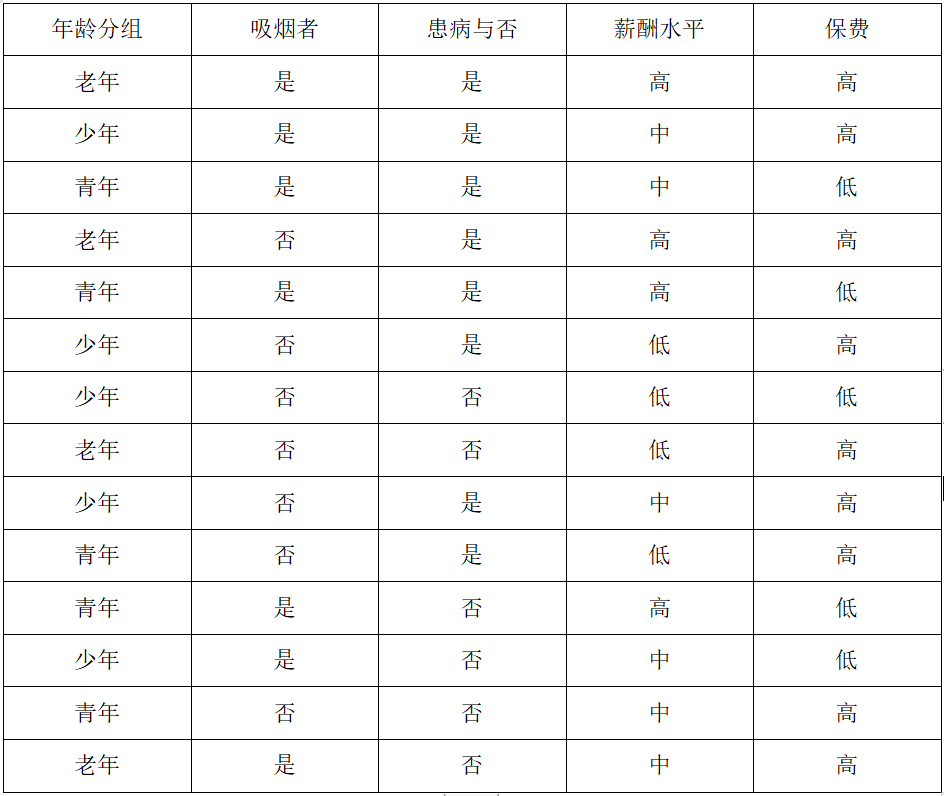
为了尽量降低决策树的高度,我们每次都要尽量选择可以使数据集熵值下降最多的特征作为根节点或者非叶子节点,我们针对下面表格中的数据集进行讨论:
数据集包含四个特征:年龄分组、吸烟者、患病与否、薪酬水平,决策目标为保费。
为了构建决策树,我们需要计算两类熵:
- 目标熵(保费)
- 具有特征的目标熵(例如保费-吸烟者)
为了计算决策目标保费的熵,我们需要计算每一类保费的概率:
高保费类别的概率ph = 9/14 = 0.64,低保费类别的概率pl = 5/14 = 0.36。
代入信息熵计算公式得到:目标熵 = -ph * log(ph) - pl * log(pl) = 0.94 。
下面计算具体特征的目标熵,先给出计算公式:
其中A为数据集的数据量,i为特征的类别,![]() 为某种特征类别的数据量,B为特征类别下的目标数据量,B与
为某种特征类别的数据量,B为特征类别下的目标数据量,B与![]() 相等,j为某特征下的目标类别,
相等,j为某特征下的目标类别,![]() 为某特征类别下某目标类别的数据量。
为某特征类别下某目标类别的数据量。
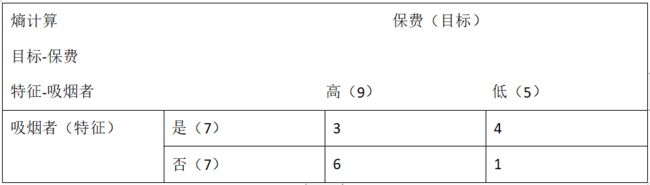
以熵(保费,吸烟者)为例,对于上表的数据集,A=14,吸烟者特征把数据集分为了两类:是吸烟者、不是吸烟者,m = 2,A1 = 7,A2 = 7。在吸烟者类别下,有高、低两种目标数据,j = 2,高保费的数据量B1 = 3,低保费的数据量B2 = 4;在不是吸烟者类别下,也有高、低两种目标数据,j = 2,高保费的数据量B1 = 6,低保费的数据量B2 = 1。具体统计信息如下表所示:
代入计算公式得到:
熵(保费,吸烟者)= 0.79 ,同理可以求得:
熵(保费,年龄分组)= 0.69
熵(保费,患病与否)= 0.89
熵(保费,薪酬水平)= 0.91
计算得到两个信息熵之后,就可以计算信息增益(Information Gain),能够提供最大信息增益的特征将会被用于划分子集,信息增益的计算公式为:
信息增益 = 目标熵 - 熵(目标,特征)
计算各个特征的信息增益:
IG(吸烟者) = 0.94 - 0.79 = 0.15
IG(年龄分组) = 0.94 - 0.69 = 0.25
IG(患病与否) = 0.94 - 0.89 = 0.05
IG(薪酬水平) = 0.94 - 0.91 = 0.03
可以看到年龄分组特征提供了最大的信息增益,所以选择年龄分组作为根节点。根节点确定后,分别对青年、中年、少年三种情况下的三颗子树递归求根节点直至停止并得到叶子节点。
上面我们使用信息增益作为特征选择的标准,该算法也被称为ID3算法,通过ID3算法我们成功的构造了决策树,这种算法虽然简单但是并不能很好的处理某些特殊情况,假设有一个特征变量为ID,具体如下: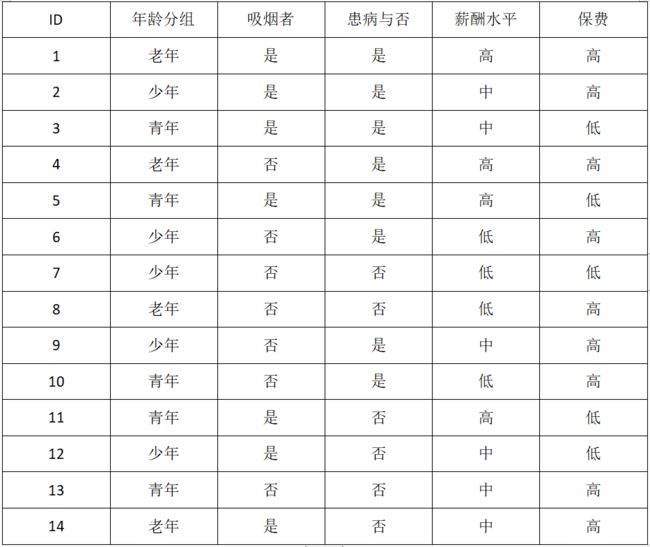
我们计算下特征ID的信息熵:
熵(保费,ID) = -1/14 * log1 + ... + (-1/14 * log1)= 0
特征ID带来的信息增益为:
IG(ID) = 0.94 - 0 = 0.94
特征ID达到了信息增益最大化,但是实际上呢?ID并没有对分类任务起太大作用,这种情况并不总是会发生,但也是会存在一定的概率。
为了改进ID3算法,人们提出了C4.5算法,该算法采用信息增益率作为衡量数据集纯度的标准,信息增益率的计算公式为:
信息增益率 = 信息增益/特征自身的熵
以上面讲的特征ID为例,计算ID自身的熵为: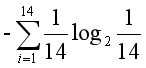 ,这是一个很大的数,这样得到的信息增益率就比较小了。
,这是一个很大的数,这样得到的信息增益率就比较小了。
另外还有一种衡量数据集纯度的标准:基尼系数。基尼系数的计算公式为:
Gini系数 = 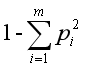 ,其中m为目标的分类数目,
,其中m为目标的分类数目,![]() 为某分类目标的概率。
为某分类目标的概率。
Gini系数越高说明纯度越低,Gini系数越低说明纯度越高,每次选择Gini系数最小的特征作为节点,采用Gini系数衡量标准的决策树也称为CART(分类回归树)。
我们对比一下上面介绍的ID3、C4.5、CART。首先ID3只能用于离散型变量,这是由于ID3算法倾向于选择分支多的特征作为节点,这是该算法的一个缺陷,对于连续性变量而言,切割之后就会有较多的分支,所以ID3不能用于连续性变量。C4.5可以处理对连续变量进行切割的情况,因为C4.5算法可以通过分母中特征的熵进行惩罚。而对于CART,由于其构建时每次都会对特征进行二值划分,因此也可以很好地应用于连续性变量。
至此,我们就完成了关于决策树节点选择的讨论,但是决策树构建完成之后是不是就可以直接拿来使用了呢?事实上并非如此。我们需要对决策树进行剪枝瘦身,这样做的目的是减少一些判断,抑制“过拟合”现象的发生。
PySpark代码实现
1 from pyspark.sql import SparkSession 2 from pyspark.sql.functions import rand 3 4 spark = SparkSession.builder.appName('randomForest').getOrCreate() 5 # 读取数据文件 6 dfInfo = spark.read.csv('Social_Network_Ads.csv', inferSchema=True,header=True) 7 # 将类别变量性别转换成数值形式 8 from pyspark.ml.feature import StringIndexer 9 from pyspark.ml.feature import VectorAssembler 10 genderIndexer = StringIndexer(inputCol='Gender', outputCol='genderIndex').fit(dfInfo) 11 dfInfo = genderIndexer.transform(dfInfo) 12 13 # 将所有的输入列组装成新列,新列向量充当模型的输入特征 14 dfInfoAssembler = VectorAssembler(inputCols=['genderIndex','Age','EstimatedSalary'],outputCol='features') 15 dfInfo = dfInfoAssembler.transform(dfInfo) 16 17 dfInfo.select(['features', 'Purchased']).show(10,False) 18 dfInfoModel = dfInfo.select(['features', 'Purchased']) 19 # 划分数据集 20 training,test = dfInfoModel.randomSplit([0.75,0.25]) 21 # 构建和训练随机森林模型 22 from pyspark.ml.classification import RandomForestClassifier 23 rfModel = RandomForestClassifier(labelCol='Purchased').fit(training) 24 # 获取模型做出的预测 25 testRslt = rfModel.transform(test) 26 #testRslt.filter(testRslt['Purchased'] == 1).filter(testRslt['prediction'] == 1).\ 27 # select(['Purchased','prediction','probability']).show(100,False) 28 29 # 使用混淆矩阵评估模型性能[[TP,FN],[TN,FP]] 30 TP = testRslt.filter(testRslt['prediction'] == 1).filter(testRslt['Purchased'] == 1).count() 31 FN = testRslt.filter(testRslt['prediction'] == 0).filter(testRslt['Purchased'] == 1).count() 32 TN = testRslt.filter(testRslt['prediction'] == 0).filter(testRslt['Purchased'] == 0).count() 33 FP = testRslt.filter(testRslt['prediction'] == 1).filter(testRslt['Purchased'] == 0).count() 34 35 # 计算准确率 (TP+TN)/(TP+TN+FP+FN) 36 acc =(TP+TN)/(TP+TN+FP+FN) 37 # 计算召回率 TP/(TP+TN) 38 recall = TP/(TP+TN) 39 print('手动计算准确率 acc[{}]'.format(acc)) 40 41 # 评估预测的结果 42 from pyspark.ml.evaluation import MulticlassClassificationEvaluator 43 from pyspark.ml.evaluation import BinaryClassificationEvaluator 44 acc2 = MulticlassClassificationEvaluator(labelCol='Purchased', metricName='accuracy').evaluate(testRslt) 45 # AUC为roc曲线下的面积,AUC越接近与1.0说明检测方法的真实性越高 46 auc = BinaryClassificationEvaluator(labelCol='Purchased').evaluate(testRslt) 47 print('Spark评估模型准确率 acc[{}], auc[{}]'.format(acc2,auc))
代码运行结果
1 手动计算准确率 acc[0.9405940594059405] 2 Spark评估模型准确率 acc[0.9405940594059405], auc[0.9651268115942029]