mean Average Precision(mAP)
介绍mAP的概念之前,先来回顾一下几个概念:
TP: True Positive, 真正类,将正类预测成正类数。
TN: True Negtive, 真负类,将负类预测成负类数。
FP: False Positive, 假正类,将负类预测成正类。
FN: False Negtive, 假负类,将正类预测成负类。
| positive | negtive | |
|---|---|---|
| true | TP | FP |
| false | FN | TN |
根据以上内容,我们可以得到准确率(Accuracy)、精确率(precision)、召回率(recall)以及F1-score。
# 在所有样本中,分类正确的样本所占比例
Accuracy = (TP + TN) / (TP + TN + FP+ FN)
# 在预测的所有正样本中,预测正确的比例
precision = TP / (TP + FP)
# 在所有正样本中,预测为正样本的比例
recall = TP / (TP + FN)
# 精确率和召回率的一种权衡
F1 = 2 * precision * recall /(precision + recall)mAP是目标检测任务中通用的评估标准,那mAP是什么,为什么使用mAP呢。
在目标检测任务中,需要判断一个预测的边界框是否正确,我们会计算预测的边界框和真实框的iou,然后会设定一个阈值,如果iou > 阈值,那么就认为它预测正确。如果提高iou阈值,精确率会上升,召回率下降。iou减少阈值,召回率会上升,精确率下降。这样看来,只用一个阈值来评价网络模型肯定是不够的,那该如何在precision和recall之间实现一个trade off呢。
既然一个阈值不够,那么就取多个阈值,得到多个precision和recall。按照这样的方式可以得到如下的precision-recall曲线,也称PR曲线,PR曲线与坐标轴围成的面积即为AP。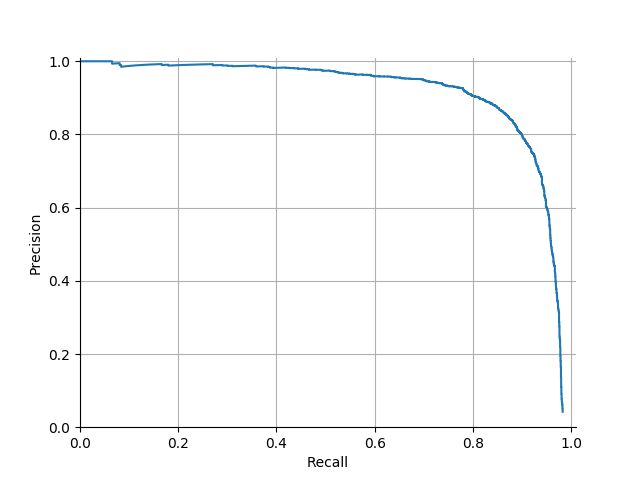
在Voc2010之前,只需选取Recall取[0, 0.1, 0.2, 0.3, 0.4, 0.5,0.6, 0.7, 0.8, 0.9, 1.0]共11个值,共对应11个点,然后计算PR曲线与坐标轴围成的面积作为AP。
在VOC2010及以后,需要针对每一个不同的Recall值(包括0和1),选取其大于等于这些Recall值时的Precision最大值,然后计算PR曲线下面积作为AP值。
每个类别可以得到一个PR曲线,对应一个AP。将所有类别的AP平均,即得到mAP。
这里计算的是插值平均AP,还有另外一种计算方式,它们之间的区别可以参考这里。
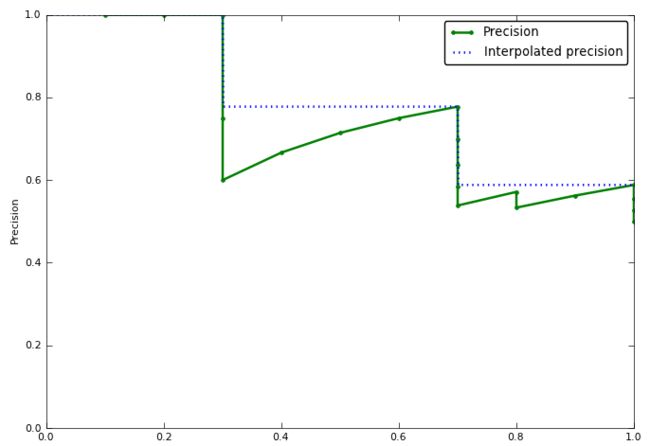
下图表示了原始的PR曲线(绿色)和插值后的PR曲线(蓝色虚线),直接计算原始PR曲线与坐标轴围成的面积较为困难(需计算积分),而计算蓝色虚线与坐标轴围成的面积则比较方便简单。插值法将PR曲线中上升的部分填平,保证了PR曲线是一条递减的曲线。
mAP计算代码如下:
1、首先计算每个类别的TP和FP,得到每个类别的精确率和召回率。
def calc_detection_voc_prec_rec(
pred_bboxes, pred_labels, pred_scores, gt_bboxes, gt_labels,
gt_difficults=None,
iou_thresh=0.5):
"""
Pascal Voc数据集的评估代码,用于计算精确率和召回率
Args:
pred_bboxes(list): 可迭代的预测框列表,其中的每一个元素都是一个数组.
pred_labels(list): 可迭代的预测标签列表.
pred_scores(list): 可迭代的预测概率列表.
gt_bboxes(list): 可迭代的真实框列表.
gt_labels(list): 可迭代的真实框标签列表.
gt_difficults(list): 可迭代的真实框预测难度列表,默认都为None,表示困难等级都为低.
iou_thresh (float): 如果预测框与对应的真实框的iou大于该阈值,则认为预测正确.
Returns:
rec(list):数组列表,rec[l]表示第l个类的召回率,如果第l个类不存在,则设为None.
pre(list): 数组列表,pre[l]表示第l个类的精确率,如果第l个类不存在,则设为None.
"""
# 将所有列表转为可迭代对象
pred_bboxes = iter(pred_bboxes)
pred_labels = iter(pred_labels)
pred_scores = iter(pred_scores)
gt_bboxes = iter(gt_bboxes)
gt_labels = iter(gt_labels)
if gt_difficults is None:
gt_difficults = itertools.repeat(None)
else:
gt_difficults = iter(gt_difficults)
# 每个类别等级为容易的真实框数目
n_pos = defaultdict(int)
#
score = defaultdict(list)
# 指示每个预测框是否匹配到真实框
match = defaultdict(list)
# pred_bbox, pred_label, pred_score, gt_bbox
# gt_label, gt_difficult 这6个列表的长度是相同的
# 每一次迭代,相当于一个batch
for pred_bbox, pred_label, pred_score, gt_bbox, gt_label, gt_difficult in \
six.moves.zip(
pred_bboxes, pred_labels, pred_scores,
gt_bboxes, gt_labels, gt_difficults):
if gt_difficult is None:
gt_difficult = np.zeros(gt_bbox.shape[0], dtype=bool)
# 分别处理每个类别
for l in np.unique(np.concatenate((pred_label, gt_label)).astype(int)):
# 取出属于第l个类别的预测框和预测得分
pred_mask_l = pred_label == l
pred_bbox_l = pred_bbox[pred_mask_l]
pred_score_l = pred_score[pred_mask_l]
# 将预测框按概率分值升序排序
order = pred_score_l.argsort()[::-1]
pred_bbox_l = pred_bbox_l[order]
pred_score_l = pred_score_l[order]
# 取出属于第l个类别的真实框
gt_mask_l = gt_label == l
gt_bbox_l = gt_bbox[gt_mask_l]
gt_difficult_l = gt_difficult[gt_mask_l]
# 按类别,统计非困难边框的数目,默认为全部
n_pos[l] += np.logical_not(gt_difficult_l).sum()
score[l].extend(pred_score_l)
# 如果没有预测框
if len(pred_bbox_l) == 0:
continue
# 如果真实框的数目为0, 则无匹配
if len(gt_bbox_l) == 0:
match[l].extend((0,) * pred_bbox_l.shape[0])
continue
pred_bbox_l[:, 2:] += 1
gt_bbox_l[:, 2:] += 1
# 计算预测框和真实框的iou
iou = bbox_iou(pred_bbox_l, gt_bbox_l)
# 得到与每一个预测框iou最大的真实框的索引
gt_index = iou.argmax(axis=1)
# iou小于阈值, 即说明没有与真实框对应的预测框, 则将索引设为-1
gt_index[iou.max(axis=1) < iou_thresh] = -1
del iou
# 指示真实框有没有被匹配上, 未匹配则标签为0,否则标签为1
# Note: 每个真实框只能匹配一个预测框一次
selec = np.zeros(gt_bbox_l.shape[0], dtype=bool)
for gt_idx in gt_index:
if gt_idx >= 0:
# 如果对应的真实框困难等级为高
if gt_difficult_l[gt_idx]:
match[l].append(-1)
else:
# 如果真实框为被匹配过,则进行匹配
if not selec[gt_idx]:
match[l].append(1)
else:
match[l].append(0)
# 设置索引gt_idx对应的预测框为已匹配
selec[gt_idx] = True
else:
match[l].append(0)
n_fg_class = max(n_pos.keys()) + 1
prec = [None] * n_fg_class
rec = [None] * n_fg_class
for l in n_pos.keys():
score_l = np.array(score[l])
match_l = np.array(match[l], dtype=np.int8)
# 按照预测类别概率降续排序
order = score_l.argsort()[::-1]
match_l = match_l[order]
tp = np.cumsum(match_l == 1)
fp = np.cumsum(match_l == 0)
# 如果fp + tp为0,则设置为prec[l]为nan
prec[l] = tp / (fp + tp)
# 如果n_pos[l]为0, 设置rec[l]为None.
if n_pos[l] > 0:
rec[l] = tp / n_pos[l]
return prec, rec2、根据pre和rec计算每个类别的AP。
def calc_detection_voc_ap(prec, rec, use_07_metric=False):
"""
Args:
prec: array列表.
rec: array列表.
Returns:
ap(array): 每个类别的平均精确率, shape -> (len(n_fg_class), )
"""
n_fg_class = len(prec)
ap = np.empty(n_fg_class)
for l in six.moves.range(n_fg_class):
if prec[l] is None or rec[l] is None:
ap[l] = np.nan
continue
if use_07_metric:
# 11 point metric
ap[l] = 0
for t in np.arange(0., 1.1, 0.1):
if np.sum(rec[l] >= t) == 0:
p = 0
else:
p = np.max(np.nan_to_num(prec[l])[rec[l] >= t])
ap[l] += p / 11
else:
# 插值
# 首尾插入0,保证最终的PR曲线递减
mpre = np.concatenate(([0], np.nan_to_num(prec[l]), [0]))
mrec = np.concatenate(([0], rec[l], [1]))
# np.maximum.accumulate 沿着指定轴, 从第二个元素起,将其与前一个元素进行比较, 取最大值
# 从后往前比较,取最大值,将PR曲线上升的部分填平
# 下面代码等同于
#for i in range(mpre.size - 1, 0, -1):
# mpre[i - 1] = np.maximum(mpre[i - 1], mpre[i])
mpre = np.maximum.accumulate(mpre[::-1])[::-1]
# 从第2个位置开始,获取与前一个值不相等的索引
i = np.where(mrec[1:] != mrec[:-1])[0]
# 计算面积
ap[l] = np.sum((mrec[i + 1] - mrec[i]) * mpre[i + 1])
return ap3、计算所有类别AP的平均。
Mean Intersection over Union(MIoU)
miou是语义分割任务中的模型评估标准, 每个类别的iou取平均之后得到miou。iou的计算如下图所示,iou = overlap / union。
miou计算代码如下:
- 计算混淆矩阵
def gen_matrix(gt_mask, pred_mask, class_num):
"""
gt_mask(ndarray): shape -> (height, width), 真实的分割图
pred_mask(ndarray):shape -> (height, width), 预测的分割结果
class_num: 类别数目,不包含背景
"""
mask = (gt_mask >= 0) & (gt_mask < n)
# bincount为计数函数,将数组从小到大排序后计数,默认从0到数组最大值计数。
count = np.bincount(n * gt_mask[mask].astype(int) \
+ pred_mask[mask], minlength=n ** 2)
# 混淆矩阵
cf_mtx = count.reshape(class_num, class_num)
return cf_mtx- 根据混淆矩阵计算所有类别的iou,最后平均得到mIou。
def mean_iou(cf_mtx):
"""
cf_mtx(ndarray): shape -> (class_num, class_num), 混淆矩阵
"""
#
mIou = np.diag(cf_mtx) / (np.sum(cf_mtx, axis=1) + \
np.sum(cf_mtx, axis=0) -np.diag(cf_mtx))
# 所有类别iou取平均
mIou = np.nanmean(mIou)
return mIouReference
https://github.com/chenyuntc/...
https://github.com/dmlc/gluon...