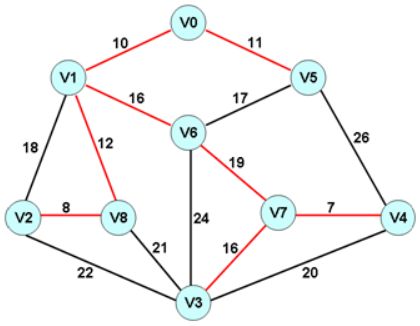
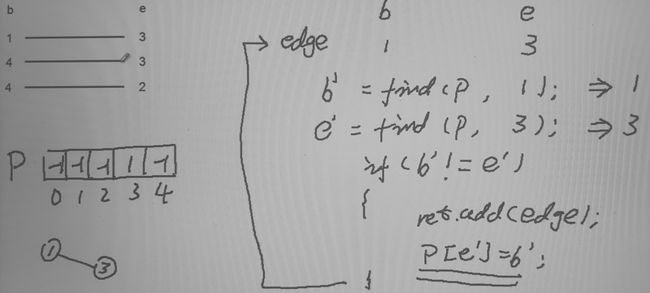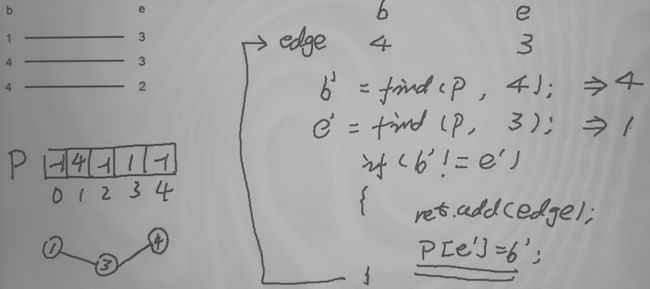最小生成树的特征
- 选取的边是图中权值较小的边
- 所有边连接后不构成回路
问题
既然最小生成树关心的是如何选择 n-1 条边,那么是否可以直接以边为核心进行算法设计?
简单尝试
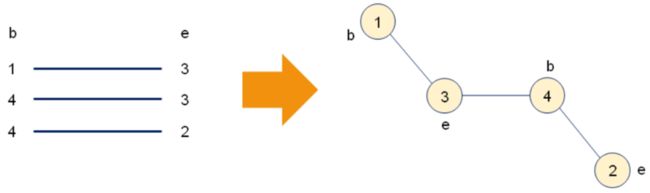
由 4 个顶点构成的图,选择 3 条权值最小的边
需要解决的问题
如何判断 新选择的边与已选择的边是否构成回路?
技巧:前驱标记数组
- 定义数组: Array
p(vCount()); 数组元素的定义:
- p[n] 表示顶点 n 在边的连接通路上的另一端顶点
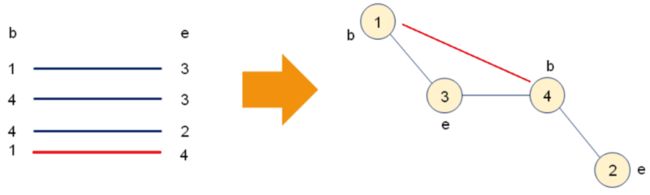
示例分析:使用标记数组选择边
回路边时:
最小生成树算法的核心步骤(Kruskal)
- 定义前驱标记数组: Array
p(vCount()) - 获取当前图中的所有边,并保存于 edges 数组中
- 对数组 edges 按照权值进行排序
- 利用 p 数组在 edges 数组选择前 n-1 不构成回路的边
Kruskal 算法流程
关键的 find 查找函数
int find(Array &p, int v)
{
while (p[v] != -1)
{
v = p[v];
}
return v;
} 编程实验:最小生成树算法
文件:Graph.h
#ifndef GRAPH_H
#define GRAPH_H
#include "Object.h"
#include "SharedPointer.h"
#include "DynamicArray.h"
#include "LinkQueue.h"
#include "LinkStack.h"
#include "Sort.h"
namespace DTLib
{
template
struct Edge : public Object
{
int b;
int e;
E data;
Edge(int i=-1, int j=-1) : b(i), e(j)
{
}
Edge(int i, int j, const E &value) : b(i), e(j), data(value)
{
}
bool operator == (const Edge &obj)
{
return (b == obj.b) && (e == obj.e);
}
bool operator != (const Edge &obj)
{
return !(*this == obj);
}
bool operator < (const Edge &obj)
{
return (data < obj.data);
}
bool operator > (const Edge &obj)
{
return (data > obj.data);
}
};
template
class Graph : public Object
{
public:
virtual V getVertex(int i) const = 0;
virtual bool getVertex(int i, V &value) const = 0;
virtual bool setVertex(int i, const V &value) = 0;
virtual SharedPointer> getAdjacent(int i) const = 0;
virtual bool isAdjacent(int i, int j) const = 0;
virtual E getEdge(int i, int j) const = 0;
virtual bool getEdge(int i, int j, E &value) const = 0;
virtual bool setEdge(int i, int j, const E &value) = 0;
virtual bool removeEdge(int i, int j) = 0;
virtual int vCount() const = 0;
virtual int eCount() = 0;
virtual int OD(int i) = 0;
virtual int ID(int i) = 0;
virtual int TD(int i)
{
return OD(i) + ID(i);
}
bool asUndirected()
{
bool ret = true;
for (int i=0; i> BFS(int i)
{
DynamicArray *ret = nullptr;
if ((0 <= i) && (i < vCount()))
{
LinkQueue q;
LinkQueue r;
DynamicArray visited(vCount());
for (int j=0; j 0)
{
int v = q.front();
q.remove();
if (!visited[v])
{
SharedPointer> aj = getAdjacent(v);
for (int j=0; jlength(); ++j)
{
q.add((*aj)[j]);
}
r.add(v);
visited[v] = true;
}
}
ret = toArray(r);
}
else
{
THROW_EXCEPTION(InvalidParameterExcetion, "Parameter i is invalid ...");
}
return ret;
}
#ifdef DFS_R
SharedPointer> DFS(int i) // 递归版深度优先遍历
{
DynamicArray *ret = nullptr;
if ((0 <= i) && (i < vCount()))
{
LinkQueue r;
DynamicArray visited(vCount());
for (int j=0; j> DFS(int i)
{
DynamicArray *ret = nullptr;
if ((0 <= i) && (i < vCount()))
{
LinkStack s;
LinkQueue r;
DynamicArray visited(vCount());
for (int j=0; j 0)
{
int v = s.top();
s.pop();
if (!visited[v])
{
SharedPointer> aj = getAdjacent(v);
for (int j=aj->length()-1; j>=0; --j)
{
s.push((*aj)[j]);
}
r.add(v);
visited[v] = true;
}
}
ret = toArray(r);
}
else
{
THROW_EXCEPTION(InvalidParameterExcetion, "Parameter i is invalid ...");
}
return ret;
}
#endif
SharedPointer>> prim(const E &LIMIT, const bool MINIMUM = true)
{
LinkQueue> ret;
if (asUndirected())
{
DynamicArray adjVex(vCount());
DynamicArray mark(vCount());
DynamicArray cost(vCount());
SharedPointer> aj = nullptr;
bool end = false;
int v = 0;
for (int i=0; ilength(); ++i)
{
cost[(*aj)[i]] = getEdge(v, (*aj)[i]);
adjVex[(*aj)[i]] = v;
}
for (int i=0; i cost[j]) : (m < cost[j])))
{
m = cost[j];
k = j;
}
}
end = (k == -1);
if (!end)
{
ret.add(Edge(adjVex[k],k, getEdge(adjVex[k],k)));
mark[k] = true;
aj = getAdjacent(k);
for (int j=0; jlength(); ++j)
{
if (!mark[(*aj)[j]] && (MINIMUM ? (getEdge(k, (*aj)[j]) < cost[(*aj)[j]]) : (getEdge(k, (*aj)[j]) > cost[(*aj)[j]])))
{
cost[(*aj)[j]] = getEdge(k, (*aj)[j]);
adjVex[(*aj)[j]] = k;
}
}
}
}
}
else
{
THROW_EXCEPTION(InvalidOpertionExcetion, "Prim operator is for undirected grap only ...");
}
if (ret.length() != (vCount() - 1))
{
THROW_EXCEPTION(InvalidOpertionExcetion, "No enough edge for prim operation ...");
}
return toArray(ret);
}
SharedPointer>> Kruskal( const bool MINIMUM = true)
{
LinkQueue> ret;
DynamicArray p(vCount());
SharedPointer>> edges = getUndirectedEdges();
for (int i=0; ilength()) && (ret.length() < (vCount()-1)); ++i)
{
int b = find(p, (*edges)[i].b);
int e = find(p, (*edges)[i].e);
if (b != e)
{
p[e] = b;
ret.add((*edges)[i]);
}
}
if (ret.length() != vCount() - 1)
{
THROW_EXCEPTION(InvalidOpertionExcetion, "No enough edges for Kruskal operation ...");
}
return toArray(ret);
}
protected:
template
DynamicArray* toArray(LinkQueue &queue)
{
DynamicArray *ret = new DynamicArray(queue.length());
if (ret != nullptr)
{
for (int i=0; ilength(); ++i, queue.remove())
{
ret->set(i, queue.front());
}
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create ret obj ...");
}
return ret;
}
#ifdef DFS_R
void DFP(int i, DynamicArray &visited, LinkQueue& queue)
{
if (!visited[i])
{
queue.add(i);
visited[i] = true;
SharedPointer> aj = getAdjacent(i);
for (int j=0; jlength(); ++j)
{
DFP((*aj)[j], visited, queue);
}
}
}
#endif
int find(Array &p, int v)
{
while (p[v] != -1)
{
v = p[v];
}
return v;
}
SharedPointer>> getUndirectedEdges()
{
DynamicArray> *ret = nullptr;
if (asUndirected())
{
LinkQueue> queue;
for (int i=0; i(i, j, getEdge(i, j)));
}
}
}
ret = toArray(queue);
}
else
{
THROW_EXCEPTION(InvalidOpertionExcetion, "This function is for undirected graph only ...");
}
return ret;
}
};
}
#endif // GRAPH_H 文件:main.cpp
#include
#include "MatrixGraph.h"
#include "ListGraph.h"
using namespace std;
using namespace DTLib;
template< typename V, typename E >
Graph& GraphEasy()
{
static MatrixGraph<4, V, E> g;
g.setEdge(0, 1, 1);
g.setEdge(1, 0, 1);
g.setEdge(0, 2, 3);
g.setEdge(2, 0, 3);
g.setEdge(1, 2, 1);
g.setEdge(2, 1, 1);
g.setEdge(1, 3, 4);
g.setEdge(3, 1, 4);
g.setEdge(2, 3, 1);
g.setEdge(3, 2, 1);
return g;
}
template< typename V, typename E >
Graph& GraphComplex()
{
static ListGraph g(9);
g.setEdge(0, 1, 10);
g.setEdge(1, 0, 10);
g.setEdge(0, 5, 11);
g.setEdge(5, 0, 11);
g.setEdge(1, 2, 18);
g.setEdge(2, 1, 18);
g.setEdge(1, 8, 12);
g.setEdge(8, 1, 12);
g.setEdge(1, 6, 16);
g.setEdge(6, 1, 16);
g.setEdge(2, 3, 22);
g.setEdge(3, 2, 22);
g.setEdge(2, 8, 8);
g.setEdge(8, 2, 8);
g.setEdge(3, 8, 21);
g.setEdge(8, 3, 21);
g.setEdge(3, 6, 24);
g.setEdge(6, 3, 24);
g.setEdge(3, 7, 16);
g.setEdge(7, 3, 16);
g.setEdge(3, 4, 20);
g.setEdge(4, 3, 20);
g.setEdge(4, 5, 26);
g.setEdge(5, 4, 26);
g.setEdge(4, 7, 7);
g.setEdge(7, 4, 7);
g.setEdge(5, 6, 17);
g.setEdge(6, 5, 17);
g.setEdge(6, 7, 19);
g.setEdge(7, 6, 19);
return g;
}
void func1()
{
cout << "func1: ---------------------" << endl;
Graph& g = GraphEasy();
SharedPointer< Array< Edge > > sa = g.Kruskal();
int w = 0;
for(int i=0; ilength(); i++)
{
w += (*sa)[i].data;
cout << (*sa)[i].b << " " << (*sa)[i].e << " " << (*sa)[i].data << endl;
}
cout << "Weight: " << w << endl;
}
void func2()
{
cout << "func2: ---------------------" << endl;
Graph& g = GraphComplex();
SharedPointer< Array< Edge > > sa = g.Kruskal();
int w = 0;
for(int i=0; ilength(); i++)
{
w += (*sa)[i].data;
cout << (*sa)[i].b << " " << (*sa)[i].e << " " << (*sa)[i].data << endl;
}
cout << "Weight: " << w << endl;
}
void func3()
{
cout << "func3: ---------------------" << endl;
Graph& g = GraphComplex();
SharedPointer< Array< Edge > > sa = g.Kruskal(false);
int w = 0;
for(int i=0; ilength(); i++)
{
w += (*sa)[i].data;
cout << (*sa)[i].b << " " << (*sa)[i].e << " " << (*sa)[i].data << endl;
}
cout << "Weight: " << w << endl;
}
int main()
{
func1();
func2();
func3();
return 0;
} 输出:
func1: ---------------------
0 1 1
1 2 1
2 3 1
Weight: 3
func2: ---------------------
4 7 7
2 8 8
1 0 10
0 5 11
1 8 12
1 6 16
3 7 16
7 6 19
Weight: 99
func3: ---------------------
5 4 26
3 6 24
2 3 22
3 8 21
3 4 20
7 6 19
1 2 18
0 5 11
Weight: 161小结
- Prim 算法以顶点为核心寻找最小生成树,不够直接
- Kruskal 算法以边为核心寻找最小生成树,直观简单
- Kruskal 算法中的关键是前驱标记数组的使用
- 前驱标记数组用于判断新选择的边是否会造成回路
以上内容整理于狄泰软件学院系列课程,请大家保护原创!