Q:
一些恶魔抓住了公主(P)并将她关在了地下城的右下角。地下城是由 M x N 个房间组成的二维网格。我们英勇的骑士(K)最初被安置在左上角的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快到达公主,骑士决定每次只向右或向下移动一步。
编写一个函数来计算确保骑士能够拯救到公主所需的最低初始健康点数。
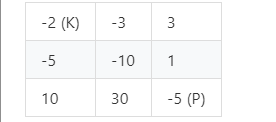
例如,考虑到如下布局的地下城,如果骑士遵循最佳路径 右 -> 右 -> 下 -> 下,则骑士的初始健康点数至少为 7。
-2 (K) -3 3
-5 -10 1
10 30 -5 §
说明:
骑士的健康点数没有上限。
任何房间都可能对骑士的健康点数造成威胁,也可能增加骑士的健康点数,包括骑士进入的左上角房间以及公主被监禁的右下角房间。
A:
又自己想了一下为什么不能用正向DP。原因在于后效性这点不符合。假设我们正向DP,即从左上角向右下角前进,dp[i][j]表示从左上角到该位置最小需要的健康值。
例子:
我们假设考虑dp[2][0],从上面-2,-5过来,最少需要8滴血,那么dp[i][j]就填8吗,还是填1(毕竟这个房间可以加10滴血,只要来的时候不死就行了)?这里就是问题所在。对于某个状态(即某个确切的i,j坐标),它对于之后的路径是有影响的。因为除了考虑安全到达当前状态之外,还需要考虑从当前状态不死安全抵达公主。(即怎么到达当前状态会对之后的状态造成影响,这就不符合动态规划的无后效性了)
顺便粘贴一个知乎的回答:https://www.zhihu.com/question/43361359/answer/129799087
从不同的路径走到一个共同状态,而后续的状态变迁都是一样的,和之前采用何种路径到这个状态没有关系,即前面的各种决策结果由这个状态表示,在考虑后半段的决策方面没有任何区别
那么为什么逆序就可以?因为动态规划是要求无后效性,而不要求无前效性(虽然没有这个名词)。我们逆序的dp[i][j]表示从当前位置开始,安全抵达公主所需的最少健康值,不考虑怎么到达i,j,而是只关心从i,j开始如何抵达公主。可以看到,我们对于状态的定义不包含该状态之前的事件,也就不会有什么当前状态之前的事件对当前状态之后 造成影响!
这是我的想法,如果有懂这方面的大佬麻烦评论指点一哈
代码:
1 class Solution: 2 def calculateMinimumHP(self, dungeon ) -> int: 3 m,n=len(dungeon),0 4 if not m: 5 return 0 6 n=len(dungeon[0]) 7 dp=[[1 for i in range(n)] for j in range(m)] #m行n列 8 #dp[i][j]为从当前房间出发能不死抵达公主所需的最低健康点数 9 dp[-1][-1]=max(1,1-dungeon[-1][-1]) 10 for i in range(m-1,-1,-1): 11 for j in range(n-1,-1,-1): 12 if i==m-1 and j==n-1: 13 continue 14 x1,x2=float('inf'),float('inf') 15 if i+1<m: 16 x1=max(1,dp[i+1][j]-dungeon[i][j]) 17 if j+1<n: 18 x2=max(1,dp[i][j+1]-dungeon[i][j]) 19 dp[i][j]=min(x1,x2) 20 # for x in dp: 21 # print(x) 22 return dp[0][0]
把最后一行、最后一列单独判断一下,别人的代码:
1 class Solution: 2 def calculateMinimumHP(self, dungeon: List[List[int]]) -> int: 3 dp = [[0 for i in range(len(dungeon[0]))] for j in range(len(dungeon))] 4 m = len(dungeon) 5 n = len(dungeon[0]) 6 dp[-1][-1] = max(1, 1 - dungeon[-1][-1]) 7 for i in range(m-2,-1,-1): 8 dp[i][-1] = max(1,dp[i+1][-1]-dungeon[i][-1]) 9 for j in range(n-2,-1,-1): 10 dp[-1][j] = max(1, dp[-1][j+1] - dungeon[-1][j]) 11 for i in range(m-2,-1,-1): 12 for j in range(n-2,-1,-1): 13 dp[i][j] = max(1,min(dp[i+1][j],dp[i][j+1])-dungeon[i][j]) 14 return dp[0][0]