Percetron Learning Algorithm——感知学习算法。

算法原理

PLA用于解决的是对于二维或者高维的线性可分问题的分类，最终将问题分为两类——是或者不是。针对给定的feature vector给出Yes 或者 No的回答。值得注意的是PLA一定是针对线性可分的问题，即可以找到一条线，或者超平面去分开是和不是的两堆数据，如果不是线性可分。可以通过Pocket改正算法，类似贪心的法则找到一个最适合的权值。
找到一个合适的权值之后，使用该权值对测试集进行二分类。

抽象模型

AI基于Matlab Percetron Learning Algorithm——感知学习算法_第1张图片

image.png

权重向量 wi, 1<=i<=d;
阈值，下面设为0
做一点小小的变形使得式子更加紧凑

AI基于Matlab Percetron Learning Algorithm——感知学习算法_第2张图片

image.png

PLA算法"知错能改"，其循环是不断遍历feature vector，找到错误的点，即y和当前w*x不符合，然后校正w，那么为什么要这样校正呢？因为这样可以保证Wt越来越靠近perfect直线w

评测指标

AI基于Matlab Percetron Learning Algorithm——感知学习算法_第3张图片

image.png

对于二元分类有这样的指标，Accuracy(准确率)\Precision(精确率)Recall(召回率)F1(F值)

AI基于Matlab Percetron Learning Algorithm——感知学习算法_第4张图片

image.png

TP：本来为+1，预测为+1

FN：本来为+1，预测为-1

TN：本来为-1，预测为-1

FP：本来为-1，预测为+1

T：True   F：False
N：negative   P：positive

ROC指标

   True Positive Rate ( TPR )  = TP / [ TP + FN] ，TPR代表能将正例分对的概率
   
False Positive Rate( FPR ) = FP / [ FP + TN] ，FPR代表将负例错分为正例的概率

在ROC 空间中，每个点的横坐标是FPR，纵坐标是TPR，这也就描绘了分类器在TP（真正的正例）和FP（错误的正例）间的trade-off。ROC的主要分析工具是一个画在ROC空间的曲线——ROC curve。我们知道，对于二值分类问题，实例的值往往是连续值，我们通过设定一个阈值，将实例分类到正类或者负类（比如大于阈值划分为正类）。因此我们可以变化阈值，根据不同的阈值进行分类，根据分类结果计算得到ROC空间中相应的点，连接这些点就形成ROC curve。ROC curve经过（0,0）（1,1），实际上(0, 0)和(1, 1)连线形成的ROC curve实际上代表的是一个随机分类器。一般情况下，这个曲线都应该处于(0, 0)和(1, 1)连线的上方。

算法伪代码

原始PLA伪代码

AI基于Matlab Percetron Learning Algorithm——感知学习算法_第5张图片

image.png

PLA的优缺点

1.首先，PLA的算法是局限在线性可分的训练集上的，然而我们拿到一个训练集，并不知道其到底是不是线性可分，如果不是，PLA的算法程序将无限循环下去，这样做是不可行的。

2.即使训练集是线性可分，我们也不知道PLA什么时候才能找到一个合适的解，如果要循环很多次才能找到，这对于实际使用是开销很大的。

Pocket-PLA伪代码

AI基于Matlab Percetron Learning Algorithm——感知学习算法_第6张图片

image.png

Pocket-PLA需要找到一条分界线去分离两个数据集，使得错误率最低

然而要准确找到一条错误率最低的，被证明出是一个NP问题，不能准确地找到。那么Pocket算法的思路就是，类似贪心，如果找到一个更好(错误率低)的w，那么就去更新，如果找一个错误率更高的，那么就不去更新的，重新找。每次找一个随机的wt。对于所有数据都采用w(t+1) = w(t) + yn*xn;修正一次。最后如果这个wt要比记录的最好值w‘犯的错误少，就更新最好值。

Pocket优缺点

1.wt是随机的，可能算了很多次都没有找出一个更好的。

2.假设数据一开始就是线性可分，那么这个算法找出来的未必是最好解，且时间花费也可能比较大。

小数据集验证模型

小数据集说明：因为实验数据给出的分类不平衡，所以我从网络上找到可一个开源的数据集，权值的维度是2，方便可视化，且这个数据集+1和-1的分类比例比较平均，并且是非线性可分的。

set	权值维度	数量	y=+1	y=-1
train	2	200	100	100
validation	2	50	25	25

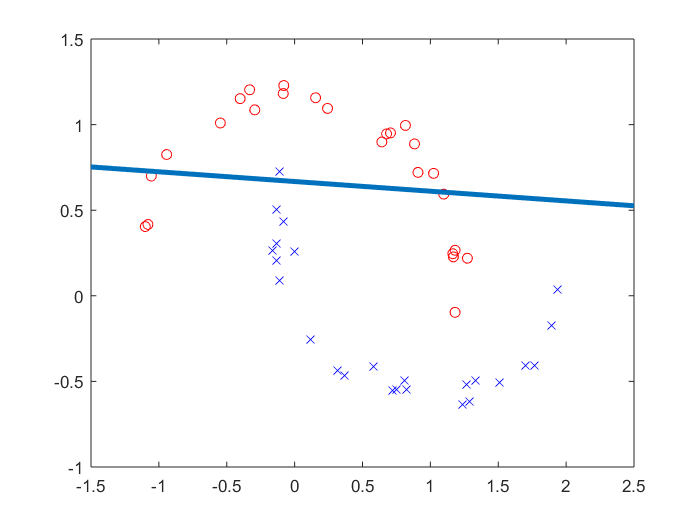
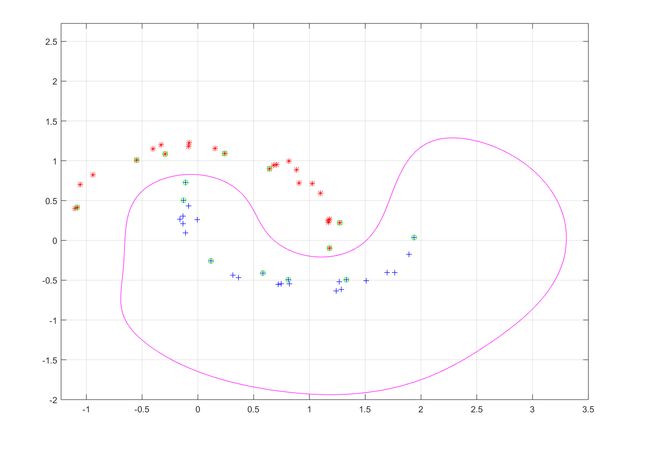
小训练集数据分布如下图

观察可得我确实没找出一条线能够划分开两个不同类别。红色o表示+1，蓝色x表示-1

AI基于Matlab Percetron Learning Algorithm——感知学习算法_第7张图片

小训练集数据分布.png

下面展示应用我的模型的划分过程

迭代过程1：迭代次数过少，分类效果很差

AI基于Matlab Percetron Learning Algorithm——感知学习算法_第8张图片

100小训练集划分.png

迭代过程2：当迭代次数逐渐增多，直线慢慢像最优权值靠拢（体现PLA学习的过程）

AI基于Matlab Percetron Learning Algorithm——感知学习算法_第9张图片

115小训练集划分.png

迭代过程3：由于测试集非线性可分，当权值很久没有改变的时候，退出迭代的循环

AI基于Matlab Percetron Learning Algorithm——感知学习算法_第10张图片

小训练集划分.png

应用权值（直线）对验证集划分

使用通过Train得到的直线（最优权值）进行测试分类器的效果

AI基于Matlab Percetron Learning Algorithm——感知学习算法_第11张图片

验证集集划分.png

结果

指标

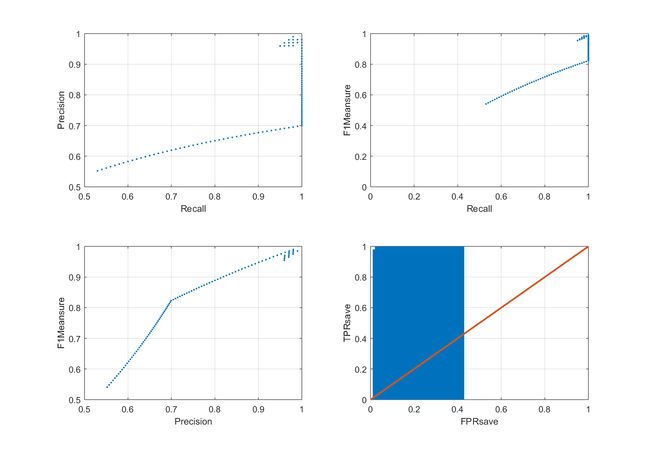
左上：Precision-Recall

右上：F1-Recall

左下：F1-Precision

右下：TPR-FPR，显示在y=x这条线上方的面积较大，该分类器效果较好

AI基于Matlab Percetron Learning Algorithm——感知学习算法_第12张图片

指标.png

关键代码和注释

Limit.m——限制迭代次数PLA与Pocket结合

clear A
clear P
clear R
clear TPRsave
clear FPRsave
clear F1Meansure

% augmented matrix 增广矩阵
xn=augmentedmatrix(train);
size_label=size(label);
sizeL=size_label(1);
size_xn=size(xn);

% 随机预测标签
Rand=randi([0,1],size_label(1),size_label(2));
Rand(Rand==0)=-1;
predictlabel=Rand;
Acc=Accuracy(label,predictlabel,sizeL);

tim=1;% 总迭代次数
count=1;% PLA-Pocket算法 权值何时放入口袋
iterator=1;% 原始PLA 算法迭代次数

% 用于画图
A=[];% 记录正确率
P=[];% 记录精确率
R=[];% 记录召回率
TPRsave=[];% 记录TPR
FPRsave=[];% 记录FPR
F1Meansure=[];% 记录F1

maxAcc=0;
maxF1=0;

% 初始化权值向量
maxW=ones(size_xn(1),1);
new_w=ones(size_xn(1),1);
w=ones(size_xn(1),1);

while(tim<=10000)
    if maxAcc==1
        break;
    end
    
    % 更新W
    predictlabel(iterator)=Sign((w')*xn(:,iterator));
    if predictlabel(iterator)~=label(iterator)
        new_w=w+label(iterator)*xn(:,iterator);
        w=new_w;
    end

    if count==4000
        count=0;
        tim=tim+1;
        Acc=Accuracy(label,predictlabel,sizeL);
        Pre=Precision(label,predictlabel,sizeL);
        Rec=Recall(label,predictlabel,sizeL);
        TPR=TruePositiveRate(label,predictlabel,sizeL);
        FPR=FalsePositiveRate(label,predictlabel,sizeL);
        F=F1(Pre,Rec,1);
        A=[A,Acc];
        P=[P,Pre];
        R=[R,Rec];
        TPRsave=[TPRsave,TPR];
        FPRsave=[FPRsave,FPR];
        F1Meansure=[F1Meansure,F];
        
        % pocket 记录最好的权值向量
        if F>maxF1
            maxF1=F;
            maxW=new_w;
        end
    end
    if iterator==size_xn(2)
        iterator=0;
    end
    iterator=iterator+1;
    count=count+1;
    
end

Pocket.m ——随机口袋算法

% augmented matrix
xn=augmentedmatrix(train);
% initial w
w=10000*rand(size_xn(1),1);
tim=1;


while(tim<=1000)
    w=10000*rand(size_xn(1),1);% 产生随机权值向量W
    
    for iterator=1:size_xn(2)% 使用验证集对W更新一次
        predictlabel(iterator)=Sign((w')*xn(:,iterator));
        if predictlabel(iterator)~=label(iterator)
            new_w=w+label(iterator)*xn(:,iterator);
            w=new_w;
        end
    end
    
    % 计算各个指标
    Acc=Accuracy(label,predictlabel,sizeL);
    Pre=Precision(label,predictlabel,sizeL);
    Rec=Recall(label,predictlabel,sizeL);
    TPR=TruePositiveRate(label,predictlabel,sizeL);
    FPR=FalsePositiveRate(label,predictlabel,sizeL);
    F=F1(Pre,Rec,5);
    A=[A,Acc];
    P=[P,Pre];
    R=[R,Rec];
    TPRsave=[TPRsave,TPR];
    FPRsave=[FPRsave,FPR];
    F1Meansure=[F1Meansure,F];
    % 进入口袋Pocket的条件
    if F>maxF1
            maxF1=F;
            maxW=new_w;
    end
    tim=tim+1;
end

计算各类指标

% 计算准确率
function Acc=Accuracy(label,predictlabel,sizeL)
    error=label-predictlabel;
    TP=sizeL-(sum(abs(error))/2);
    Acc=TP/sizeL;
end

% 计算精确率
function Pre=Precision(label,predictlabel,sizeL)
    TP=0;
    FP=0;
    for i=1:sizeL
        if label(i)==1 && predictlabel(i)==1
            TP=TP+1;
        elseif label(i)==-1 && predictlabel(i)==1
            FP=FP+1;
        end
    end
    Pre=TP/(TP+FP);
end

% 计算召回率
function Rec=Recall(label,predictlabel,sizeL)
    TP=0;
    FN=0;
    for i=1:sizeL
        if label(i)==1 && predictlabel(i)==1
            TP=TP+1;
        elseif label(i)==1 && predictlabel(i)==-1
            FN=FN+1;
        end
    end
    Rec=TP/(TP+FN);
end

% 计算F值（加权版）
function F=F1(Pre,Rec,a)
    fenzi=a*a+1;
    fenmu=a*a;
    F=(fenzi*(Pre*Rec))/(fenmu*(Pre+Rec));
end

% 符号函数
function yout=Sign(yin)
    if yin>0
        yout=1;
    elseif yin<0
        yout=-1;
    end
end

%ROC横纵坐标计算
function TPR=TruePositiveRate(label,predictlabel,sizeL)
    TP=0;
    FN=0;
    for i=1:sizeL
        if label(i)==1 && predictlabel(i)==1
            TP=TP+1;
        elseif label(i)==1 && predictlabel(i)==-1
            FN=FN+1;
        end
    end
    TPR=TP/(TP+FN);
end

function FPR=FalsePositiveRate(label,predictlabel,sizeL)
    FP=0;
    TN=0;
    for i=1:sizeL
        if label(i)==-1 && predictlabel(i)==1
            FP=FP+1;
        elseif label(i)==-1 && predictlabel(i)==-1
            TN=TN+1;
        end
    end
    FPR=FP/(FP+TN);
end

实验结果和评测指标

通过train训练出的权值向量VectorW，作用于validation进行二分类
列表放结果

评测指标图

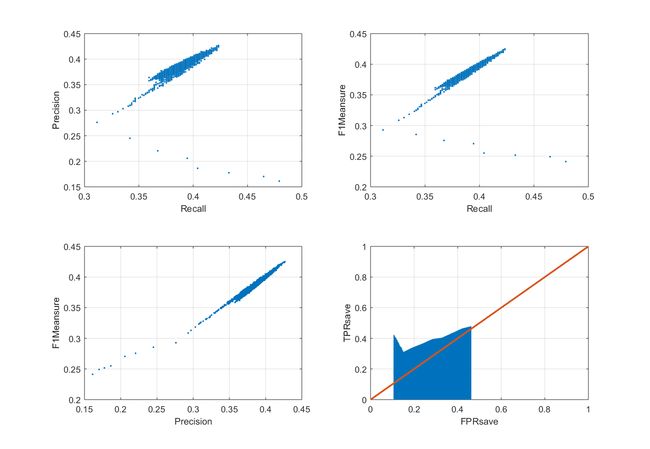
左上：Precision-Recall

右上：F1-Recall

左下：F1-Precision

右下：TPR-FPR

评测说明

准确率和召回率是互相影响的，理想情况下肯定是做到两者都高，但是一般情况下准确率高、召回率就低，召回率低、准确率高，当然如果两者都低，那是什么地方出问题了

Precision-Recall曲线与坐标轴之间的面积应当越大。
最理想的系统，其包含的面积应当是1，而所有系统的包含的面积都应当大于0。

TPR-FPR 在ROC 空间中，每个点的横坐标是FPR，纵坐标是TPR，这也就描绘了分类器在TP（真正的正例）和FP（错误的正例）间的trade-off。ROC的主要分析工具是一个画在ROC空间的曲线——ROC curve。我们知道，对于二值分类问题，实例的值往往是连续值，我们通过设定一个阈值，将实例分类到正类或者负类（比如大于阈值划分为正类）。因此我们可以变化阈值，根据不同的阈值进行分类，根据分类结果计算得到ROC空间中相应的点，连接这些点就形成ROC curve。ROC curve经过（0,0）（1,1），实际上(0, 0)和(1, 1)连线形成的ROC curve实际上代表的是一个随机分类器。一般情况下，这个曲线都应该处于(0, 0)和(1, 1)连线的上方。用ROC curve来表示分类器的performance很直观好用。可是，人们总是希望能有一个数值来标志分类器的好坏。
于是Area Under roc Curve(AUC)就出现了。顾名思义，AUC的值就是处于ROC curve下方的那部分面积的大小。通常，AUC的值介于0.5到1.0之间，较大的AUC代表了较好的Performance。

设计PLA二分类模型结果分析

计算的F1值都是在alpha=1的情况下

迭代次数为500次，pocket以F1的阈值为准

maxWeight on validation 

Acc = 0.815000000000000

Pre = 0.373737373737374

Rec = 0.231250000000000

F = 0.285714285714286

分析：迭代次数过少，分类器效果不明显。

右下图TPR-FPR 蓝色为分类器曲线，橙色为y=x，曲线都在y=x下方，说明分类器效果不好

AI基于Matlab Percetron Learning Algorithm——感知学习算法_第13张图片

tim=1000，count=1.png

迭代次数为1000次，pocket以F1的阈值为准

maxWeight on validation 

Acc = 0.831000000000000


Pre = 0.445783132530120


Rec = 0.231250000000000


F = 0.304526748971193

分析：随着迭代次数的增大，pocket里收入了效果较好的权值

左上：Precision-Recall 曲线下凹，说明精确率和召回率，鱼与熊掌不可兼得，曲线越上凸，分类器效果越好。

右下：TPR-FPR 蓝色为分类器曲线，橙色为y=x，曲线都在y=x上方了，与上一张图相比分类器性能变好了一些

AI基于Matlab Percetron Learning Algorithm——感知学习算法_第14张图片

tim=10000，count=1.png

迭代次数为10000次，pocket以F1的阈值为准

maxWeight on validation 

Acc = 0.822000000000000


Pre = 0.436619718309859


Rec = 0.387500000000000


F = 0.410596026490066

分析：随着迭代次数的增大，pocket里收入了效果更好的权值

右下：TPR-FPR 蓝色为分类器曲线，橙色为y=x，曲线都在y=x上方了，与上一张图相比，橙色线上方面积大一些

AI基于Matlab Percetron Learning Algorithm——感知学习算法_第15张图片

tim=10000，count=1000.png

迭代次数为100000次，pocket以F1的阈值为准

maxWeight on validation 

Acc = 0.796000000000000


Pre =  0.409090909090909


Rec = 0.618750000000000


F =

   0.492537313432836

分析：随着迭代次数的增大，pocket里收入了效果更好的权值

之后很多次的迭代，都是为了pocket里收入的权值能使召回率Rec上升，照顾到更多的少数民族+1

AI基于Matlab Percetron Learning Algorithm——感知学习算法_第16张图片

tim=1000，count=1000.png

Pocket-PLA

当alpha为1的时候

validation

Acc = 0.796000000000000


Pre = 0.402654867256637


Rec = 0.568750000000000


F = 0.471502590673575

AI基于Matlab Percetron Learning Algorithm——感知学习算法_第17张图片

pocketPLA1指标.png

当alpha从0.1~10
不断调高的过程中recall也会增加
最后我取定alpha=5时，也是比较随缘的

此时验证集结果为：

Acc = 0.795000000000000


Pre = 0.403433476394850


Rec = 0.587500000000000


F = 0.241577608142494

纯Pocket-PLA，运行次数的增加并没有增加Recall召回率，而是取决于每次生成的初始权值向量W是否能够训练出较好的模型

AI基于Matlab Percetron Learning Algorithm——感知学习算法_第18张图片

image.png

产生test测试集结果注明：

Model：结合了规定迭代次数的PLA算法与随机口袋算法

iterator：100000

alpha：5

validation result
Acc =  0.795000000000000
Pre = 0.403433476394850
Rec = 0.587500000000000
F = 0.241577608142494

优化点

1、结合了规定迭代次数的PLA算法与随机口袋算法
规定迭代次数PLA算法是经过若干次不断的轮询调整之后，从初始化权值W=1，得到一个权值W-PLA，缺点是循环很多次才能找到，这对于实际使用是开销很大，也不知道什么时候才能找到。
随机口袋算法是使用随机数产生一个权值，利用这个初始随机的权值，经过所有样本更新一次，得到一个权值W-Pocket，判断该权值是否使错误率更小，如果错误率更小则更新权值。缺点是W-Pocket的初始化是随机的，不确定性大，可能算了很多次都没有找出一个更好的。

这两者可以相结合，首先使用“规定迭代次数”的PLA算法得到一个权值W-PLA，然后把这个权值作为口袋算法的初始权值，经过训练集的更新，记录结果。重复多次，再使用W-Pocket的权值作为“规定迭代次数”的PLA的初始权值。这样可以保证设置的迭代次数不用太多，耗时不长，口袋算法的不确定性减小。

使用改优化后召回率明显上升。

2.使用了一般意义下的F1作为指标
用于优化口袋算法

image.png

为什么选择用这个指标呢？
在本次实验中，我认为召回率Recall的重要性很大，因为训练集数据分类不平衡，y=-1的有百分之八十多，如果只根据正确率Accuracy来作为评测指标，那这个算法变得非常简单，把所有的分类都判断为-1，那正确率就很高了，完爆了我写的其他PLA分类器辛辛苦苦算出来的权值。这样的分类在测试集中表现有可能会出现很大的偏差，万一测试集里+1居多呢。

本次实验中召回率是
Recall=（【预测为+1且实际也是+1】）/（【预测为+1且实际为+1】加上【预测为-1但是实际是+1】）
表征的特点是，我的分类器，对于实际是+1的，到底预测对了多少。训练集-1居多，那更应该关注一下+1的标签们。

当alpha慢慢调大，召回率上升，我认为这个参数达到了优化模型的目的。

思考题

有什么其他方法可以解决数据集非线性可分的问题？

既然用一条直线无法分割非线性可分的数据集，那只有走曲线救国路线了，提前试了一下用SVM

AI基于Matlab Percetron Learning Algorithm——感知学习算法_第19张图片

验证集集划分.png

AI基于Matlab Percetron Learning Algorithm——感知学习算法_第20张图片

svm.png

解释四个指标的用处和意义。

准确率，它计算的是对于给定的测试数据集，分类器正确分类的样本数与总样本数之比。

精确率Precision，它计算的是所有"正确被检索的item(TP)"占所有"实际被检索到的(TP+FP)"的比例.

召回率Recall，它计算的是所有"正确被检索的item(TP)"占所有"应该检索到的item(TP+FN)"的比例。

一般来说，Precision 就是检索出来的条目中（比如：文档、网页等）有多少是准确的，Recall就是所有准确的条目有多少被检索出来了。

我们当然希望检索的结果P越高越好，R也越高越好，但事实上这两者在某些情况下是矛盾的。比如极端情况下，我们只搜出了一个结果，且是准确的，那么P就是100%，但是R就很低；而如果我们把所有结果都返回，那么必然R是100%，但是P很低。

因此在不同的场合中需要自己判断希望P比较高还是R比较高。如果是做实验研究，可以绘制Precision-Recall曲线来帮助分析。

准确率，我们的确可以在一些场合，从某种意义上得到一个分类器是否有效，但它并不总是能有效的评价一个分类器的工作。举个栗子,google抓取了argcv 100个页面，而它索引中共有10,000,000个页面,随机抽一个页面，分类下,这是不是argcv的页面呢?如果以accuracy来判断我的工作，那我会把所有的页面都判断为"不是argcv的页面",因为我这样效率非常高(return false,一句话),而accuracy已经到了99.999%(9,999,900/10,000,000),完爆其它很多分类器辛辛苦苦算的值,而我这个算法显然不是需求期待的,那怎么解决呢?这就是precision,recall和f1-measure存在的意义。还有很多判断分类器是否优秀的指标，如AP和mAP(mean Average Precision)和ROC&AUC。

AI基于Matlab Percetron Learning Algorithm——感知学习算法

Percetron Learning Algorithm——感知学习算法。

算法原理

抽象模型

评测指标

算法伪代码

原始PLA伪代码

Pocket-PLA伪代码

小数据集验证模型

关键代码和注释

实验结果和评测指标

评测指标图

评测说明

设计PLA二分类模型结果分析

优化点

思考题

你可能感兴趣的:(AI基于Matlab Percetron Learning Algorithm——感知学习算法)