数据结构之二叉搜索树、AVL自平衡树

前言

最近在帮公司校招~~ 所以来整理一些数据结构方面的知识，这些知识呢，光看一遍理解还是很浅的，看过跟动手做过一遍的同学还是很容易分辨的哟~

一直觉得数据结构跟算法，就好比金庸小说里的《九阳神功》，学会九阳神功后，有了内功基础，再去学习其他武功，速度就有质的提升

内容大概包含这些，会分多篇文章来整理：

1. 二叉搜索树
2. 平衡二叉树（AVL）
3. 二叉堆
4. 堆排序
5. 四叉树
6. 八叉树
7. 图，深度优先DFS、广度优先BFS
8. 最短路径

二叉树

二叉树，也就是每个节点最多有两个孩子的树。多用于搜索，查找，还有可以用来求最短编码的哈弗曼树，也称为最优二叉树。

二叉排序/搜索树

如图，树的每个有孩子的节点都满足：左节点的值<根节点的值<右节点的值条件的树，称为二叉排序树，也叫二叉搜索树。

如果对这个树进行中序遍历，就能得到一个排序的数列，非常简单，下面贴出插入操作跟遍历的代码
插入操作

        public void Add(BinaryTree node)
        {
            if (node.Value < Value)
            {
                if (this.Left != null)
                {
                    this.Left.Add(node);
                }
                else
                {
                    this.Left = node;
                }
            }
            else
            {
                if (this.Right != null)
                {
                    this.Right.Add(node);
                }
                else
                {
                    this.Right = node;
                }
            }
        }

中序遍历输出排序列表

        public void InOrder(List list)
        {
            if (Left != null)
            {
                Left.InOrder(list);
            }
            
            list.Add(this.Value);
            
            if (Right != null)
            {
                Right.InOrder(list);
            }
        }

但是二叉排序树极端的情况，效率会变成链表线性结构，这样查找起来时间复杂度会变成O(n)，就失去了树形结构的意义，如图：

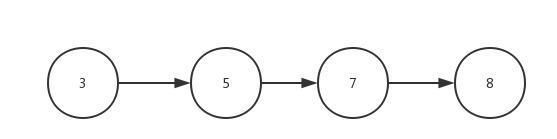
这时就要引出我们的另外一种二叉树树结构了

平衡二叉树

平衡二叉树（AVL）简单来说就是插入的时候，要保证子节点的平衡，别老往一边一直插入下去，那样又成了链表效率了

首先来搞懂这个几个定义
平衡因子：即左子树的高度减去右子树的高度
平衡二叉树上所有节点的平衡因子都必须为：-1、0和1。否则该二叉树就不是平衡二叉树
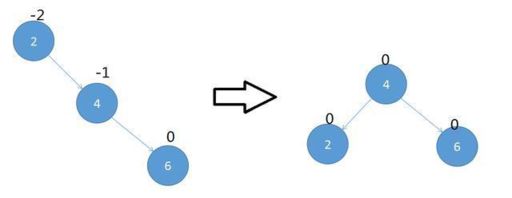
如下图，图左边是一颗平衡二叉树，图右根节点平衡因子为-2，则不是平衡二叉树

如何保持树的平衡
每当插入一个节点的时候，都检查这次插入是否会破坏平衡性，若是，则找出最小不平衡子树，在保持二叉排序树的前提下，进行相应旋转，使之成为新的平衡子树。
通常会有四种旋转情况：

单向右旋平衡处理

也有地方称为Left Left旋转，是不是觉得很奇怪，一下左，一下右边的，它估计是想把你转晕，好套出你的花呗密码。

那么到底是什么意思呢，请看下图

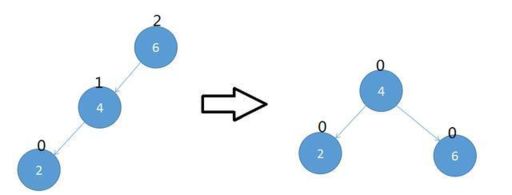
这棵树有三个节点：6，4，2

我们把节点2当成是最新插入进来的节点，由于这个节点2的插入，导致节点6的平衡因子变成了2，不符合-1、0、1的规定，破坏了平衡性，所以我们需要对节点6进行右旋转，而节点2又是节点6的Left节点的Left节点，所以也称为LL旋转。

右旋操作

也就是如果结点6的左孩子节点4有右孩子，则将节点4的右孩子变成节点6的左孩子，最后将节点6变成节点4的右孩子

单向左旋平衡处理
左旋平衡处理也叫RR旋转，是LL的镜像操作

双向旋转（先右后左）平衡处理 (Right Left)
为什么会有这种情况出现呢，因为我们的平衡树，首先也是一颗二叉排序树，必须满足左节点<根节点<右节点的插入规则。

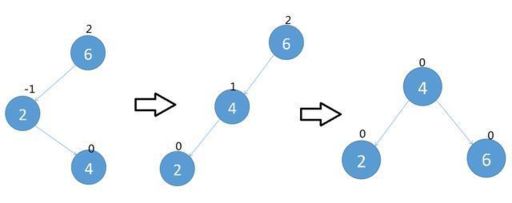
所以如下图，节点4插入导致树失去平衡，单向旋转已经不能满足要求了，需要先让节点6右旋，然后再把节点2左旋

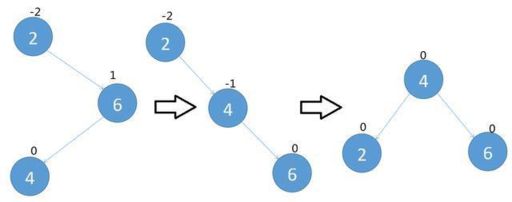
双向旋转（先左后右）平衡处理 (Left Right)
同理，是RL的镜像操作

代码实现

        //右旋转
        public BinaryTree RightRotate(BinaryTree root)
        {
            BinaryTree lchild = root.Left;
            root.Left = lchild.Right;
            lchild.Right = root;
            return lchild;
        }

        //左旋转
        public BinaryTree LeftRotate(BinaryTree root)
        {
            BinaryTree rchild = root.Right;
            root.Right = rchild.Left;
            rchild.Left = root;
            return rchild;
        }

        //先左后右旋转
        public BinaryTree LeftRightRotate(BinaryTree root)
        {
            root.Left = root.Left.LeftRotate(root);
            return RightRotate(root);
        }

        //先右后左旋转
        public BinaryTree RightLeftRotate(BinaryTree root)
        {
            root.Right = root.Right.RightRotate(root);
            return LeftRotate(root);
        }
        
        //计算平衡因子，取绝对值
        public int Balance(BinaryTree root)
        {
            int val = 0;
            if (root.Left != null) val += Height(root.Left);
            if (root.Right != null) val -= Height(root.Right);
            return Math.Abs(val);
        }

        //计算树的高度
        public int Height(BinaryTree root)
        {
            int leftHeight = 0;
            int rightHeight = 0;
            if (root != null && root.Left != null)
            {
                leftHeight += Height(root.Left);
            }
            if (root != null && root.Right != null)
            {
                rightHeight += Height(root.Right);
            }
            return rightHeight > leftHeight ? ++rightHeight : ++leftHeight;
        }

插入操作

        public BinaryTree Inster(BinaryTree root, int key)
        {
            if (root == null)
            {
                root = new BinaryTree(key);
            }
            else if (key < root.Value)//插入到左边
            {
                root.Left = Inster(root.Left, key);

                if (Balance(root) > 1)//插入左节点导致树失衡了
                {
                    if (key < root.Left.Value)//LL处理，右旋
                    {
                        root = RightRotate(root);
                    }
                    else
                    {
                        root = LeftRightRotate(root);//LR处理，先左后右
                    }
                }
            }
            else
            {
                root.Right = Inster(root.Right, key);

                if (Balance(root) > 1)//插入右节点导致失衡
                {
                    if (key > root.Right.Value)//RR处理， 左旋
                    {
                        root = LeftRotate(root);
                    }
                    else
                    {
                        root = RightLeftRotate(root);//RL处理，先右后左
                    }
                }
            }
            return root;
        }

使用平衡二叉树后，查询起来时间复杂度就从O(n)变为了O( log n)。

总结

平衡二叉树的优点在于因为树结构维护的较好，所以搜索查询速度很快，但在插入，删除的时候，为了保持树的平衡会做一次或多次旋转。
适合用于插入删除操作少，而搜索操作很多的情况。

为了减少插入，删除在旋转方面的消耗，另一种自平衡树结构出现了

它就是：红黑树
红黑树不追求"完全平衡"，即不像AVL那样要求节点的 |平衡因子| <= 1，它只要求部分达到平衡，但是提出了为节点增加颜色，红黑是用非严格的平衡来换取增删节点时候旋转次数的降低，任何不平衡都会在三次旋转之内解决，而AVL是严格平衡树，因此在增加或者删除节点的时候，根据不同情况，旋转的次数比红黑树要多。

学会了AVL在去看红黑树也就很简单了~~

参考

https://www.cnblogs.com/sench/p/7786718.html
https://baijiahao.baidu.com/s?id=1577200621749785094&wfr=spider&for=pc