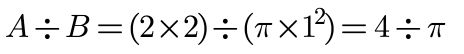圆周率π可能是我们小孩子接触最早的神奇数字,对数学世界的困惑最早就从这里开始。这篇文章将试图从一个小学生的角度科学的解释圆周率的计算方法。
引子
“圆周率是怎么计算出来的?”
“用圆规画个圈,直尺测量圆规两个角之间的距离就是半径,乘以2就是直径;再用绳子贴紧这个圈绕一周,然后把绳子拉直,直尺测量这个绳子长度,最后用绳子长度除以直径就是圆周率派的值。”
——这个回答似乎是完美的,但不好意思,您把数学变成了物理。物理学是从实践中总结规律,总结探索真理;而数学是完全从逻辑中探索规律,数学是不须要实践来验证的。
“圆周率是怎么计算出来的?”
“在很古老的时候,各个国家都认为圆周长是直径的3倍,这个就导致很多测量都不准确,后来我国伟大的魏晋时期数学家祖冲之,发明了割圆术,把派计算到了3.1415926和3.1415927之间,领先了欧洲西方国家1000多年..."
——这个回答更加糟糕,是典型的教孩子答非所问,打太极,你不是数学老师,你是历史老师,是爱国主义政治老师,根本就没回答孩子的问题。
关于祖冲之,这里犯了严重的科学错误,首先,割圆术是汉代刘徽最早提出的;其次,割圆术本身还是物理实践型的测量方法,不可能把π计算到第七位;最后,祖冲之到底用什么办法改进了割圆术?他的技术已经失传,科学家们比较靠谱的看法是,祖冲之的π精度是猜出来的,对他之前的算法进行平均优化加测量验证,最后得到这么一个7位精确度。——这明显不是真正的数学方法,真正提出π的合理计算方法的是比祖冲之晚200来年的古希腊物理学家阿基米德,他以纯数学的方式提出π的值小于22/7而大于223/71 。
科学的方法比正确的答案更重要,下面介绍一种利用Goc实现的比较容易理解的计算π的方法。
从埃及人的谷粒说起
远早于阿基米德和祖冲之,古代埃及人是这样测量圆面积的,用圆规在地上画一个正方形,然后在正方形内画一个最大的圆(内接圆),画好之后在正方形地面上均匀的铺满谷粒,然后把圆里面的谷粒取出来数一数有多少颗,再把剩下在正方形四个角的谷粒取出来数一数。
int main()
{
p.rr(400,400,8);
p.oo(200,12);
for(int i=0;i<2000;i++){
p.move(rand()%400-200,rand()%400-200);
p.oo(5,5);
}
}
假设谷粒铺满,所有谷粒数量(黄色点)为A,暗绿色圆形背景上的谷粒(黄色点)数量是B颗,整个方形的边长是2,圆半径是1,那么全部谷粒是圆内谷粒多少倍,长正方形的面积就是圆面积的多少倍,根据圆的面积公式,圆的面积π乘以半径平方(稍后文章中会细谈这个公式的证明),我们有:
也就是:
所以,我们只要数数谷粒就能计算出π了。
且慢,这不也是物理实践方法吗?
使用网格代替谷粒
数谷粒的方法很不科学,我们把这个方法几何图形化,看下图:
int main()
{
p.rr(400,400,8);
p.oo(200,12);
for(int x=0;x<40;x++){
for(int y=0;y<40;y++){
p.move(-195+x*10,195-y*10);
p.r(10,10,0);
p.oo(1,1);
}
}
}
我们用均匀分布的黑色小格子代替谷粒,但也发现有很多格子是一半在圆里,一半在圆外,这怎么数呢?
改变一下思想,我们按照格子中心的红点算,如果红点在圆里面我们就认为格子也在圆里面。
我们修改一下代码,让格子少一些:
int main()
{
p.rr(400,400,8);
p.oo(200,12);
int gezi=50; //每个格子的边长大小
int huafen=400/gezi; //横向、竖向划分多少格子
for(int x=0;x数一下红点,总计64个,圆内52个,使用刚才的公式计算:
我们得到圆周率是3.25,虽然比祖冲之差了很多,但是我们相信,格子越小越多,那么就一定越精确,不信你可以数数看上面那个密密麻麻40x40一共1600个格子的,用它得到的圆周率就是3.14,有些红点可能看不准到底是圆内还是在圆外,可能会有一点点误差,这已经达到汉朝数学家刘徽计算的精度了!
格子越小,精度越高,但问题来了,成千上万的格子怎么数的过来啊?如何判断红点在圆里面,靠眼睛是不科学的。
圆和勾股定理
什么是圆?圆的定义是什么?
圆是所有到圆心的距离小于半径的点的集合。
换句话说,圆里面任意一个地方,到圆心的距离都不会比半径大。
int main()
{
p.rr(400,400,8);
p.oo(200,12);
for(int i=0;i<100;i++){
int jiao=rand()%360;
int chang=rand()%200;
p.rt(jiao).fd(chang).o(3,1).bk(chang).lt(jiao);
}
}
那么,怎么计算蓝色线的长度呢?使用勾股定理。
勾股定理是说任何直角三角形,斜边长度的平方都等于两个直角边分别平方再相加。
下面我们把图放到圆里面看:
int main()
{
p.showXY(1);
float xian=200; //斜边长,也是半径长
p.o(xian,12);
float jiao=36;
float hudu=jiao/180*M_PI; //转为弧度
float gou=sin(hudu)*xian; //对边直角边长
float gu=cos(hudu)*xian; //邻边直角边长
p.c(0);
p.rt(90-jiao).fd(xian).rt(90+jiao).fd(gou).rt(90).fd(gu);
}
我们看到a和b正好是圆上红点的竖向和横向位置,c正好是半径,所以一个点如果在圆里面,那么它到圆心的距离c的平方一定小于半径的平方,而我们的圆的半径是1,那么就是距离c的平方小于1的点就一定在圆里面。
也就是说,圆里面的点
否则就是圆外面的点。
判断点是否在圆内?
利用勾股定理和圆的关系我们改进计算π的代码,我们把jisuanpi这个函数单独出来,根据格子大小gezi参数画格子。
- 先创建了格子总数zongshu和圆内格子数yuannei两个变量。
- 然后在画每个格子的时候判断这个格子的横向b平方加竖向a平方是否小于圆半径200的平方
- 如果小于就说明这个点在圆内,把yuannei加1
- 最后画好所有点最终计算4/(zongshu/yuannei)就是π的近似值了。
格子越小计算越准,但计算也越慢,如果输入0.1可能需要十几秒才能算出来。
float jisuanpi(float gezi){
float huafen=400/gezi; //横向、竖向划分多少格子
float zongshu=huafen*huafen;//格子总数
float yuannei=0; //圆内点数初始是0,下面加进来
for(int x=0;x2){ //格子太小不画点
p.oo(2,5);//黄色
}
}else{
if(gezi>2){//格子太小不画点
p.oo(2,1);//红色
}
}
}
}
return 4/(zongshu/yuannei);
}
int main()
{
for(int i=0;i<1000;i++){
float a=10;
p << "请输入格子大小1~100:";
p >> a;
p.cls();
if(a>2){
p.rr(400,400,8);
p.oo(200,12);
}else{//格子太小就直接画颜色
p.rr(400,400,1);
p.oo(200,5);
}
float pi=jisuanpi(a);
char str[10];//这两行是把小数变为字符串,突破只显示两位小数的限制
gcvt(pi, 10, str);
p.move(0,-220);
p << str;
p.move(0,0);
}
}
结语
上面的方法并不能真正算出π的精确值,只是知道,格子越小,小数点后面越精确。这也是π最神奇的地方,的确存在那么一个数值,我们也知道算法,但是我们永远也没法精确知道它是多少,因为我们只有在格子无限小的时候才能算出这个值。
所有的科学家也和我们一样,他们也用了各种算法来计算,即使利用最强劲的计算机把π算到了小数点几亿位几十亿位,也还没有算完。
甚至我们至今不能确定π是不是有可能像10/3=3.333333这样,或者像10/7= 2.142857142857142857...这样循环,我们不知道。也许我们把π计算到数亿亿亿小数之后才会发现它的神奇规律呢?
这篇文章其实还有几个遗留问题:
勾股定理需要证明吗?当然需要。任何定理都必须经过科学证明。勾股定理证明方法很简单,可以直接百度到。
圆面积等于π乘以半径的平方,为什么是这样?怎么证明?仍然需要微积分思路,在下一篇文章中我会尝试找到最简单的解说方法。
科学家真的是按照我们这样分隔格子的方法计算π的吗?割圆术到底是怎么回事?在下一篇文章中我会慢慢和大家一起来用Goc学习新的思路新的方法,用更加科学的算法计算π,比如泰勒展开式。
请参照Goc-圆周率“π”是怎么计算来的?-续
致力于让一切变得通俗易懂
如果您发现文章错误,请不吝留言指正;
如果您觉得有用,请点喜欢;
如果您觉得很有用,感谢转发~
END