Exercise11

Problem4.19：Study the behavior of our model for Hyperion for different initial conditions.Estimate the Lyapunov exponent .Examine how this exponent varies as a function of the eccentricity of the orbit.

Hyperion_true.jpg

公式：

1.gif

2.gif

正文

import numpy as np
import pylab as pl
import math
class hyperion:
    def __init__(self,x0=1,y0=0,vx=0,vy=2*math.pi,dt=0.0001,total_time=10,initial_theta=0,initial_omega=0):
        self.x=[x0]
        self.y=[y0]
        self.r=[math.sqrt(x0**2+y0**2)]
        self.vx=[vx]
        self.vy=[vy]
        self.dt=dt
        self.t=[0]
        self.tt=total_time
        self.th=[initial_theta]
        self.om=[initial_omega]
        self.a=0
        self.b=0
        self.ecc=0
        self.dtheta=[]
    def run(self):
        while self.t[-1]math.pi:
                self.th[-1]-=2*math.pi
            elif self.th[-1]<-math.pi:
                self.th[-1]+=2*math.pi
            self.t.append(self.t[-1]+self.dt)
        self.a=(max(self.x)-min(self.x))/2
        self.b=(max(self.y)-min(self.y))/2
        self.ecc=math.sqrt(math.fabs(self.a**2-self.b**2))/self.a
    def showth(self):
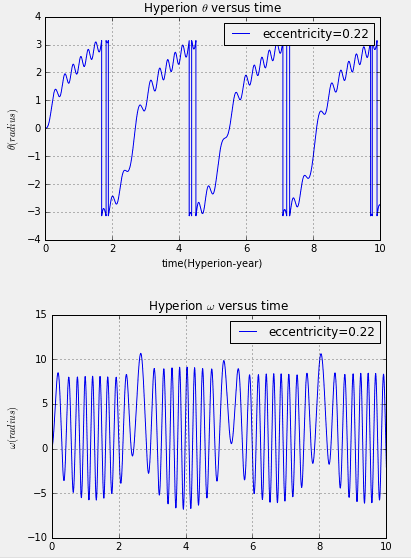
        pl.title("Hyperion $\\theta$ versus time")
        pl.xlabel("time(Hyperion-year)")
        pl.ylabel("$\\theta (radius)$")
        pl.xlim(0,10)
        pl.plot(self.t, self.th,label="eccentricity=%.2f"%self.ecc) 
        pl.legend()
        pl.grid(True)
        pl.show()
    def showom(self):
        pl.title("Hyperion $\\omega$ versus time")
        pl.xlabel("time(Hyperion-year)")
        pl.ylabel("$\\omega (radius)$")
        pl.xlim(0,10)
        pl.plot(self.t, self.om,label="eccentricity=%.2f"%self.ecc)  
        pl.legend()
        pl.grid(True)
        pl.show()
#plot theta or omega versus time
a=hyperion()
a.run()
a.showth()
a=hyperion()
a.run()
a.showom()
#plot delta theta versus time and calculate the lyapuniv exponent
class qwer(hyperion):
    def haha(self):
        _d=0.01
        _vy=2*math.pi-1.1
        a=hyperion(vy=_vy)
        a.run()
        print(a.ecc)
        tempth1=a.th
        a=hyperion(vy=_vy,initial_theta=_d)
        a.run()
        tempth2=a.th
        for i in range(len(tempth2)):
            a.dtheta.append(math.log(math.fabs(tempth2[i]-tempth1[i])))
        pl.plot(a.t,a.dtheta,label="eccentricity=%.4f"%a.ecc)
        dd=[]
        tt=[]
        for j in range(len(a.dtheta)):
            dd.append(a.dtheta[j])
            tt.append(a.t[j])
        z=np.polyfit(tt,dd,1)
        p=np.poly1d(z)
        print(p)
        linspx=np.linspace(0,8)
        linspy=z[0]*linspx+z[1]
        pl.plot(linspx,linspy,label="lyapunov exp=%.4f"%z[0])
        pl.xlabel("time(Hyperion-year)")
        pl.ylabel("$\\Delta\\theta(radius)$")
        pl.title("Hyperion $\\Delta\\theta$ versus time for initial $\\Delta\\theta$=%.3f"%_d)
        pl.legend()
b=qwer()
b.haha()

结论：

3.gif

4.gif

5.gif

6.gif

可见Lyapunov exponent会随轨道偏心率的变化而改变。

致谢：
感谢秦大粤同学的热心帮助！