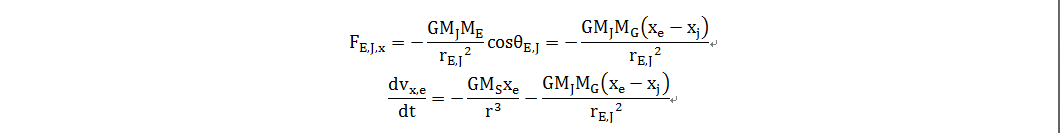exercise11：problem 4.19、20

一、摘要

1、研究了简单的太阳、木星（Jupiter）和地球的三体运动问题，由于相对而言，木星质量在八大行星里是最大的，所以它经过地球时，可能对地球运动造成一定影响，于是我用书上的步骤模拟绘制出来他们的运动轨迹，并假设计算方法不变，木星质量变为原来的10倍、1000倍时，看运动轨迹变化

2、模拟了木星对处于它的共振带的小行星运动影响（我画的是处于2/1 Kirkwood gap的小行星）

3、探究了Hyperion的运动状态。Hyperion 是土星（Saturn）的一颗卫星，它是一颗形状奇怪的卫星（哑铃状），我绘制了它的自转角度Θ和角速度ω随时间的变曲线，探究了它的初始化改变带来的混沌状态，探究了书上习题problem 4.19、4.20

二、背景介绍

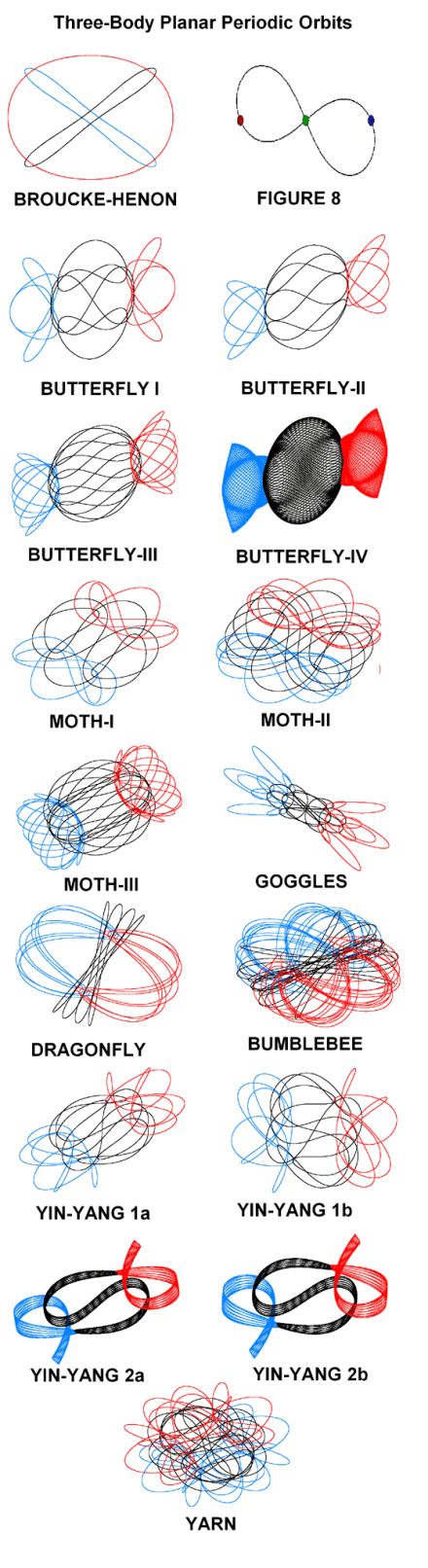
1900年，数学家希尔伯特在他著名的演讲中提出了23个困难的数学问题以及两个典型例子，第一个是费尔马猜想，第二个就是所要介绍的N体问题的特例——三体问题。对于20世纪数学的整体发展，这两个例子所起的作用要比23个问题中的任何一个都更加巨大。最终，费尔马猜想在1994年被美国的怀尔斯解决，而三体问题却仍然是数学大厦上的一朵乌云，挥之不去。

一般的三体问题，每一个天体在其他两个天体的万有引力作用下，其运动方程都可以表示成6个一阶的常微分方程。因此，一般三体问题的运动方程为十八阶方程，必须得到18个积分才能得到完全解。然而，现阶段还只能得到三体问题的10个初积分，远远不足以解决三体问题。

我们常说的“三体问题无解”，准确地来说，是无解析解，意思是三体问题没有规律性答案，不能用解析式表达出来，只能算数值解，没有办法得出精确值。然而对于三体问题的数值解，时间会无限放大初始的微小误差，因此数值法几乎没有办法预测当时间趋于无穷时，三体轨道的最终命运。而这种对于轨道的长时间行为的不确定性，就被称为“混沌”现象。三体问题理论上是不可解的，只能发现一些特解，

人类耗费多少实际解决这个问题，终究是证明自己在上帝面前是多么的渺小与愚蠢

。。。。。。

但谁叫我们是人类呢！

这里讨论及其简单粗暴的对于太阳、木星（Jupiter）和地球的三体运动问题，木星受到的沿x轴方向的力和沿x轴方向的加速度代数表达如下

沿y轴方向的力和加速度同样形式

地球所受的力和加速度一样可以这样求出来，再运用我们已经运用多次的Euler-Cromer方法，我们可以一步一步模拟出运动轨迹，具体参数为

Kirkwood Gaps 产生的原因是该轨道上运动的行星会与周期木星“共振”，由于木星质量较大，对其他行星运动产生影响较大，特别是共振态上的，运行一段时间后会飞出去。

我取的小行星处于2/1 gap处，参数为a=3.276 AU,v=3.471 AU/yr

Hyperion绕着土星（Saturn）运动，我们模拟时可看做用一根无质量硬杆连接的哑铃状物体，作用在质点m1上的力可以写成

以质心为原点，作用在m1上的力矩和由此推出的近似角速度为

据此一步步运算，作图

三、主体

1、太阳、木星（Jupiter）和地球的三体运动问题

代码：三体轨迹

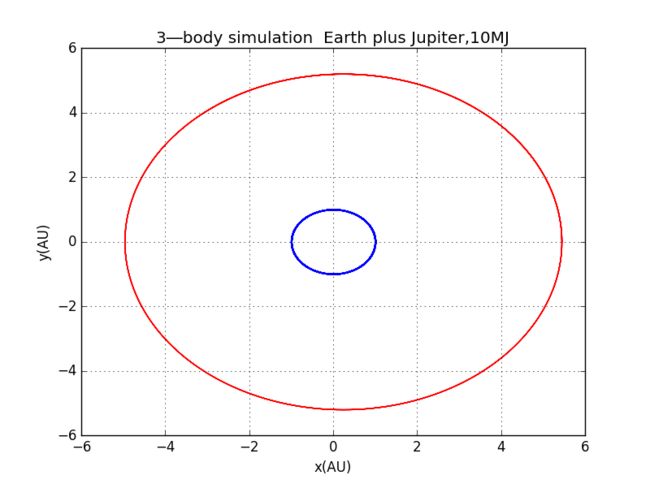
当我们把Jupiter的质量变为原来的10倍甚至1000倍时，变化产生了

质量变为10倍时，地球运动轨迹变化还无法察觉

变为1000倍时，虽然Jupiter相对太阳的质量不可以忽略，太阳运动也会显著变化，理论上我们的算法将要改变，但若不变算法，我们依然可以定性的探究一下，可以见到地球运动变得混沌，然后突然一下飞了出去，可怕！

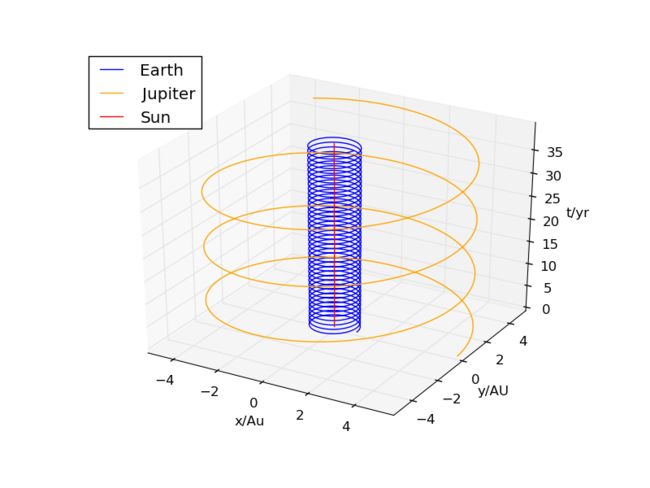
不会用vpython，所以可耻地借用别人的3Dvpython图，可以更直观的展现这种变化

MJ

1000MJ

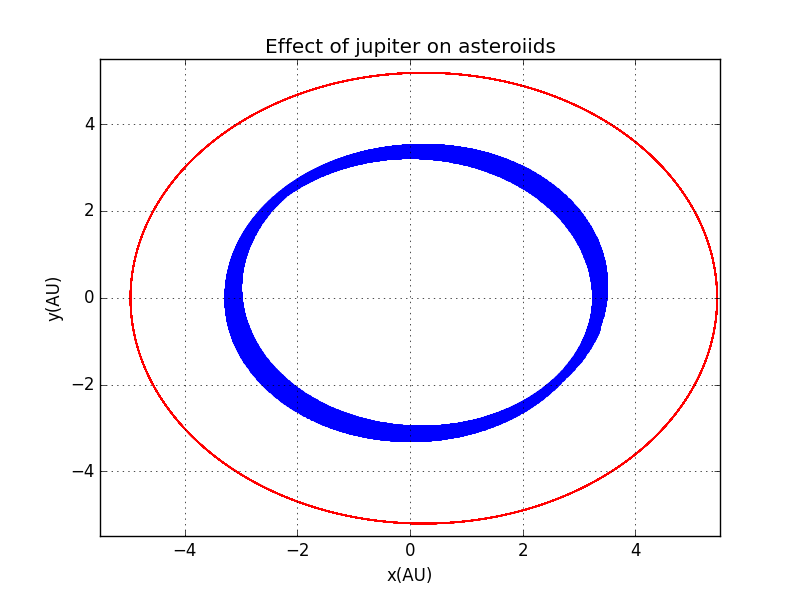
2、Resonance    木星对处于它的共振带的小行星运动影响

代码：Resonance in solar system

可见影响还是有的，轨迹不再重合，据书上所说，小行星将处于共振态很长一段时间，然后突然剧变， 最终偏离原轨道。

3、Hyperion的混沌状态

代码：Hyperion的Θ和ω随时间变化

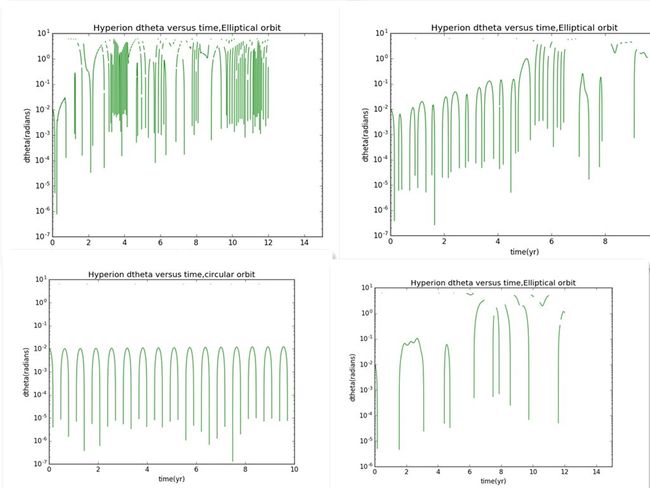
Hyperion的dΘ随时间的变化

Hyperion的dΘ随时间的变化，无角度限制

---

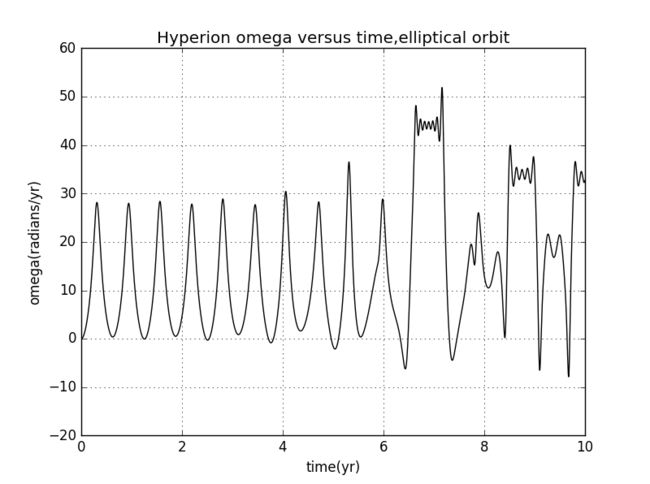
Hyperion的Θ和ω随时间变化

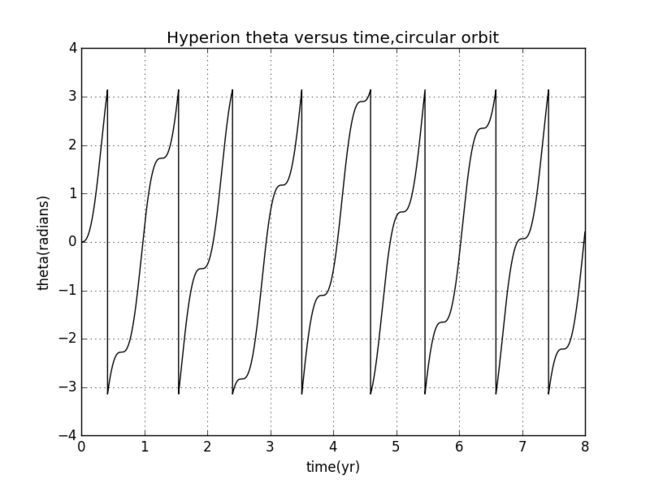
当轨道为圆形即初始的vy=2π HU/Hyperion-year时

轨迹为圆时运动是相当规律的

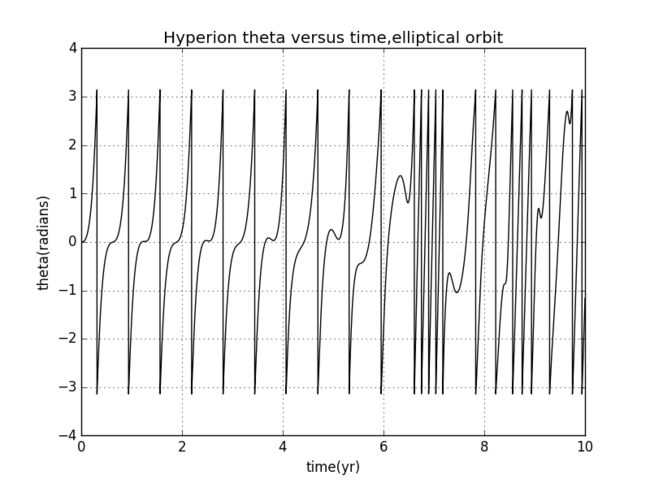
若改变初始vy=5HU/Hyperion-year,轨迹变成椭圆

混沌运动产生，我们进一步探究，改变初始条件，使两个运动的初始角度Θ差0.01，即dΘ=0.01

并作出dΘ随时间的变化图

Hyperion的dΘ随时间的变化

圆形轨迹

椭圆轨道

我取的初始值统一x=1,y=0,vx=0,所以取不同初始vy,可以使椭圆离心率发生变化（其中vy=2π时是圆），为探究不同离心率e对Lyapunov  exponent的影响，我取了vy=4、5、2π、7

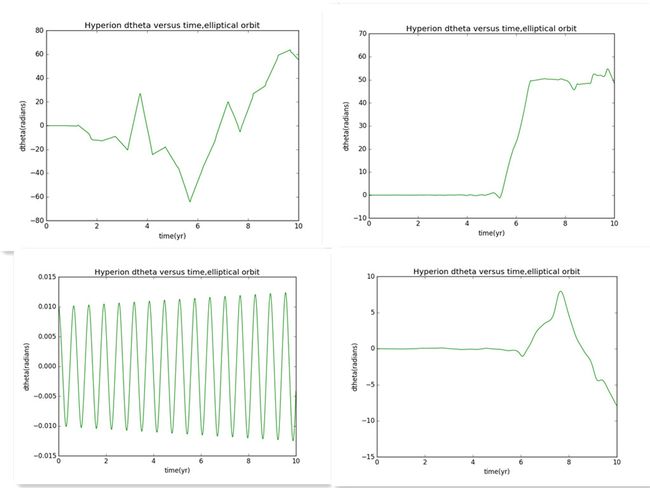
当我把对角度的限制去掉以后，即角度不再是限制于-π~+π时，，同样条件得出的图是（PS：纵坐标不再取log值）

Hyperion的dΘ随时间的变化，无角度限制

四、结论

1、三体运动是复杂无解的，但只考虑非常简化的太阳、木星（Jupiter）和地球的三体运动时，可以看出木星对地球的影响十分小，但如果把木星的质量变为原来的1000倍，那影响将十分巨大，地球也将不再是现在这个样子

2、木星对处于它的共振带的小行星运动有较大影响，小行星将处于共振态很长一段时间，然后突然短时间内剧变， 最终偏离原轨道。

3、Hyperion绕着土星公转，但它的自转角速度是混沌的，若轨道是圆形轨道，Θ、ω都是周期的，轨道变为椭圆，混沌现象出现。去掉角度的限制后，图中还有一些谷，是因为当角度大的一方的角速度从正变为负的时候，角度差会减小所致。

五、致谢

1、计算物理课本

2、百度百科

3、郭潇同学的v-python图