运行要求
运行时间限制: 2sec
内存限制: 1024MB
原题链接
AtCoder Context ABC 112 C Pyramid(金字塔)
题目
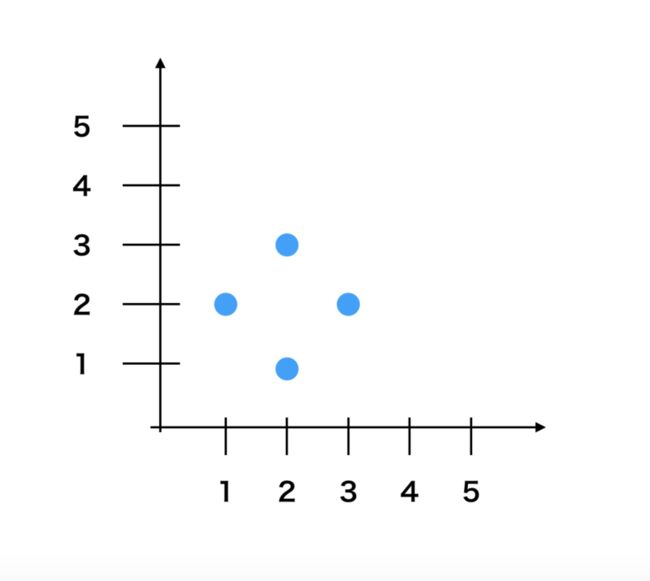
在古代夜郎国，夜郎国的君王为了展示自己的权威，决定修建金字塔。这个金字塔坐落在平面直角坐标系中。金字塔的中心坐标为(Cx,Cy),高度为H。对于金字塔的其他坐标（X，Y）来说，金字塔位于坐标X，Y的点上的高度满足以下条件
max(H - |Cx - X| - |Cy - Y|,0)
探险家施塔克接到一个任务，他需要探测金字塔的中心点的高度和坐标。现在施塔克手上有的信息是这些。
- 中心点的坐标Cx，Cy是介于1和100之间（包括1和100的整数）。
- 除了以上的信息以外还有N条信息。N条信息中的第i条信息，指明了第i个点的坐标(xi,yi)以及该点在金字塔上的高度hi
通过以上信息可以找出金字塔的中心点和高度，请求出这些值
输入前提条件
- 1 <= N <= 100 N为整数
- 0<= xi,yi <= 100
- 0 <= hi <= 1000000000
- N个点的坐标(x1,y1),(x1,y2),(x3,y3)....(xN,YN)每个坐标点不重合
- 根据以上条件刚好可以求出一个点能够满足金字塔中心点的要求
输入
输入都以以下标准从命令行输入
x1 y1 h1
x2 y2 h2
x3 y3 h3
.
.
.
xN yN hN输出
输出特定的中心坐标Cx，Cy，及其高度Ch，用空格间隔
例1
输入
4
2 3 5
2 1 5
1 2 5
3 2 5输出
2 2 6以上的情况，中心点坐标为（2，2），中心点高度为6，满足条件
例2
输入
2
0 0 100
1 1 98输出
0 0 100以上的情况，中心点坐标为（0，0），中心点高度为100，满足条件
注意中心坐标Cx，Cy是介于0和100之间的数
例2
输入
3
99 1 191
100 1 192
99 0 192输出
100 0 193以上的情况，中心点坐标为（100，0），中心点高度为193，满足条件
解题思路
读懂题目
0. 金字塔的中心点就是说最高点，也就是说金字塔高度的变量H最大的，比所有的ch都要大。当然如果给出坐标点里面存在一个点(ci,cy)就是中心的话，那么该点cy比其他点的cy都要大
1. 首先有一个直角坐标系，上面有好多个点，以例1为例子 
2. 每一个点都带有一个高度，可以看作每个点都带有一个数字
3. max(H - |Cx - X| - |Cy - y|) 这个公式可以看出，金字塔的每个点到中心点的路程 = 该点的高度和中心点高度的差距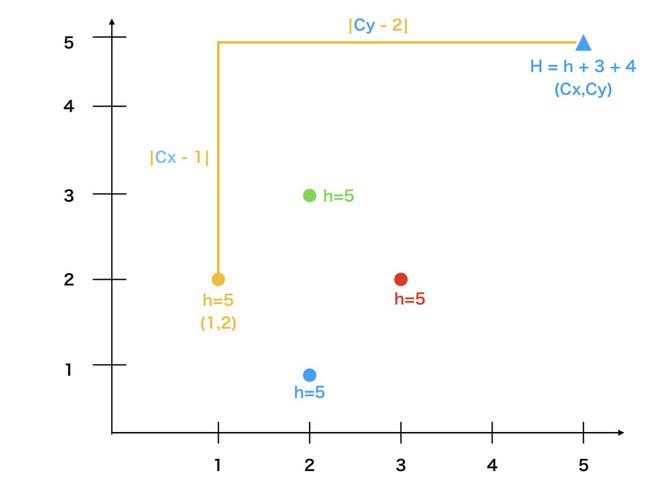 
4. 寻找中心点，用数学方式去求，需要用高难度的数学公式，但是我们是用程序去解决，那么每一个点，看看这个点是不是满足中心点的条件，如果是那么便输出答案
5. 遍历寻找中心点的可能性：xi和yi是介于0到100的值，那么这个坐标系总共有101乘上101个点。那么我们检查每个点是否符合中心点条件的时候，需要遍历给出的N个点，N的最大值也是100。所以最高要遍历101乘上101乘上100次，这对于程序来说要在规定的时间内完成是可行的
6. 如何检查中心点是否符合条件呢
遍历到第i个点的坐标假设为xi,yi
给出的N个点中，每个点都有一个高度cy,有一个坐标cx，cy。那么我们可以求出，这个点到中心的距离distance = |xi - cx| + |yi - cy|
用cy+distance的值可以求出中心点的高度。
当所有点求出的高度不都一致的时候，说明，这个点是不符合中心点要求的。
如图所示，假设黑色的三角形所在的坐标点(5,5)是中心点的话，由黄色的点和红色的点求出的中心点的高度分别是12和10。（5，5）不满足中心点的要求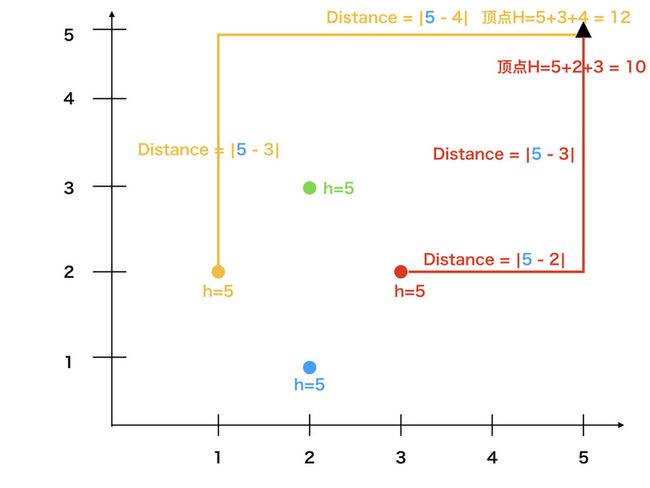
如图所示，假设黑色的三角形所在的坐标点(2,2)是中心点的话，由黄色的坐标点和红色的坐标点和蓝色的坐标点和绿色的坐标点求出的中心点的高度都是6。
说明了坐标点（2，2）满足中心点的要求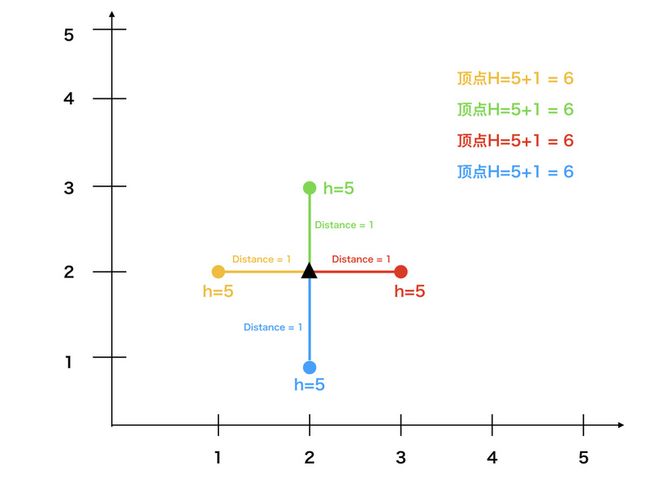
7 还有一点需要注意的是
看看公式
max(H - |Cx - X| - |Cy - y|,0)
也就是说如果某一个坐标点，它和中心点离得非常非常地远。这个时候它的高度也为0
比如中心点在（50，50）的位置，中心点的高度在10，这个点的点坐标是(10,10)
按照公式求这个点的的高度确实为0.
max（10 - 40 - 40， 0） = max(-70,0) = = 0。
但对于这些点，如果我们按照之前的方法去计算中心点的高度的话，就会得到中心点的高度为 (0 + 40 + 40) = 80，这和其他正常坐标点计算出来的中心点高度为10是相矛盾的，这样的话一个合格的中心点就要被pass了。但是对于这种给定的坐标点，计算中心点的高度是不应该举要参考价值的。
所以对于到中心点的距离超过中心点高度的坐标点，我们要忽略，不要纳入中心点的判断。
只有到中心点的距离=中心点高度，h=0的情况，我们才会考虑纳入中心点的判断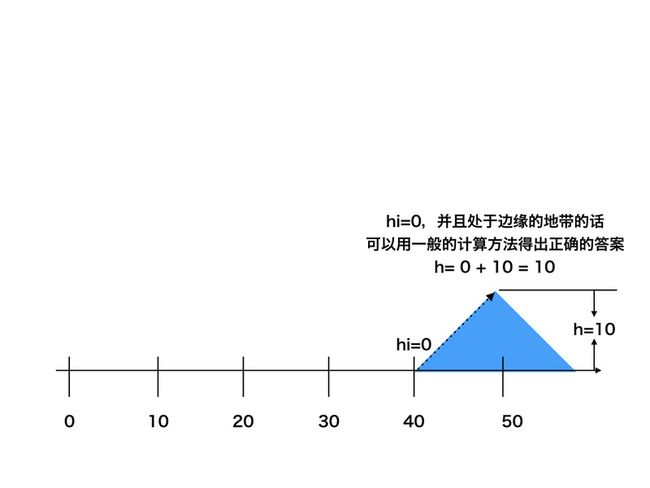 
代码
arr = []
n = int(input())
for i in range(n):
arr.append([int(s) for s in input().split(" ")])
import math
def calculate(n, arr):
for i in range(101):
for j in range(101):
centerH = -100
for ar in arr:
posX = ar[0]
posY = ar[1]
posH = ar[2]
if posH > 0:
if centerH == -100:
centerH = posH + int(math.fabs(i - posX)) + int(math.fabs(j - posY))
continue
tmp = posH + int(math.fabs(i - posX)) + int(math.fabs(j - posY))
if tmp != centerH:
centerH = -2
break
for ar in arr:
posX = ar[0]
posY = ar[1]
posH = ar[2]
if posH == 0:
if int(math.fabs(i - posX)) + int(math.fabs(j - posY)) < centerH:
centerH = -2
break
if centerH != -2:
print(i, j, centerH)
calculate(n, arr)
总结
这道题咋一看很难，但是一旦我们审视条件发现可以用遍历的方法去寻求答案后，我们便可把数学问题转化为for循环的问题。
※ 另外，我会在我的微信个人订阅号上推出一些文章，欢迎关注