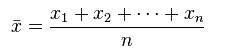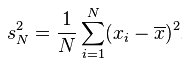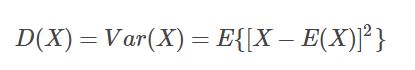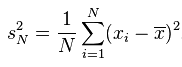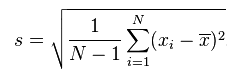我们已经了解概率的基础,概率中通常将试验的结果称为随机变量。随机变量将每一个可能出现的试验结果赋予了一个数值,包含离散型随机变量和连续型随机变量。
掷硬币就是一个典型的离散型随机变量,离散随机变量可以取无限个但可数的数值。而连续变量相反,它在某一个区间内能取任意的数值。时间就是一个典型的连续变量,1.25分钟、1.251分钟,1.2512分钟,它能无限分割。
既然随机变量可以取不同的值,统计学家就用概率分布描述随机变量取不同值的概率。相对应的,有离散型概率分布和连续型概率分布。
对于离散型随机变量x,定义一个概率函数叫f(x),它给出了随机变量取每一个值的概率。
拿出一个骰子,掷到6的概率是f(6) = 1/6,掷到1和6的概率则是f(1)+f(6) = 1/3。
数学期望(均值)
理解一:
在概率论和统计学中,数学期望(mean)(或均值,亦简称期望)是试验中每次可能结果的概率乘以其结果的总和。是最基本的数学特征之一。它反映随机变量平均取值的大小。其公式如下:
xk :表示观察到随机变量X的样本的值。
pk : 表示xk发生的概率。
数学期望反映的是平均水平。通过它,我们能够了解一个群体的平均水平(比如说,一个班平均成绩80)。但另外一个方面,它所包含的信息也是十分有限的,首先是个体信息被压缩了,其次如果单纯看期望的话,是看不出样本的数量。(平均成绩为80,在1人班和100人班的含义是不一样的)
通过这个问题想说明,在刻画群体特征的时候,多个数字特征配合才能达到效果。(上面的例子:可以是 期望 + 数量)
理解二:
在概率论和统计学中,数学期望(mean)(或均值,亦简称期望)是试验中每次可能结果的概率乘以其结果的总和
严格的定义如下:
2.数学期望的含义
这个很重要,我们一定要明白概念的含义,联系到实际的应用场景中表达的真正意义,数学期望的存在是为了表达什么?
答:反映随机变量平均取值的大小
3.数学期望(均值)和算术平均值(平均数)的关系(期望和平均数的关系)
谈谈我对于这两个概念的理解
(1)平均数是根据实际结果统计得到的随机变量样本计算出来的算术平均值,和实验本身有关,而数学期望是完全由随机变量的概率分布所确定的,和实验本身无关。以摇骰子为例,假设我们摇4次骰子,摇出的结果依次为5,5,6,4。设摇出的结果为随机变量X,,则X在这次实验中的平均数(5+5+6+4)/4= 5.而X的期望呢?和这次的实验本身无关,只和X的概率分布有关。X的概率分布如下:
则
E(X) = 1*1/6+2*1/6+3*1/6+4*1/6+5*1/6+6*1/6 = (1+2+3+4+5+6)*1/6 = 3.5
实验的多少是可以改变平均数的,而在你的分布不变的情况下,期望是不变的。
(2)我们可以从概率和统计的角度给出理解
先给出结论,摘自知乎:
如果我们能进行无穷次随机实验并计算出其样本的平均数的话,那么这个平均数其实就是期望。当然实际上根本不可能进行无穷次实验,但是实验样本的平均数会随着实验样本的增多越来越接近期望,就像频率随着实验样本的增多会越来越接近概率一样
如果说概率是频率随样本趋于无穷的极限
那么期望就是平均数随样本趋于无穷的极限
上述表达的意思其实也就是弱大数定理
1期望、方差、标准差
概率论与数理统计中,最基本概念就是均值、方差、标准差,n个样本xi的集合X。具体公式描述为:
对于一维数据的分析,最常见的就是计算平均值(Mean)、方差(Variance)和标准差(Standard Deviation)。
平均值
平均值的概念很简单:所有数据之和除以数据点的个数,以此表示数据集的平均大小;其数学定义为:
在概率论和数理统计中,方差(英文Variance)用来度量随机变量和其数学期望(即均值)之间的偏离程度.方差越大,随机变量的结果越不稳定。常用来评估风险。
方差是各个数据与平均数之差的平方的和的平均数,用字母D表示.
标准差与方差一样,表示的也是数据点的离散程度;其在数学上定义为方差的平方根:
当我们面对一堆数字的时候,我们可以很简单的找出这组数字的中值,也可以很容易算出平均值。但是只有这两个数字还不够,因为这样无法勾勒出这一堆数字整体的“shape”。此时,标准差的作用就可以体现出来了。
标准差是一组数值自平均值分散开来的程度的一种测量观念。一个较大的标准差,代表一组数据里大部分的数值和其平均值之间差异较大;一个较小的标准差,代表这些数值较接近平均值。
两组数的集合 {1, 4, 9, 14} 和 {5, 6, 8, 9} 其平均值都是7,但第二个集合里的数字明显与7距离“更近”,通过公式算出第一个集合的标准差约为4.9,第二个约为1.5。
计算流程如下:首先计算出该组数据里每一个数字与平均值的差,然后将所有的得出差进行平方,接下来求出均值,最后再开方。
为什么用这么复杂的方法来计算标准差呢,这是因为在实践中,我们发现相当多的数据都呈现近似于“正态分布”
简单的说就是呈现正态分布的一组数据中,靠近中间高点的数字出现的概率要远大于在两侧更远地方出现的概率。
在很多情况下统计数据都会呈现正态分布的构造,比如在样本很大、每一个样本又是类似的独立随机事件。例如能力的高低,学生成绩的好坏,人们的社会态度,行为表现以及身高、体重等身体状态都呈现正态分布。
理解正态分布对理解标准差具有重要的意义,回到上面那张钟形曲线图,如果说平均值可以告诉我们这条曲线最高点在什么位置,那么标准差就可以告诉我们这条曲线的宽窄程度。
反过来正态分布也可以用来解释标准差:在一个标准正态分布中,数字出现的概率是固定的。
标准差经常被用来描述价格的波动性,标准差越大说明其偏离均值程度越大,也越罕见,之后回归常态的可能性也在升高。
什么是Variance(方差)
Variance反映的是模型每一次输出结果与模型输出期望之间的误差,即模型的稳定性。反应预测的波动情况。
方差
(variance)是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。在许多实际问题中,研究方差即偏离程度有着重要意义。
方差( D(X)或Var(X) )计算公式如下:
X:表示随机变量。
E(X) : 表示X的期望。
D(X) : 是每个样本值与全体样本值的平均数之差的平方值的平均数
公式逐步解释:[X−E(X)] —> [X−E(X)]22 —> E{[X−E(X)]2}
[X−E(X)] 是计算随机变量中各个值与期望的距离(反映的是以E(X)为基准计算的偏差)。但是只是将偏差进行求和,可能导致结果为0的情况(会产生离散程度较高,评价却为0的情况)。
平方[X−E(X)]2 可避免上述情况发生,但问题依据存在,不同的随机变量(比如,X,Y)之间在此级别是无法进行比较的,因为X,Y的数量空间是不同的(X可能有3个值,Y可能有1000个值),进而导致不具有可比性。
E{[X−E(X)]2} 则是将数量空间进行了统一,使得不同随机变量的方差具有了可比性。
方差单位和数据的单位不一致,没法使用。标准差和数据的单位一致,使用起来方便。具体说下吧。
1.标准差有啥卵用?
方差、标准差
方差这一概念的目的是为了表示数据集中数据点的离散程度;其数学定义为:
标准差与方差一样,表示的也是数据点的离散程度;其在数学上定义为方差的平方根:
为什么使用标准差?
与方差相比,使用标准差来表示数据点的离散程度有3个好处:
表示离散程度的数字与样本数据点的数量级一致,更适合对数据样本形成感性认知。依然以上述10个点的CPU使用率数据为例,其方差约为41,而标准差则为6.4;两者相比较,标准差更适合人理解。
表示离散程度的数字单位与样本数据的单位一致,更方便做后续的分析运算。
在样本数据大致符合正态分布的情况下,标准差具有方便估算的特性:66.7%的数据点落在平均值前后1个标准差的范围内、95%的数据点落在平均值前后2个标准差的范围内,而99%的数据点将会落在平均值前后3个标准差的范围内。
贝赛尔修正
在上面的方差公式和标准差公式中,存在一个值为N的分母,其作用为将计算得到的累积偏差进行平均,从而消除数据集大小对计算数据离散程度所产生的影响。不过,使用N所计算得到的方差及标准差只能用来表示该数据集本身(population)的离散程度;如果数据集是某个更大的研究对象的样本(sample),那么在计算该研究对象的离散程度时,就需要对上述方差公式和标准差公式进行贝塞尔修正,将N替换为N-1:
经过贝塞尔修正后的方差公式:
经过贝塞尔修正后的标准差公式:
公式的选择
是否使用贝塞尔修正,是由数据集的性质来决定的:如果只想计算数据集本身的离散程度(population),那么就使用未经修正的公式;如果数据集是一个样本(sample),而想要计算的则是样本所表达对象的离散程度,那么就使用贝塞尔修正后的公式。在特殊情况下,如果该数据集相较总体而言是一个极大的样本 (比如一分钟内采集了十万次的IO数据) — 在这种情况下,该样本数据集不可能错过任何的异常值(outlier),此时可以使用未经修正的公式来计算总体数据的离散程度。
平均值与标准差的适用范围及误用
大多数统计学指标都有其适用范围,平均值、方差和标准差也不例外,其适用的数据集必须满足以下条件:中部单峰:
数据集只存在一个峰值。很简单,以假想的CPU使用率数据为例,如果50%的数据点位于20附近,另外50%的数据点位于80附近(两个峰),那么计算得到的平均值约为50,而标准差约为31;这两个计算结果完全无法描述数据点的特征,反而具有误导性。
这个峰值必须大致位于数据集中部。还是以假想的CPU数据为例,如果80%的数据点位于20附近,剩下的20%数据随机分布于30~90之间,那么计算得到的平均值约为35,而标准差约为25;与之前一样,这两个计算结果不仅无法描述数据特征,反而会造成误导。
遗憾的是,在现实生活中,很多数据分布并不满足上述两个条件;因此,在使用平均值、方差和标准差的时候,必须谨慎小心。
结语
如果数据集仅仅满足一个条件:单峰。那么,峰值在哪里?峰的宽带是多少?峰两边的数据对称性如何?有没有异常值(outlier)?为了回答这些问题,除了平均值、方差和标准差,需要更合适的工具和分析指标,而这,就是中位数、均方根、百分位数和四分差的意义所在。