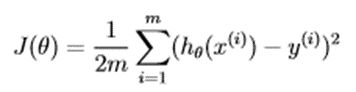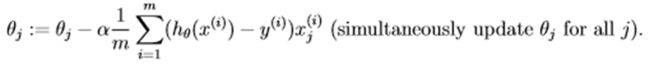Linear-Regression - Shuai-Xie -Github
Part 1: Question
预测在哪个城市开快餐店利润最高
ex1data1.txt （城市人口，快餐店利润）
6.1101,17.592
5.5277,9.1302
8.5186,13.662
7.0032,11.854
5.8598,6.8233
8.3829,11.886
……
Part 2: Plotting data
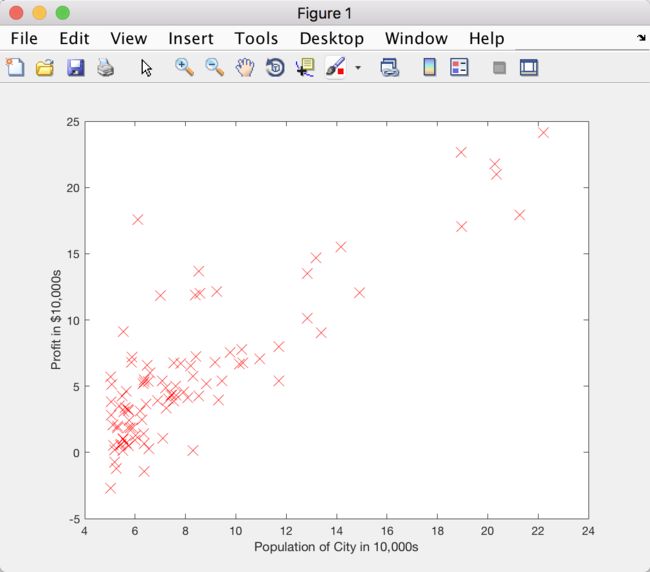
通过散点图可视化数据
%% ======================= Part 2: Plotting data =======================
% 输出样本点散点图
fprintf('Plotting Data ...\n')
data = load('ex1data1.txt'); % 加载数据 csv文件
X = data(:, 1); % X 城市人口 第1列
y = data(:, 2); % y 城市利润 第2列
m = length(y); % 训练集大小
% 调用 plotData 函数做散点图
plotData(X, y);
fprintf('Program paused. Press enter to continue.\n');
pause;
plotData 函数
function plotData(x, y)
% PLOTDATA Plots the data points x and y into a new figure 返回值为空的函数
% 1. plots the data points.
% 2. gives the figure axes labels of population and profit.
figure; % 打开一个空的图片窗口
% 调用 matlab 描点函数 在 figure 打开的窗口上描点
plot(x, y, 'rx', 'MarkerSize', 10); % rx 红十字，10 设置 MarkerSize
% 设置 x, y 轴标签
ylabel('Profit in $10,000s');
xlabel('Population of City in 10,000s');
end
Figure 1: Scatter plot of training data
Part 3: Gradient descent
%% =================== Part 3: Gradient descent ===================
fprintf('Running Gradient Descent ...\n')
% 调整样本并初始化一些值
X = [ones(m, 1), data(:,1)]; % 添加 ones(m, 1) 适配 theta0
theta = zeros(2, 1); % theta = [0,0]
iterations = 1500; % 迭代次数
alpha = 0.01; % 学习率
% 初始情况(theta=0)下的 cost
computeCost(X, y, theta);
% 梯度下降法求最优的 theta
theta = gradientDescent(X, y, theta, alpha, iterations);
% 1500次学习后的 theta
fprintf('Theta found by gradient descent: ');
fprintf('%f %f \n', theta(1), theta(2)); % 分别打印，注意matlab下标从1开始
% 在保留散点的基础上 画出 最终theta 确定的 线性方程
hold on; % keep previous plot visible 保留以前的散点
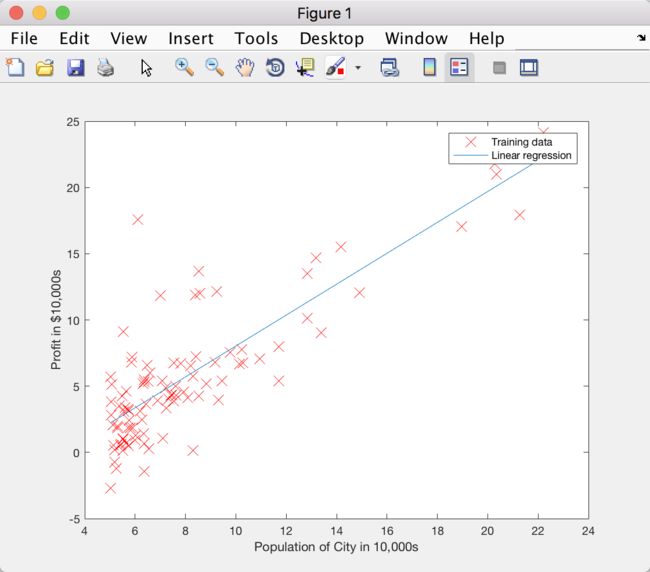
plot(X(:,2), X * theta, '-'); % 用 '-' 表示点，做散点图的时候用的是 'rx'
legend('Training data', 'Linear regression'); % 设置图例分别对应 'rx', '-'
hold off; % not overlay any more plots on this figure 不再画任何点
% 用 theta 预测，城市人口数：35,000 和 70,000
predict1 = [1, 3.5] * theta;
fprintf('For population = 35,000, we predict a profit of %f\n', predict1*10000);
predict2 = [1, 7] * theta;
fprintf('For population = 70,000, we predict a profit of %f\n', predict2*10000);
fprintf('Program paused. Press enter to continue.\n');
pause;
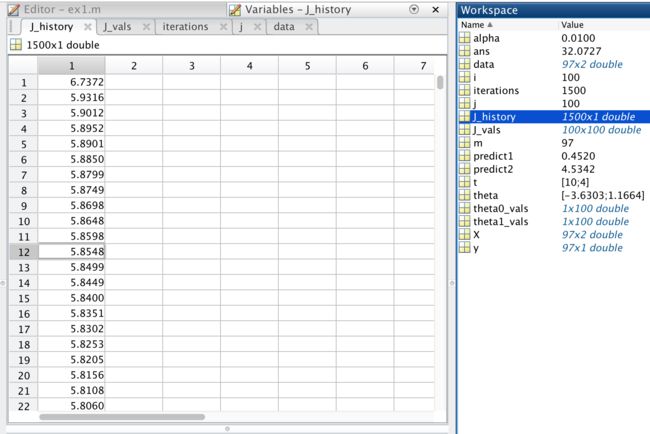
Running Gradient Descent ...
ans =
32.0727
After the last iteration: J = 4.483388
Theta found by gradient descent: -3.630291 1.166362
For population = 35,000, we predict a profit of 4519.767868
For population = 70,000, we predict a profit of 45342.450129
Program paused. Press enter to continue.
Figure 2: Training data with linear regression fit
computeCost 函数
function J = computeCost(X, y, theta)
% 初始化一些值
m = length(y); % 训练集数量
J = 0; % cost
for i = 1:m
J = J + (X(i, :) * theta - y(i))^2;
% X(i, :)表示第i个实例的特征
% hθ(xi) = X(i, :) * theta 第i个实例的预测值
end
J = J / (2 * m); % 输出 theta = [0, 0] 求得的 J 值
end
向量表示求和
function J = computeCost(X, y, theta)
% 初始化一些值
m = length(y); % 训练集数量
E = X * theta - y; % 偏差矩阵
J = (E' * E) / (2 * m); % E' * E 平方和
end
cost function
hypothesis
gradientDescent 函数
function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
% X 样本特征，y 样本实际值，theta 模型参数，alpha 学习率，num_iters 迭代次数
% 初始化一些值
m = length(y);
J_history = zeros(num_iters, 1); % 存储每次迭代的J值
for iter = 1:num_iters % 迭代次数
tmp1 = 0; % 存储求和项
tmp2 = 0;
% 计算求和项
for i = 1:m
tmp1 = tmp1 + (X(i, :) * theta - y(i)); % theta0 对应 X(i, 1) = 1
tmp2 = tmp2 + (X(i, :) * theta - y(i)) * X(i, 2);
end
% 更新 theta
theta(1) = theta(1) - alpha * tmp1 / m;
theta(2) = theta(2) - alpha * tmp2 / m;
% 保存每次迭代的 J 值
J_history(iter) = computeCost(X, y, theta);
end
fprintf('After the last iteration: J = %f\n', J_history(num_iters));
batch gradient descent
J_history
Part 4: Visualizing J(theta_0, theta_1)
To understand the cost function J(θ) better, you will now plot the cost over a
2-dimensional grid of θ0 and θ1 values.（理解为xy平面是theta，z轴是J）
%% ============= Part 4: Visualizing J(theta_0, theta_1) =============
fprintf('Visualizing J(theta_0, theta_1) ...\n')
% 设置计算 J 的网格
theta0_vals = linspace(-10, 10, 100); % 网格范围：-10到10，分成100份
theta1_vals = linspace(-1, 4, 100); % 根据散点图预测 theta 范围
% 初始化 J_vals 存储矩阵：100*100
J_vals = zeros(length(theta0_vals), length(theta1_vals));
% 求 J_vals，1万个(i, j)点，循环体执行1万次
for i = 1:length(theta0_vals)
for j = 1:length(theta1_vals)
t = [theta0_vals(i); theta1_vals(j)]; % 注意 t 是列向量
J_vals(i,j) = computeCost(X, y, t);
end
end
J_vals = J_vals'; % surf 在画 meshgrid 是需要先转置z轴的值
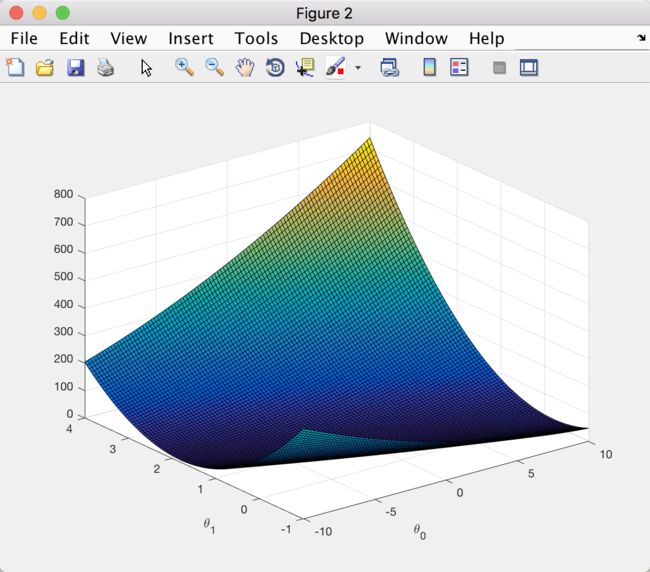
% Surface plot 曲面图
figure; % Figure 2
surf(theta0_vals, theta1_vals, J_vals); % surface 画点
xlabel('\theta_0'); % 坐标轴标签，用 \ 可以转义为字母
ylabel('\theta_1');
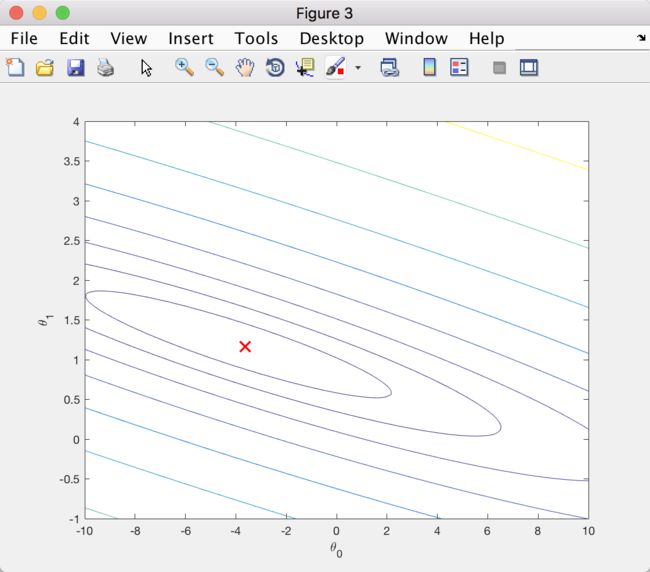
% Contour plot 等值线图
figure; % Figure 3
contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 3, 20)) % 2D 等值线图
% logspace 以 10^x 的形式定义一些列 J 值，x 将[-2, 3]均分为20份
xlabel('\theta_0');
ylabel('\theta_1');
% 在等值线图基础上显示 theta
hold on;
plot(theta(1), theta(2), 'rx', 'MarkerSize', 10, 'LineWidth', 2);
曲面图
等值线图
logspace 实例
y = logspace(-2, 3, 11);
% [-2, 3] 均分为11份，包括端点
% [-2.0, -1.5, -1.0, -0.5, 0, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0]
% 然后 y = power(10, x)
fprintf('%f\n', y) % 向量输出每个元素
