本文主要解答了3个问题,分别是:
1、什么是Gamma值?
2、为什么要进行Gamma校正?
3、如何进行Gamma修校正?
引言
到目前为止,我们渲染的场景看上去还不错。没错,是不错,但是,我们还想把这个场景渲染地更真实更绚丽,该怎么做呢?这时候,我们就需要学习一些更深入入的知识(没错,知识就是力量!)。这章中,我们要讲的知识点就是Gamma校正。
感知亮度与自然亮度
在介绍Gamma之前,先来介绍一下前置知识,这就是感知亮度和自然亮度的区别。什么是自然亮度呢?自然亮度,就是某个物体反射或折射的光子数,光子数越多,亮度就越高。什么是感知亮度呢?就是我感觉这个东西有多量的一种主观感受。但是我们的感觉怎么测量,有什么标准?这些毫无疑问都是没有一定的标准。但是,我们可以通过比较来感知差别。
举了例子:在一个完全封闭的小黑屋中,点亮一支蜡烛A,这只蜡烛对屋内的亮度贡献是显著的。我们可以明显感觉到屋里亮了很多。但如果屋里已经点亮了1000支蜡烛,我再点亮一支蜡烛B的话,我就感觉不出这支蜡烛对屋内的亮度贡献有多少了。这就是感知亮度。而我们可以非常明确的知道,蜡烛A和蜡烛B对贡献的光子数是差不多的,它们提供的自然亮度完全一致。
上图是感知亮度和自然亮度之间的关系。人眼对自然亮度的感知并不是线性的,人眼往往对较暗的部分更敏感,对亮的部分则较为迟钝。这就对我们如何做出符合人眼感知规律的显示提出了挑战!幸运的是,已经有人为我们铺平了道路,我们已经站在了巨人的肩膀上。
Gamma值
说起来Gamma值这东西也真是凑巧,为什么这么说呢,你往下看就知道了。不知道读者中有多少人用过CRT(阴极射线管)显示器?笔者最开始用的电脑配的就是CRT显示器。CRT显示器有一个物理特性就是将输入的电压增大一倍并不会导致亮度也增大一倍。加倍电压会使亮度呈现一个2.2次方的幂指数关系,这个2.2就是显示器的Gamma值。这个值恰好与感知亮度相匹配!
多凑巧的事情!想必造液晶显示器的工程师们不知道耗费了多少脑细胞才找到这个原因。
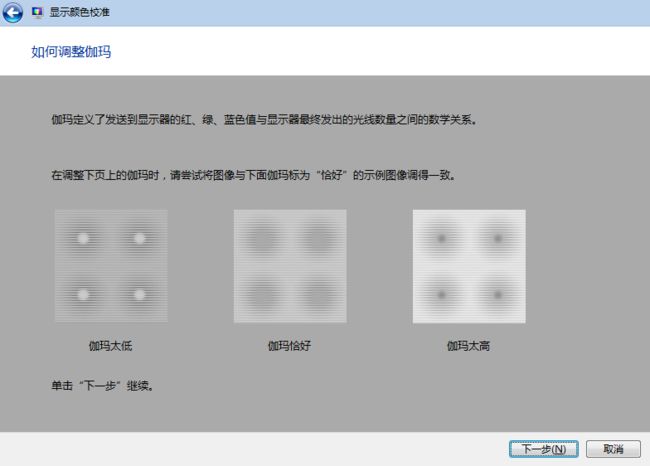
因为人眼对暗的东西更加敏感,所以直到今天,显示器都还有一个Gamma值来重现CRT显示器的自然亮度与感知亮度之间的对应关系。下图是Win7上调整Gamma值时的窗口:
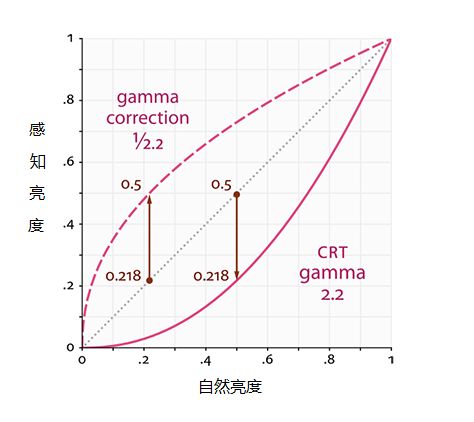
虽然有了Gamma值之后看起来效果更好,但这也让我们产生了困扰:我们是根据从显示器上看到的东西来调整它的颜色和亮度的,但是显示器显示的亮度不是线性的,这怎么处理呢?来看一下下面这张图:
那一条点虚线表示线性空间中的亮度关系(自然亮度=感知亮度)。在它下方的实线表示CRT显示器上自然亮度与感知亮度之间的对应关系(自然亮度50%对应21.8%的感知亮度)。问题来了,如果我现在是在线性空间中操作亮度,我要将0.5的亮度翻一倍变成1.0,但是经过显示器显示后,感知亮度从0.218变成了1.0,亮度就提升了4.5倍。这显然不是我们想要的!
一个解决方法是,我们在计算亮度的时候,先计算亮度的1/2.2次方,让它成为上图中的横虚线,然后再经过显示器的显示时就会变回线性的对应关系,这样我们在控制亮度的时候就比较容易控制了。这种解决方案就是Gamma校正!
Gamma校正
Gamma校正的原理上面已经说了,再重复一遍:由于显示器会对输入的亮度进行一次Gamma幂运算再输出,那么我们在将亮度传输给显示之前,对亮度进行一次逆Gamma幂运算就可以了。还是上面那张图,我们希望直接在中间的线性空间进行操作,当我们想要显示线性空间中的21.8%的亮度时,我们先进行一次逆运算,将其的值变成0.5,然后传递给显示器,显示器进行一次Gamma幂运算之后又将其变成21.8%的亮度进行显示,正好是我们想要的亮度。
将gamma值设置成2.2在大多数显示器上都能有不错的表现。gamma值为2.2的颜色空间称为sRGB颜色空间。每个显示器都会拥有自己的gamma值,所以大部分游戏都允许在游戏内设置自己的Gamma值。(例如星际争霸2里就能设置gamma值)
通常,我们有两种方法来实现gamma校正:
- 使用OpenGL内置的sRGB帧缓存支持
- 在每个片元着色器中都手动进行Gamma校正的计算
前一种的方法简单,但是不够灵活。后一种方法灵活,但是使用起来比较复杂。我们先来看看简单的方法。
调用glEnable(GL_FRAMEBUFFER_SRGB)函数告诉OpenGL之后的绘制操作需要先对颜色进行gamma校正,然后再保存到颜色缓存中。sRGB颜色空间的默认Gamma值为2.2,保证了在大多数机器上显示效果都不错。然后,OpenGL会在执行完片元着色器之后自动进行一次Gamma修正再传入到帧缓存中。这样,最后经过显示器的显示后就是线性空间中的颜色和亮度值了。
比较复杂但是灵活性更高的方法就是我们手动在片元着色器的最后进行一次Gamma校正的运算。记住,Gamma校正的运算必须在片元着色器的末尾运行才正确:
void main()
{
// 渲染操作
...
// 进行Gamma校正
float gamma = 2.2;
FragColor.rgb = pow(fragColor.rgb, vec3(1.0/gamma));
}
最后一行代码就是校正的实际运算操作。
使用手动的方法有一个问题就是你必须在每个片元着色器最后都加上这段校正的代码。如果你有很多片元着色器,那你要加的代码就多了。一个比较简单的方法就是进行一个后期处理的阶段,在将整个场景都渲染完成后进行一次Gamma校正的计算,可以保证场景中的所有物体都执行到了这次计算,而且我们只要进行一次计算就行了,省很多事。
关于Gamma校正的原理和使用方式大概就这些内容,很简单,不过还有一些细节需要考虑。
sRGB纹理
因为显示器在现实的时候总是会应用Gamma值,当你绘制或者编辑一张图片时,你总是基于从显示器上看到的样子。这就意味着你编辑的所有图片都不是基于线性空间而是基于sRGB空间。你觉得把某种颜色调成了2倍的亮度但实际上的数值却没有翻倍。
因为所有人都是基于显示器上看到的样子进行图片绘制合成的,我们在应用中使用图片的时候必须考虑这一点。之前的例子中我们没考虑这一点,因为sRGB空间中的纹理看上去也非常不错,即便没有Gamma校正。因为我们也是在sRGB空间中操作。但现在,我们想在线性空间中操作,将Gamma校正应用之后就出现了亮度太大的问题。
可以很明显地看到,使用了Gamma校正后的显示比原来亮很多,这是因为我们进行了两次Gamma校正的缘故。仔细分析一下,我们做好了一张图片并且在我们的机器上显示的没错,我们就已经校正了一次颜色。然后我们在渲染的时候再校正一次,这样颜色就太亮了。
要解决这个问题,我们有两种方法,其一是确保制作纹理的美术都在线性空间下制作图片。但这方法不太靠谱,因为美术压根儿就不知道显示器有Gamma值,更别提Gamma校正了。
另一个方法是在对sRGB纹理做任何计算之前都将其转换到线性空间中,像这样:
float gamma = 2.2;
vec3 diffuseColor = pow(texture(diffuse, texCoords).rgb, vec3(gamma));
在每个片元着色器中都要这么处理吗?当然不是,OpenGL已经提供了一种更简单的接口来完成这个操作,那就是将纹理的内部格式(internal format)设置成GL_SRGB或者GL_SRGB_ALPHA。
如果我们在创建纹理的时候指定了其中一个参数,那么OpenGL就会自动将颜色转换到线性空间中,我们接下来的操作就都是在线性空间中进行的了。使用的方式如下:
glTexImage2D(GL_TEXTURE_2D, 0, GL_SRGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, image);
还有一点要注意的是并非所有的纹理都是在sRGB空间中的。物体的漫反射纹理通常都是sRGB空间,但是镜面高光纹理和法线贴图一般就已经是在线性空间中了,所以我们在使用的时候还需要多注意不要搞混了才好。
衰减
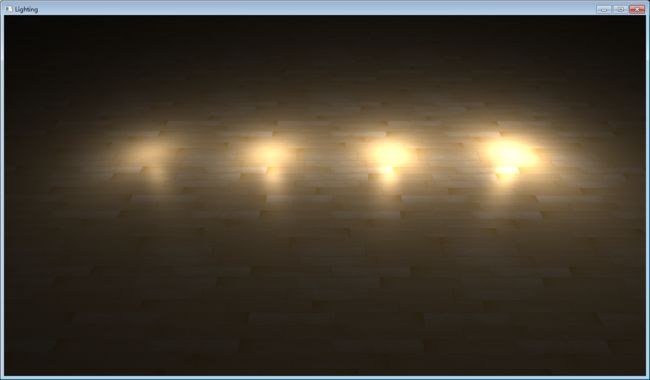
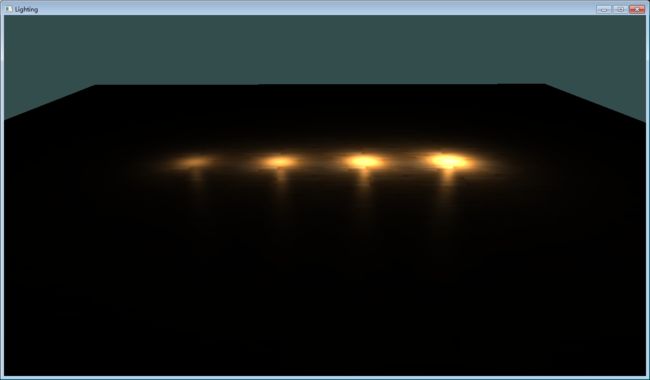
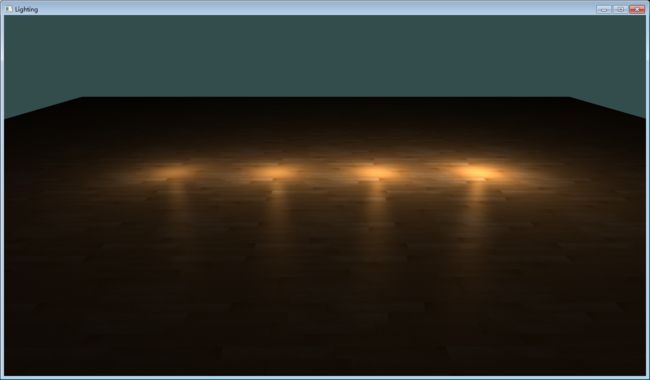
Gamma校正产生的第二个问题就是衰减的计算。之前我们用到的衰减计算是与距离的倒数成正比,因为这样光线不会衰减的过快,看上去更真实。如果用上Gamma校正,那么衰减计算要用与距离平方的倒数成正比才合适,否则会出现场景过亮的问题。对比下面四张图可以看出区别在哪:
产生这种区别的原因,是当我们不使用Gamma校正,使用距离平方的倒数时,衰减的计算就成为这样:(1.0 / (distance ^ 2))^2.2。由于显示器本身的Gamma值关系,亮度衰减会急剧变大,光斑看上去就是非常小的一块。如果使用距离的倒数,衰减的计算就是这样:(1.0 / distance)^2.2 = 1.0 / distance^2.2。这就是正常的衰减公式了。
理解了所有的原理后,下载这里的源码,再回过头去尝试一遍,你就清楚Gamma值和Gamma校正对场景有什么影响了。
总结
本章中,我们学习了显示器Gamma值的由来以及如何进行Gamma校正。从Gamma值的由来,我们学习了更加根本的自然亮度和感知亮度之间的关系。使用Gamma校正也很简单,一个sRGB颜色空间或者是自己手动在片元着色器最后加上校正运算就可以。本文最重要的还是背后的原理,理解了原理,那什么都理解了。
下一篇
目录
下一篇
参考资料
www.learnopengl.com(非常好的网站,建议学习)
en.wikipedia.org/wiki/Gamma_correction(这应该是最权威的解释,没有之一)
www.zhihu.com/question/27467127(这里面的一个高赞回答比较准确而且容易理解)