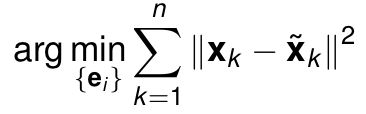- 机器学习与深度学习间关系与区别
ℒℴѵℯ心·动ꦿ໊ོ꫞
人工智能学习深度学习python
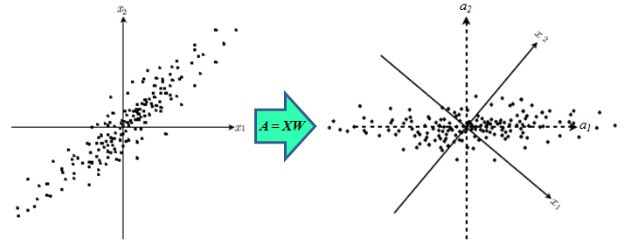
一、机器学习概述定义机器学习(MachineLearning,ML)是一种通过数据驱动的方法,利用统计学和计算算法来训练模型,使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本,识别其中的模式和规律,从而对新的数据进行判断。其核心在于通过训练过程,让模型不断优化和提升其预测准确性。主要类型1.监督学习(SupervisedLearning)监督学习是指在训练数据集中包含输入
- 简单了解 JVM
记得开心一点啊
jvm
目录♫什么是JVM♫JVM的运行流程♫JVM运行时数据区♪虚拟机栈♪本地方法栈♪堆♪程序计数器♪方法区/元数据区♫类加载的过程♫双亲委派模型♫垃圾回收机制♫什么是JVMJVM是JavaVirtualMachine的简称,意为Java虚拟机。虚拟机是指通过软件模拟的具有完整硬件功能的、运行在一个完全隔离的环境中的完整计算机系统(如:JVM、VMwave、VirtualBox)。JVM和其他两个虚拟机
- JVM、JRE和 JDK:理解Java开发的三大核心组件
Y雨何时停T
Javajava
Java是一门跨平台的编程语言,它的成功离不开背后强大的运行环境与开发工具的支持。在Java的生态中,JVM(Java虚拟机)、JRE(Java运行时环境)和JDK(Java开发工具包)是三个至关重要的核心组件。本文将探讨JVM、JDK和JRE的区别,帮助你更好地理解Java的运行机制。1.JVM:Java虚拟机(JavaVirtualMachine)什么是JVM?JVM,即Java虚拟机,是Ja
- 详解“c:/work/src/components/a/b.vue“‘ has no default export报错原因
hw_happy
开发语言前端vue.jsjavascript
前情提要在一个vue文件中需要引入定义的b.vue文件,但是提示b文件没有默认导出,对于vue2文件来说有exportdefault,在中,所有定义的变量、函数和组件都会自动被视为默认导出的组件内容。因此,不需要显式地使用exportdefault来导出组件。但是在我引用这个文件的时候还是提示了这个错误,原来是我的项目使用了ts和vite\webpack,因为TypeScript和Vue的默认导出
- 管理员权限的软件不能开机自启动的解决方法
ss_ctrl
这是几种解决方法:1.将启动参数写入到32位注册表里面去在64位系统下我们64位的程序访问此HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Windows\CurrentVersion\Run注册表路径,是可以正确访问的,32位程序访问此注册表路径时,默认会被系统自动映射到HKEY_LOCAL_MACHINE\SOFTWARE\WOW6432Node\Microsoft
- golang学习笔记--MPG模型
xxzed
golang#学习笔记学习笔记golang
MPG模式:M(Machine):操作系统的主线程P(Processor):协程执行需要的资源(上下文context),可以看作一个局部的调度器,使go代码在一个线程上跑,他是实现从N:1到N:M映射的关键G(Goroutine):协程,有自己的栈。包含指令指针(instructionpointer)和其它信息(正在等待的channel等等),用于调度。一个P下面可以有多个G1、当前程序有三个M,
- 说说在 Vue.js 中如何实现组件间通信
deniro
1用法假设父组件的模板包含子组件,我们可以通过props来正向地把数据从父组件传递给子组件。props可以是字符串数组,也可以是对象。html:js:Vue.component('deniro-component',{props:['message'],template:'{{message}}'});varapp=newVue({el:'#app',data:{}});渲染结果:"嫦娥四号"成功
- java获取applicationcontext,SpringBoot获取ApplicationContext的3种方式
花儿街参考
ApplicationContext是什么?简单来说就是Spring中的容器,可以用来获取容器中的各种bean组件,注册监听事件,加载资源文件等功能。ApplicationContext获取的几种方式1直接使用Autowired注入@ComponentpublicclassBook1{@AutowiredprivateApplicationContextapplicationContext;pub
- Vue组件学习
yancolin
Vue的精华之处就在于它的组件,重复使用,节省代码,提升工作效率。Vue组件要使用先要注册,注册分为全局的和局部的注册。全局注册:注:1.my-component就是注册的组件自定义标签名称;2.template的DOM结构必须被一个元素包含,如果直接写成'全局组件',不带""是无法渲染的。Vue.component('my-component',{template:'全局组件';});varap
- 【开发环境搭建】Macbook M1搭建Java开发环境
weixin_44329069
java开发语言
JDK安装与配置下载并安装JDK:ARM64DMG安装包下载链接:JDK21forMac(ARM64)。双击下载的DMG文件,按照提示安装JDK。配置环境变量:打开终端,使用vim编辑.bash_profile文件:vim~/.bash_profile在文件中添加以下内容来设置JAVA_HOME:exportJAVA_HOME=/Library/Java/JavaVirtualMachines/j
- 机器学习VS深度学习
nfgo
机器学习
机器学习(MachineLearning,ML)和深度学习(DeepLearning,DL)是人工智能(AI)的两个子领域,它们有许多相似之处,但在技术实现和应用范围上也有显著区别。下面从几个方面对两者进行区分:1.概念层面机器学习:是让计算机通过算法从数据中自动学习和改进的技术。它依赖于手动设计的特征和数学模型来进行学习,常用的模型有决策树、支持向量机、线性回归等。深度学习:是机器学习的一个子领
- 联邦学习 Federated learning Google I/O‘19 笔记
努力搬砖的星期五
笔记联邦学习机器学习机器学习tensorflow
FederatedLearning:MachineLearningonDecentralizeddatahttps://www.youtube.com/watch?v=89BGjQYA0uE文章目录FederatedLearning:MachineLearningonDecentralizeddata1.DecentralizeddataEdgedevicesGboard:mobilekeyboa
- CesiumJS+SuperMap3D.js混用实现可视域分析 S3M图层加载 裁剪区域绘制
SteveJi666
WebGLcesiumEarthSDKSuperMap3djavascript前端arcgis
版本简介:cesium:1.99;Supermap3D:SuperMapiClientJavaScript11i(2023);官方下载文档链家:SuperMap技术资源中心|为您提供全面的在线技术服务示例参考:support.supermap.com.cn:8090/webgl/Cesium/examples/webgl/examples.html#analysissupport.supermap
- CesiumJS+SuperMap3D.js混用实现通视分析
SteveJi666
WebGLcesiumEarthSDKSuperMap3djavascript前端arcgis
版本简介:cesium:1.99;Supermap3D:SuperMapiClientJavaScript11i(2023);官方下载文档链家:SuperMap技术资源中心|为您提供全面的在线技术服务示例参考:support.supermap.com.cn:8090/webgl/Cesium/examples/webgl/examples.html#analysissupport.supermap
- Superset二次开发之源码DependencyList.tsx 分析
aimmon
Superset二次开发SupersetBI二次开发typescript前端
功能点路径superset-frontend\src\dashboard\components\nativeFilters\FiltersConfigModal\FiltersConfigForm\DependencyList.tsx/***LicensedtotheApacheSoftwareFoundation(ASF)underone*ormorecontributorlicenseagre
- Android-悬浮窗功能的实现(附Java、KT实现源码)(1)
egrhef
程序员androidjava开发语言
//获取服务的操作对象valbinder=serviceasFloatWinfowServices.MyBinderbinder.service}overridefunonServiceDisconnected(name:ComponentName){}}overridefunonActivityResult(requestCode:Int,resultCode:Int,data:Intent){
- K8S学习笔记02——K8S组件
沉淅尘
#Docker#K8Skubernetes
Kubernetes组件一、控制平面组件(ControlPlaneComponents)(1)kube-apiserver(2)etcd(3)kube-scheduler(4)kube-controller-manager(5)cloud-controller-manager二、Node组件1.kubelet2.kube-proxy3.容器运行时(ContainerRuntime)三、插件(Add
- vue在一个组件引用其他组件
hzw0510
Vuevue.js前端javascript
在vue一个组件中引用另一个组件的步骤必须在script中导入要引用的组件需要在exportdefault的components引用导入的组件(这一步经常忘记)在template使用导入的组件importVue01from"@/components/Vue01.vue";
- 【设计模式】结构型模式:组合模式
KunQAQrz
意图使用组合模式可以将对象组合成树状结构,并且能像使用独立对象一样使用它们。组合模式结构在这里插入图片描述组件(Component)接口描述了树中简单项目和复杂项目所共有的操作。叶节点(Leaf)是树的基本结构,它不包含子项目。一般情况下,叶节点最终会完成大部分的实际工作,因为它们无法将工作指派给其他部分。容器(Container)又名“组合(Composite)”是包含叶节点或其他容器等子项目的
- react中如何获取并使用usestate声明的变量的值
小华0000
react.jsjavascript前端
1.函数式更新当需要根据当前状态来更新状态时,可以使用函数式更新。setState(在类组件中)和setCount(在useState中)都可以接受一个函数作为参数,这个函数接收当前的状态作为参数,并返回新的状态。functionExampleComponent(){const[count,setCount]=useState(0);//使用函数式更新functionhandleClick(){s
- uniapp+uview-plus实现微信小程序自定义tabbar
yx_back
小程序前端uniappuni-app微信小程序uview-plus
参考文档微信小程序相关开发文档链接:https://developers.weixin.qq.com/miniprogram/dev/framework/ability/custom-tabbar.html虽然是uniapp框架但是实现方式和原生小程序相似实现思路1、app.json里面tabBar添加配置custom:true,其他和非自定义设置一样2、在components文件夹里添加Tabb
- Ubuntu虚拟机在node命令行中编译.sol文件报错:{“errors“:[{“component“:“general“,“formattedMessage“...(已解决)
拔牙不打麻药
疑难杂症区块链虚拟机node
Ubuntu虚拟机在node命令行下编译.sol文件报错'{"errors":[{"component":"general","formattedMessage":"*Line1,Column1\\nSyntaxerror:value,objectorarrayexpected.\\n*Line1,Column2\\nExtranon-whitespaceafterJSONvalue.\\n","
- VUE中使用vue-office/pdf预览PDF
人间废料记
vue.jspdf前端
安装npminstall@vue-office/pdfVUE组件中importVueOfficePdffrom'@vue-office/pdf';importEmptyElefrom'@/components/EmptyEle/index';//没有数据时的占位组件constprops=defineProps({pdfUrl:{type:String,default:''}});/*这块是处理边上
- VueTreeselect el-tree-select 多选
小小并不小
Vueelementjsvue.jsjavascript
1、VueTreeselect是一个多选组件npminstall--save@riophae/vue-treeselect全部代码//importthecomponentimportTreeselectfrom'@riophae/vue-treeselect'//importthestylesimport'@riophae/vue-treeselect/dist/vue-treeselect.cs
- Vue 和 React 的对比
淘淘是只狗
vueReactvue.jsreact.jsjavascript
React和Vue有许多相似之处:使用VirtualDOM提供了响应式(Reactive)和组件化(Composable)的视图组件。将注意力集中保持在核心库,而将其他功能如路由和全局状态管理交给相关的库。运行时性能React在React应用中,当某个组件的状态发生变化时,它会以该组件为根,重新渲染整个组件子树。如要避免不必要的子组件的重渲染,你需要在所有可能的地方使用PureComponent,
- 概率潜在语义分析(Probabilistic Latent Semantic Analysis,PLSA)—无监督学习方法、概率模型、生成模型、共现模型、非线性模型、参数化模型、批量学习
剑海风云
ArtificialIntelligence人工智能机器学习概率潜在语义分析PLSA
定义输入:设单词集合为W={ω1,ω2,⋯ ,ωM}W=\{\omega_1,\omega_2,\cdots,\omega_M\}W={ω1,ω2,⋯,ωM},文本集合为D={d1,d2,⋯ ,dN}D=\{d_1,d_2,\cdots,d_N\}D={d1,d2,⋯,dN},话题集合为Z={z1,z2,⋯ ,zN}Z=\{z_1,z_2,\cdots,z_N\}Z={z1,z2,⋯,zN},共现
- echarts象形渐变柱状图
星星跌入梦境*
echartsangular.js前端
一、效果图如下:二、代码如下(1)父组件importitemfrom'../bigdata/components/item.vue'exportdefault{components:{item}}.page-con{width:100%;height:100%;.main-con{width:35%;height:33%;}}(2)子组件importechartsfrom"echarts";exp
- 【Spring】Spring中@Component和@Bean的区别?
九师兄
框架-springbootspringjava后端
1.概述在Spring框架中,@Component和@Bean是两个常用的注解,用于实现组件的声明和配置。它们的主要区别如下:作用对象不同:@Component注解用于声明一个类为Spring容器的组件(Bean),Spring会自动扫描并将其实例化为Bean并管理。@Bean注解用于在配置类(通常是带有@Configuration注解的类)中声明一个方法,该方法的返回值将被注册为Spring容器
- DMA与AXI DMA ip
光之大主宰
FPGAfpga开发硬件架构硬件工程驱动开发
文章目录AXIDMAReadChannel(读通道)WriteChannel(写通道)#其他选项ScatterGatherEngine特点工作流程AXIDMA配置项说明ComponentName(axi_dma)DMA组件的名称,可以自定义。EnableAsynchronousClocks允许DMA在不同时钟域之间工作,适用于不同频率的模块。EnableScatterGatherEngine启用S
- 微信小程序之轮播图组件封装
鱼在在
vueuni-app微信小程序javascript
目录封装组件——mp-rotationchat组件的属性与方法——swiper-rotation-chat.js组件的引入使用封装组件——mp-rotationchat文件目录components(所有组件位置)swiper-roatiton-chat(轮播图组件包)swiper-rotation-chat.wxmlswiper-rotation-chat.jspages(所有页面)index(初
- xml解析
小猪猪08
xml
1、DOM解析的步奏
准备工作:
1.创建DocumentBuilderFactory的对象
2.创建DocumentBuilder对象
3.通过DocumentBuilder对象的parse(String fileName)方法解析xml文件
4.通过Document的getElem
- 每个开发人员都需要了解的一个SQL技巧
brotherlamp
linuxlinux视频linux教程linux自学linux资料
对于数据过滤而言CHECK约束已经算是相当不错了。然而它仍存在一些缺陷,比如说它们是应用到表上面的,但有的时候你可能希望指定一条约束,而它只在特定条件下才生效。
使用SQL标准的WITH CHECK OPTION子句就能完成这点,至少Oracle和SQL Server都实现了这个功能。下面是实现方式:
CREATE TABLE books (
id &
- Quartz——CronTrigger触发器
eksliang
quartzCronTrigger
转载请出自出处:http://eksliang.iteye.com/blog/2208295 一.概述
CronTrigger 能够提供比 SimpleTrigger 更有具体实际意义的调度方案,调度规则基于 Cron 表达式,CronTrigger 支持日历相关的重复时间间隔(比如每月第一个周一执行),而不是简单的周期时间间隔。 二.Cron表达式介绍 1)Cron表达式规则表
Quartz
- Informatica基础
18289753290
InformaticaMonitormanagerworkflowDesigner
1.
1)PowerCenter Designer:设计开发环境,定义源及目标数据结构;设计转换规则,生成ETL映射。
2)Workflow Manager:合理地实现复杂的ETL工作流,基于时间,事件的作业调度
3)Workflow Monitor:监控Workflow和Session运行情况,生成日志和报告
4)Repository Manager:
- linux下为程序创建启动和关闭的的sh文件,scrapyd为例
酷的飞上天空
scrapy
对于一些未提供service管理的程序 每次启动和关闭都要加上全部路径,想到可以做一个简单的启动和关闭控制的文件
下面以scrapy启动server为例,文件名为run.sh:
#端口号,根据此端口号确定PID
PORT=6800
#启动命令所在目录
HOME='/home/jmscra/scrapy/'
#查询出监听了PORT端口
- 人--自私与无私
永夜-极光
今天上毛概课,老师提出一个问题--人是自私的还是无私的,根源是什么?
从客观的角度来看,人有自私的行为,也有无私的
- Ubuntu安装NS-3 环境脚本
随便小屋
ubuntu
将附件下载下来之后解压,将解压后的文件ns3environment.sh复制到下载目录下(其实放在哪里都可以,就是为了和我下面的命令相统一)。输入命令:
sudo ./ns3environment.sh >>result
这样系统就自动安装ns3的环境,运行的结果在result文件中,如果提示
com
- 创业的简单感受
aijuans
创业的简单感受
2009年11月9日我进入a公司实习,2012年4月26日,我离开a公司,开始自己的创业之旅。
今天是2012年5月30日,我忽然很想谈谈自己创业一个月的感受。
当初离开边锋时,我就对自己说:“自己选择的路,就是跪着也要把他走完”,我也做好了心理准备,准备迎接一次次的困难。我这次走出来,不管成败
- 如何经营自己的独立人脉
aoyouzi
如何经营自己的独立人脉
独立人脉不是父母、亲戚的人脉,而是自己主动投入构造的人脉圈。“放长线,钓大鱼”,先行投入才能产生后续产出。 现在几乎做所有的事情都需要人脉。以银行柜员为例,需要拉储户,而其本质就是社会人脉,就是社交!很多人都说,人脉我不行,因为我爸不行、我妈不行、我姨不行、我舅不行……我谁谁谁都不行,怎么能建立人脉?我这里说的人脉,是你的独立人脉。 以一个普通的银行柜员
- JSP基础
百合不是茶
jsp注释隐式对象
1,JSP语句的声明
<%! 声明 %> 声明:这个就是提供java代码声明变量、方法等的场所。
表达式 <%= 表达式 %> 这个相当于赋值,可以在页面上显示表达式的结果,
程序代码段/小型指令 <% 程序代码片段 %>
2,JSP的注释
<!-- -->
- web.xml之session-config、mime-mapping
bijian1013
javaweb.xmlservletsession-configmime-mapping
session-config
1.定义:
<session-config>
<session-timeout>20</session-timeout>
</session-config>
2.作用:用于定义整个WEB站点session的有效期限,单位是分钟。
mime-mapping
1.定义:
<mime-m
- 互联网开放平台(1)
Bill_chen
互联网qq新浪微博百度腾讯
现在各互联网公司都推出了自己的开放平台供用户创造自己的应用,互联网的开放技术欣欣向荣,自己总结如下:
1.淘宝开放平台(TOP)
网址:http://open.taobao.com/
依赖淘宝强大的电子商务数据,将淘宝内部业务数据作为API开放出去,同时将外部ISV的应用引入进来。
目前TOP的三条主线:
TOP访问网站:open.taobao.com
ISV后台:my.open.ta
- 【MongoDB学习笔记九】MongoDB索引
bit1129
mongodb
索引
可以在任意列上建立索引
索引的构造和使用与传统关系型数据库几乎一样,适用于Oracle的索引优化技巧也适用于Mongodb
使用索引可以加快查询,但同时会降低修改,插入等的性能
内嵌文档照样可以建立使用索引
测试数据
var p1 = {
"name":"Jack",
"age&q
- JDBC常用API之外的总结
白糖_
jdbc
做JAVA的人玩JDBC肯定已经很熟练了,像DriverManager、Connection、ResultSet、Statement这些基本类大家肯定很常用啦,我不赘述那些诸如注册JDBC驱动、创建连接、获取数据集的API了,在这我介绍一些写框架时常用的API,大家共同学习吧。
ResultSetMetaData获取ResultSet对象的元数据信息
- apache VelocityEngine使用记录
bozch
VelocityEngine
VelocityEngine是一个模板引擎,能够基于模板生成指定的文件代码。
使用方法如下:
VelocityEngine engine = new VelocityEngine();// 定义模板引擎
Properties properties = new Properties();// 模板引擎属
- 编程之美-快速找出故障机器
bylijinnan
编程之美
package beautyOfCoding;
import java.util.Arrays;
public class TheLostID {
/*编程之美
假设一个机器仅存储一个标号为ID的记录,假设机器总量在10亿以下且ID是小于10亿的整数,假设每份数据保存两个备份,这样就有两个机器存储了同样的数据。
1.假设在某个时间得到一个数据文件ID的列表,是
- 关于Java中redirect与forward的区别
chenbowen00
javaservlet
在Servlet中两种实现:
forward方式:request.getRequestDispatcher(“/somePage.jsp”).forward(request, response);
redirect方式:response.sendRedirect(“/somePage.jsp”);
forward是服务器内部重定向,程序收到请求后重新定向到另一个程序,客户机并不知
- [信号与系统]人体最关键的两个信号节点
comsci
系统
如果把人体看做是一个带生物磁场的导体,那么这个导体有两个很重要的节点,第一个在头部,中医的名称叫做 百汇穴, 另外一个节点在腰部,中医的名称叫做 命门
如果要保护自己的脑部磁场不受到外界有害信号的攻击,最简单的
- oracle 存储过程执行权限
daizj
oracle存储过程权限执行者调用者
在数据库系统中存储过程是必不可少的利器,存储过程是预先编译好的为实现一个复杂功能的一段Sql语句集合。它的优点我就不多说了,说一下我碰到的问题吧。我在项目开发的过程中需要用存储过程来实现一个功能,其中涉及到判断一张表是否已经建立,没有建立就由存储过程来建立这张表。
CREATE OR REPLACE PROCEDURE TestProc
IS
fla
- 为mysql数据库建立索引
dengkane
mysql性能索引
前些时候,一位颇高级的程序员居然问我什么叫做索引,令我感到十分的惊奇,我想这绝不会是沧海一粟,因为有成千上万的开发者(可能大部分是使用MySQL的)都没有受过有关数据库的正规培训,尽管他们都为客户做过一些开发,但却对如何为数据库建立适当的索引所知较少,因此我起了写一篇相关文章的念头。 最普通的情况,是为出现在where子句的字段建一个索引。为方便讲述,我们先建立一个如下的表。
- 学习C语言常见误区 如何看懂一个程序 如何掌握一个程序以及几个小题目示例
dcj3sjt126com
c算法
如果看懂一个程序,分三步
1、流程
2、每个语句的功能
3、试数
如何学习一些小算法的程序
尝试自己去编程解决它,大部分人都自己无法解决
如果解决不了就看答案
关键是把答案看懂,这个是要花很大的精力,也是我们学习的重点
看懂之后尝试自己去修改程序,并且知道修改之后程序的不同输出结果的含义
照着答案去敲
调试错误
- centos6.3安装php5.4报错
dcj3sjt126com
centos6
报错内容如下:
Resolving Dependencies
--> Running transaction check
---> Package php54w.x86_64 0:5.4.38-1.w6 will be installed
--> Processing Dependency: php54w-common(x86-64) = 5.4.38-1.w6 for
- JSONP请求
flyer0126
jsonp
使用jsonp不能发起POST请求。
It is not possible to make a JSONP POST request.
JSONP works by creating a <script> tag that executes Javascript from a different domain; it is not pos
- Spring Security(03)——核心类简介
234390216
Authentication
核心类简介
目录
1.1 Authentication
1.2 SecurityContextHolder
1.3 AuthenticationManager和AuthenticationProvider
1.3.1 &nb
- 在CentOS上部署JAVA服务
java--hhf
javajdkcentosJava服务
本文将介绍如何在CentOS上运行Java Web服务,其中将包括如何搭建JAVA运行环境、如何开启端口号、如何使得服务在命令执行窗口关闭后依旧运行
第一步:卸载旧Linux自带的JDK
①查看本机JDK版本
java -version
结果如下
java version "1.6.0"
- oracle、sqlserver、mysql常用函数对比[to_char、to_number、to_date]
ldzyz007
oraclemysqlSQL Server
oracle &n
- 记Protocol Oriented Programming in Swift of WWDC 2015
ningandjin
protocolWWDC 2015Swift2.0
其实最先朋友让我就这个题目写篇文章的时候,我是拒绝的,因为觉得苹果就是在炒冷饭, 把已经流行了数十年的OOP中的“面向接口编程”还拿来讲,看完整个Session之后呢,虽然还是觉得在炒冷饭,但是毕竟还是加了蛋的,有些东西还是值得说说的。
通常谈到面向接口编程,其主要作用是把系统��设计和具体实现分离开,让系统的每个部分都可以在不影响别的部分的情况下,改变自身的具体实现。接口的设计就反映了系统
- 搭建 CentOS 6 服务器(15) - Keepalived、HAProxy、LVS
rensanning
keepalived
(一)Keepalived
(1)安装
# cd /usr/local/src
# wget http://www.keepalived.org/software/keepalived-1.2.15.tar.gz
# tar zxvf keepalived-1.2.15.tar.gz
# cd keepalived-1.2.15
# ./configure
# make &a
- ORACLE数据库SCN和时间的互相转换
tomcat_oracle
oraclesql
SCN(System Change Number 简称 SCN)是当Oracle数据库更新后,由DBMS自动维护去累积递增的一个数字,可以理解成ORACLE数据库的时间戳,从ORACLE 10G开始,提供了函数可以实现SCN和时间进行相互转换;
用途:在进行数据库的还原和利用数据库的闪回功能时,进行SCN和时间的转换就变的非常必要了;
操作方法: 1、通过dbms_f
- Spring MVC 方法注解拦截器
xp9802
spring mvc
应用场景,在方法级别对本次调用进行鉴权,如api接口中有个用户唯一标示accessToken,对于有accessToken的每次请求可以在方法加一个拦截器,获得本次请求的用户,存放到request或者session域。
python中,之前在python flask中可以使用装饰器来对方法进行预处理,进行权限处理
先看一个实例,使用@access_required拦截:
?