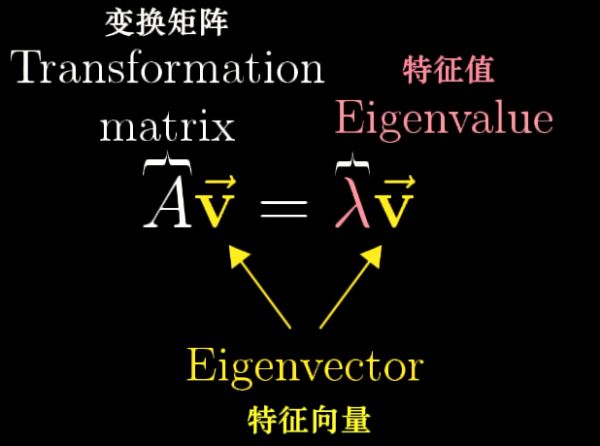
“特征”一词译自德语的eigen, 意味着“自身的”,“有特征的” — 这强调了特征值对于定义特定的线性变换上是很重要的.
☺特征值 / 特征向量
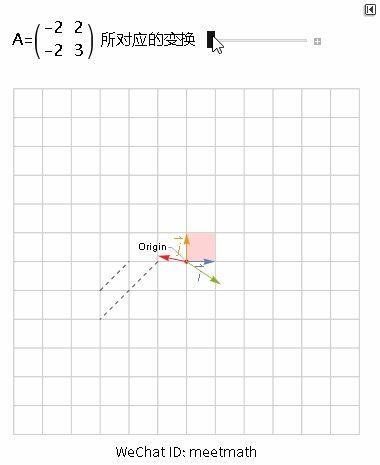
我们来观察在矩阵 A 的作用下空间发生的线性变换, 注意下图中红色向量和绿色向量的变化:
观察要点:
- 空间发生了倾斜, 但(黑色虚线)直线还是直线, 依然保持平行(线性性质);
- 变换过程中发生了镜像翻转, 所以行列式为负值 -2;
- 基向量 i 变换到 (-2,-2) 处, 基向量 j 变换到 (2,3) 处;
- 红绿两个向量都随之发生了旋转;
是不是空间中所有的向量都会进行旋转呢? 还是这个矩阵变换为例, 再来观察下面这 3 个向量.
观察要点:
- 红绿 3 个向量的长度发生了伸缩变换, 但仍在原来的直线方向上, 并未发生旋转;
- 两条直线上的任何其他向量都只是被拉伸为原来的 2 倍和 -1 倍, 如红色两个向量都伸长为 2 倍;
- 除了这两条直线外, 空间中的其他向量在变换过程中都有旋转(见上图);
这里只有长度伸缩起了变化, 而方向仍在原直线上的向量就是矩阵 A 的特征向量(Eigenvectors. 伸缩的倍数, 就是特征值(Eigenvalues), 红色向量 (1,2) 伸长了 2 倍, 特征值为 2; 绿色向量 (2,1) 伸缩倍率为 -1, 相应特征值为 -1.
一般而言, 对于 nxn 方阵 A , 当存在向量 v 不是零向量, 且满足
等号左边是矩阵向量的乘积, 而右边是数乘向量.
☺特征值的计算
如何求解出特征值呢, 考虑将上面等式右边项移项:
我们知道只有当 (A-λ I) 这个矩阵所代表的变换是压缩扁平化操作的时候才会将向量 v 压缩至原点处, 而压缩扁平化的矩阵的行列式应该等于 0 , 这样只需要求解出相应的特征方程即可得到 λ 的结果.
一旦求出了矩阵的特征值, 之后要做的就是带入定义式子, 求出满足定义的特征向量了.
❥ 部分截图出自 3Blue1Brown 的《线性代数 的本质》视频;
❥ 视频可以从 YouTube 或 B站搜索3Blue1Brown 在线观看, 或者在[遇见数学]公众号号后台, 分别输入关键字[高等数学]和[线性代数]直接得到下载地址.
上面就是本次图解线性代数所回顾的知识点. 好了, 现在让我们在下一篇的中再见!
因为本人水平有限, 疏忽错误在所难免, 还请各位老师和朋友多提宝贵意见, 帮助我改进这个系列, 您的关注和转发就是鼓励我继续前行的最大动力, 感谢感谢!