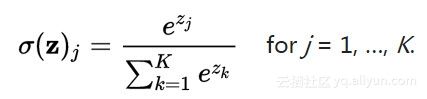系列文章:
一入侯门“深”似海,深度学习深几许(深度学习入门系列之一)
人工“碳”索意犹尽,智能“硅”来未可知(深度学习入门系列之二)
神经网络不胜语, M-P模型似可寻(深度学习入门系列之三)
“机器学习”三重门,“中庸之道”趋若人(深度学习入门系列之四)
深度学习入门系列,用白话文的方式让你看得懂学的快(第五章)
损失函数减肥用,神经网络调权重(深度学习入门系列之六)
山重水复疑无路,最快下降问梯度(深度学习入门系列之七)
深度学习入门系列,用白话文的方式让你看得懂学的快(第八章)
全面连接困何处,卷积网络见解深(深度学习入门系列之九)
卷地风来忽吹散,积得飘零美如画(深度学习入门系列之十)
局部连接来减参,权值共享肩并肩(深度学习入门系列之十一)
摘要:斑点的青蛙为何会被视为异类,四脚的壁虎又为何被视为同族?它们背后隐藏着怎样的“机器学习”原理?它们的关系是如何曲折“激活”这一系列复杂矛盾的?它们又是如何“池化”特征,“全连接”彼此,以便达到“各回各家,各找各妈”的分类?敬请关注本节关于激活层,池化层及全连接层的相关内容。
12.1 两个看似闲扯的问题
在开讲本章内容之前,先请你思考两个问题呗:第一个问题,你能用直线画出一张漂亮的笑脸吗?第二个问题是,你知道那副著名的对联:“诸葛一生唯谨慎,吕端大事不糊涂”,说得是什么典故吗?
如果你不是抬杠的话,我想你第一个问题的答案,应该是不能。因为直线的表现力非常有限,只有曲线才能画出更美的线条。因此,才有英国画家和美学家威廉•荷加兹(William Hogarth,1697~1764)这个的结论:“世界上最美的线条是曲线”。
第二问题说的是,诸葛当然是指“诸葛亮”。其人掌军理政之谨慎,史家已有共识。但过于谨慎是有代价的,那就是面临新情况做决策时,考虑因素过多,思前顾后,从而使其判断力(或称之为预测力)大打折扣。而同样身居高位的吕端则不同。吕端是宋朝一个名宰相,别看他平时是糊里糊涂的,很多鸡零狗碎之事,他从不斤斤计较。但一旦涉及原则性、重要关键决策点时,吕端从不马虎,其风格有点像“大行不顾细谨”。
12.2 追寻问题的本质
前面我们提了两个问题,看似闲扯,其实不然。因为它们的答案都和今天的主题相关。问题一的答案其实是想说明一个结论,就是线性的事物,表达能力不强,而非线性则相反。我们知道,从宏观来将,在本质上,人工神经网络就分为两大类层:显层和隐层。“显层”就是我们能感知到的输入层和输出层,而“隐层”则是除了输入输出之外的无法被我们感知的层,它可以理解为数据的内在表达[1]。
在第二章中,我们已经提到,如果“隐层”有足够多的神经元,那么神经网络能够以任意精度逼近任意复杂度的连续函数,这就是大名鼎鼎的通用近似定理(Universal Approximation Theorem)[2]。通过在第八章BP算法的讲解中,我们可以看到,神经元与神经元的连接都是基于权值的线性组合。我们知道,线性的组合依然是线性的,那网络的表达能力就非常有限了。这样一来,通用近似定理又是如何起作用的呢?这就得请“激活”函数出马了?神经元之间的连接是线性的,但激活函数可不一定是线性的啊,有了非线性的激活层在,多么玄妙的函数,我们都能近似表征出来。所以,在卷积神经网络中,激活层是必须保留的。
第二个问题的答案,其实是想说明深度学习训练的两大难点:过拟合(overfitting)和欠拟合(underfitting)。那什么是过拟合和欠拟合呢?图12-2可形象地说明这两个概念的差别。
“欠拟合”比较容易理解,就是样本不够,或学习算法不精,连已有数据中的特征都没有学习好,自然当面对新样本做预测时,效果肯定也好不到哪里去。比如说,在图12-2中(右下图),若果仅仅把样本中的“四条腿”当作青蛙的特征,这“欠缺”的特征,就会把一只四条腿的壁虎也当作青蛙。其实,欠拟合比较容易克服,比如在决策树算法中扩展分枝,再比如在神经网络中增加训练的轮数,从而可以更加“细腻”地学习样本种的特征。
相比而言,要克服过拟合,就相对困难得多。在过拟合里,构建的模型必须一丝不苟地反映已知的所有数据,但这样一来,它对未知数据(新样本)的预测能力就会比较差。
这是因为,所谓的“已知”数据,其实也是有误差的!精准的拟合会把这些数据的误差给放大。从而导致,拟合得越精确,面对新样本时,预测的效果反而会更加糟糕。比如说图12-2中(右上图),误把背上斑点当做青蛙的特征,当新来的样本青蛙,仅仅由于背上没有斑点(不同于样本数据),就被判定为非青蛙,这岂不是很荒诞?“诸葛一生唯谨慎”,说的就是诸葛亮陷入“过拟合”状态,他容易被很多细节所迷惑,自然决策的质量就会受到影响。
“吕端大事不糊涂”说的就是,小事情上“难得糊涂”,大事情上“毫不含糊”。遇到新情况,吕端就不会受很多细节所左右。用机器学习的术语来讲,吕端的“泛化能力”比较强。
卷积神经网络也追求泛化(即防过拟合)能力,它是如何做到的呢?自然也得学习“吕端”的行为——别管那么多!
针对神经网络,就是再次降低数据量,让系统少学点。不要认为,训练数据越“全面”越好。想一想人类的学习就知道怎么回事了。当孩子还小正处于学习阶段时,妈妈们的浓浓爱意,总想通过“事无巨细”地照顾孩子表达出来。但在这种环境下“学习”出来的孩子,一旦踏上社会,适应新环境的能力就差很多,并不值得提倡。神经网络也是如此。
那该如何降低数据量呢?最简单的策略自然就是“采样(sampling)”了。其实,采样的本质就是力图以合理的方式“以偏概全”。这样一来,数据量自然就降低了。
在卷积神经网络中,采样是针对若干个相邻的神经元而言的,因此也称为“亚采样(Subsampling)”。可能是“亚采样”这个词的逼格不够高吧,于是研究者们又给它取了个更难懂的词:“池化(Pooling)”。“池化”其实仅仅是个字面的翻译,远没达不到“信达雅”的要求,如果非要向“采样”的含义靠拢,中国那句古话,“弱水三千只取一瓢”,似乎更有韵味。南京大学周志华老师就将其的意译为“汇合”,这样的翻译似乎更加传神。但拗不过太多人都把“Pooling”翻译成“池化”,那我们也就“池化”叫下去吧。
接下来,我们就详细说一说激活层和池化层到底是怎么回事吧。
12.3 细说激活层
通过前面的铺垫,现在我们应该知道,激活层存在的最大目的,莫过于引入非线性因素,以增加整个网络的表征能力。
这时,选取合适的“激活函数”就显得非常重要了。在前面的章节中,我们提到了常用的激活函数Sigmoid(或tanh函数),也是可用的(如图12-3所示)。
但Sigmoid之类激活函数有个很大的缺点,就是它的导数值很小。比如说,Sigmoid的导数取值范围仅为[0, 1/4]。且当输入数据(x)很大或者很小的时候,其导数趋都近于0。这就意味着,很容易产生所谓的梯度消失(vanishing gradient)现象。没有了梯度的指导,那么神经网络的参数训练,就如同“无头的苍蝇”,毫无方向感。
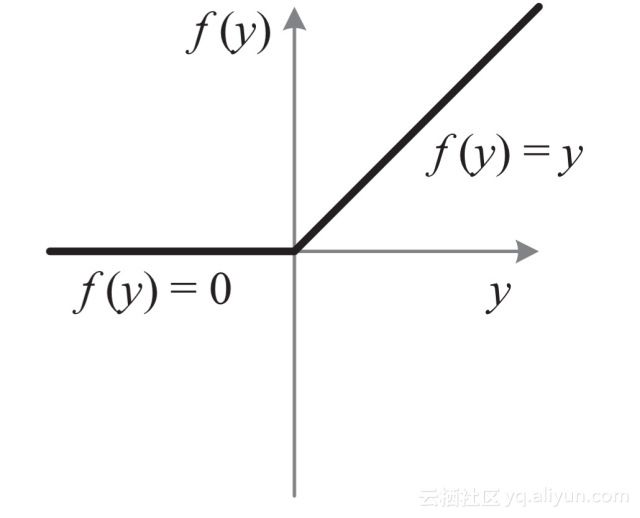
因此,如何防止深度神经网络陷入梯度消失,或说如何提升网络的训练效率,一直都是深度学习非常热门的研究课题。目前,在卷积神经网络中,最常用的激活函数久是修正线性单元(Rectified Linear Unit,简称ReLU)。这个激活函数是由Hinton等人2010年提出来的[3]。标准的ReLU函数为f(x)=max(x,0),即当x>0时,输出x;当x<=0时,输出0。如图12-4所示,请注意,这是一条曲线啊,只不过它在原点处不够那么圆润而已。
不要小看这个看起来有点简陋的模型,其实它的优点还不少。相比于Sigmoid类激活函数,ReLU激活函数的优点主要体现在如下三点。
(1)单侧抑制。观察图12-4可见,当输入小于0时,神经元处于抑制状态。反之,当输入大于0,神经元处于激活状态。
(2)相对宽阔的兴奋边界。观察图12-3和图12-4可见,Sigmoid的激活态(即f(x)的取值)集中在中间的狭小空间,而ReLU这不同,只要输入大于0,神经元一直都处于激活状态。
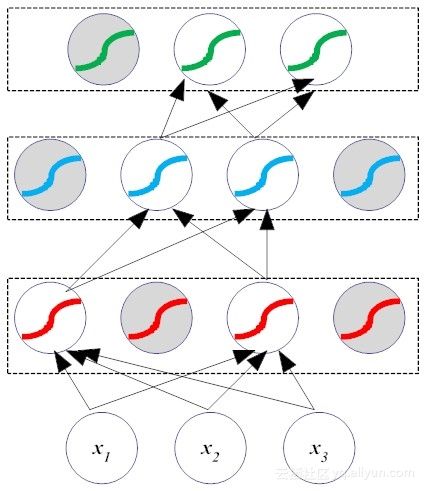
(3)稀疏激活性。相比于Sigmoid之类的激活函数,稀疏性是ReLU的优势所在[4]。Sigmoid把抑制状态的神经元设置一个非常小的值,但即使这个值再小,后续的计算还少不了它们的参与,计算负担很大。但考察图12-4可知,ReLU直接把抑制态的神经元“简单粗暴”地设置为0,这样一来,就使得这些神经元不再参与后续的计算,从而造成网络的稀疏性,如图12-5所示。
这个细小的变化,让ReLU在实际应用中大放异彩,除了减少了计算量,还减少了参数的相互依存关系(网络瘦身了不少),使其收敛速度远远快于其他激活函数,最后还在一定程度上缓解了过拟合问题的发生(对Dropout机制比较熟悉的读者可能会发现,图12-5和Dropout的迭代过程何其神似!)。ReLU的卓越表现,让深度学习的三位大咖Yann LeCun、Yoshua Bengio和Geoffery Hinton在2015年表示,ReLU是深度学习领域最受欢迎的激活函数。
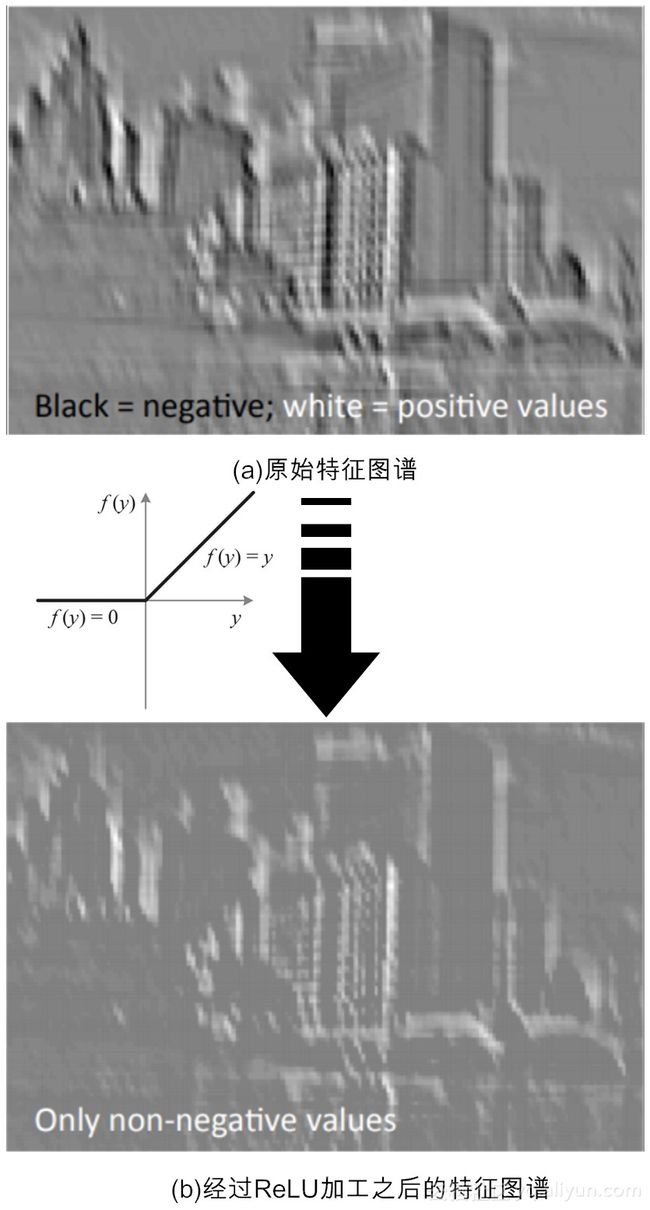
前面的描述可能还过于抽象,下面我们再用一个更为生动的案例来理解ReLU的操作,图12-6演示了ReLU“修正”前后的特征图谱。
说到ReLU激活函数有如此神奇作用,其实还有一个原因,那就是这样的模型正好“暗合”生物神经网络工作机理。2003年纽约大学教授Peter Lennie的研究发现[5],大脑同时被激活的神经元只有1~4%,即神经元同时只对输入信号的少部分选择性响应,大量信号被刻意地屏蔽了,这进一步表明神经元工作的稀疏性。其实,这是容易理解的,因为生物运算也是需要成本的。进化论告诉我们,作为人体最为耗能的器官,大脑尽要可能节能,才能在恶劣的环境中“适者生存”。
当然,LeRU的这种简单直接的处理方式,也带来一些副作用。最突出的问题就是,会导致网络在训练后期表现得非常脆弱,以至于这时的ReLU也被戏称为“死掉的ReLU(dying ReLU)”。目前,也有一些对研究工作对ReLU实施改进,分别提出了一系列诸如leaky-ReLU,random ReLU及PReLU[6]等优化方案,有兴趣的读者可自行前往查阅相关文献。
前面说完了激活层,下面我们再聊聊池化层。
12.4 详解池化层
池化层亦称子采样层,它也是卷积神经网络的另外一个“神来之笔”。通常来说,当卷积层提取目标的某个特征之后,我们都要在两个相邻的卷积层之间安排一个池化层。
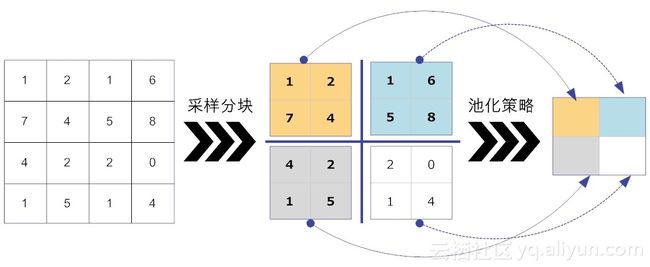
池化层函数实际上是一个统计函数。以如图12-7所示的二维数据为例,如果输入数据的维度大小为W×H,给定一个池化过滤器,其大小为w×h。池化函数考察的是在输入数据中,大小为w×h的子区域之内,所有元素具有的某一种特性。常见的统计特性包括最大值、均值、累加和及L2范数等。池化层函数力图用统计特性反应出来的1个值,来代替原来w×h的整个子区域。
因此,可以这么说,池化层设计的目的主要有两个。最直接的目的,就是降低了下一层待处理的数据量。比如说,当卷积层的输出大小是32×32时,如果池化层过滤器的大小为2×2时,那么经过池化层处理后,输出数据的大小为16×16,也就是说现有的数据量一下子减少到池化前的1/4。当池化层最直接的目的达到了,那么它的间接目的也达到了:减少了参数数量,从而可以预防网络过拟合。
下面我们举例说明常用的池化策略最大化和平均化是如何工作的。我们以一维向量数据[1, 2, 3, 2]为例,来说明两种不同的池化策略在正向传播和方向传播中的差异[7]。
(1)最大池化函数(max pooling)
前向传播操作:取滤波器最大值作为输出结果,因此有forward(1, 2, 3, 2) = 3.
反向传播操作:滤波器的最大值不变,其余元素置0。因此有backward(3) = [0, 0, 3, 0]。
(2)平均池化函数(average pooling)
前向传播操作:取滤波器范围所有元素的平均值作为数据结果,因此有forward(1, 2, 3, 2) = 2.
后向传播操作:滤波器中所有元素的值,都取平均值,因此有backward(2) = [2, 2, 2, 2]。
有了上面的解释,我们很容易得出图12-7中所示的池化策略前向传播结果,如图12-8所示。
阅读到此,读者可能会有个疑问?对于处理图片而言,如果池化层的过滤器2×2,就相当于将上一层4个像素合并到一个1像素。如果过滤器的大小是6×6,那就相当于将上一层36个像素合并到一个1像素,这也岂不是让图像更加模糊了。的确是这样,通过池化操作后,原始图像就好像被打上了一层马赛克,如图12-9所示。对池化如何影响可视化图像的理论分析,感兴趣的读者可参阅LeCun团队的论文[8]。
图12-9给出了池化之后的“马赛克”类的图片,很显然,人类是不喜欢这样模糊图片的。但请注意,计算机的“视界”和人类完全不同,池化后的图片,丝毫不会影响它们对图片的特征提取。
这么说是有理论支撑的。这个理论就是局部线性变换的不变性(invariant)。它说的是,如果输入数据的局部进行了线性变换操作(如平移或旋转等),那么经过池化操作后,输出的结果并不会发生变化。局部平移“不变性”特别有用,尤其是我们关心某个特征是否出现,而不关心它出现的位置时。例如,在模式识别场景中,当我们检测人脸时,我们只关心图像中是否具备人脸的特征,而并不关心人脸是在图像的左上角和右下角。
因为池化综合了(过滤核范围内的)全部邻居的反馈,即通过k个像素的统计特性而不是单个像素来提取特征,自然这种方法能够大大提高神经网络的性能[9]。
12.5 勿忘全连接层
前面我们讲解了卷积层、激活层和池化层。但别忘了,在卷积神经网络的最后,还有一个至关重要的“全连接层(Fully Connected Layer,简称FC)”。“全连接”意味着,前层网络中的所有神经元都与下一层的所有神经元连接。全连接层设计目的在于,它将前面各个层学习到的“分布式特征表示”,映射到样本标记空间,然后利用损失函数来调控学习过程,最后给出对象的分类预测。
实际上,全连接层是就是传统的多层感知器(类似于我们在第八章学过的BP网络,不熟悉的读者可以前往查阅)。不同于BP全连接网络的是,卷积神经网络在输出层使用的激活函数不同,比如说它可能会使用Softmax函数。
这里,我们简单介绍一下这个Softmax函数。在数学上,Softmax函数又称归一化指数函数,它是逻辑函数的一种推广,其公式如(12-2)所示。
我们常用SVM(支持向量机)来做分类器,SVM在分类的最后,会给一系列的标签如“猫”“狗”“船”等打一个具体分值,如[4, 1, -2],而Softmax函数有所不同,它把这些分值实施规则化(regularization),也就是说,将这些实分值转换为一系列的概率值(信任度),如[0.95, 0.04, 0.0],如图12-10所示。由此可见,其实SVM和Softmax是高度相互兼容的,不过是表现形式不同而已。
虽然全连接层处于卷积神经网络最末的位置,看起来貌不惊人似的,但由于全连接层的参数冗余,导致该层的参数个数占据整个网络参数的绝大部分。这样一来,稍有不慎,全连接层就容易陷入过拟合的窘境,导致网络的泛化能力难尽人意。
12.7 小结与思考
到此为止,我们介绍完毕了卷积神经网络的所有核心层。各个层各司其职,概括起来,卷积层从数据中提取有用的特征;激活层为网络中引入非线性,增强网络表征能力;池化层通过采样减少特征维度,并保持这些特征具有某种程度上的尺度变化不变性。在全连接层实施对象的分类预测。
通过上面的学习,请你思考如下问题。
(1)由于全连接层因为参数个数太多,容易出现过拟合的现象,你知道Hinton教授的团队是采取的是什么措施来弱化这样现象吗?(提示:Dropout)
(2)全连接层的性能不甚如人意,很多研究人员做了改进。比如,现任360公司首席科学家颜水成博士团队曾发表了论文“网中网(Network In Network,NIN)[10]”。文中提出了用全局均值池化策略(Global Average Pooling,GAP),取代全连接层,你知道它的工作原理是什么吗?
此外,向推荐读者学习李飞飞(Feifei Li)教授团队在斯坦福大学开设的公开课:面向可视化识别的卷积神经网络(CS231n: Convolutional Neural Networks for Visual Recognition),课程极其精彩。毫不夸张地说,比Ian Goodfellow等人所著的《深度学习》可读性要高很多[9]。
写下你的感悟,祝你每天都有收获。
参考文献
[1] 周志华.机器学习.清华大学出版社.2016.1
[2] Hornik K, Stinchcombe M, White H. Multilayer feedforward networks are universal approximators[J]. Neural networks, 1989, 2(5): 359-366.
[3] Nair V, Hinton G E. Rectified linear units improve restricted boltzmann machines[C]// International Conference on International Conference on Machine Learning. Omnipress, 2010:807-814.
[4] Glorot X, Bordes A, Bengio Y. Deep Sparse Rectifier Neural Networks[C]// International Conference on Artificial Intelligence and Statistics. 2011.
[5] Lennie P. The Cost of Cortical Computation[J]. Current Biology Cb, 2003, 13(6):493-7.
[6] He K, Zhang X, Ren S, et al. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification[C]// IEEE International Conference on Computer Vision. IEEE, 2015:1026-1034.
[7] 黄安埠. 深入浅出深度学习.中国工信出版社.2017.6
[8] Boureau Y L, Ponce J, Lecun Y. A Theoretical Analysis of Feature Pooling in Visual Recognition[C]// International Conference on Machine Learning. DBLP, 2010:111-118.
[9] Ian Goodfellow, Yoshua Bengio, Aaron Courville. 深度学习.人民邮电出版社。 2017.8
[10]Lin M, Chen Q, Yan S. Network In Network[J]. Computer Science, 2013.
文章作者:张玉宏,著有《品味大数据》一书。审校:我是主题曲哥哥。
(未完待续)