现在有一批家庭用电情况的数据,对数据进行算法模型预测,并最终得到预测模型(每天各个时间段和功率之间的关系、功率和电流之间的关系等)
数据来源:
建议:使用python的sklearn库的linear_model中的LinearRegression来获取算法
1、头文件:
##家庭用电预测:线性回归算法(时间与功率&功率与电流之间的关系)
## 一般用到sklearn的子库
import sklearn
#训练集测试集划分,最新版本中该库直接归到了sklearn的子库
from sklearn.model_selection import train_test_split
# 线性模型
from sklearn.linear_model import LinearRegression
# 预处理的库
from sklearn.preprocessing import StandardScaler
## 再提一下标准化的概念:
## StandardScaler作用:去均值和方差归一化
## 假如对于某个特征中的一列数据集,x1,x2, ... ,xn
## 标准化后的数据: (x1-均值)/标准差,(x2-均值)/标准差, ... ,(xn-均值)/标准差
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
import time
2、 设置字符集,防止中文乱码
mpl.rcParams['font.sans-serif'] = ['simHei']
mpl.rcParams['axes.unicode_minus'] = False
3、 加载数据
## 日期、时间、功率1、功率2、电压、电流、厨房用电功率、洗衣用电功率、热水器用电用率
## 数据文件的路径
path1 = 'C:\\Users\\Gorde\\Desktop\\household_power_consumption\\household_power_consumption_100.txt'
#如果没有混合类型的数据时,可以通过low_memory=False来调用更多的内存,提高读取速度
df = pd.read_csv(path1,sep=';',low_memory=False)
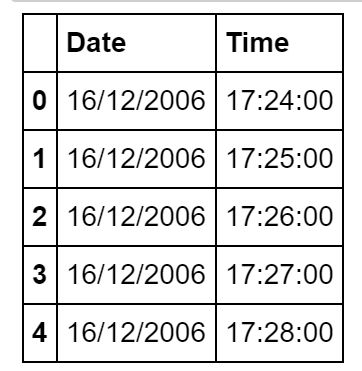
df.head() # 获取前五行
df.tail() #获取后五行
4、 处理异常数据
new_df = df.replace('?',np.nan) #替换非法字符为nan空
## how='any' 遇到空值就删掉; axis=0 删除行;
data = new_df.dropna(axis=0,how='any')
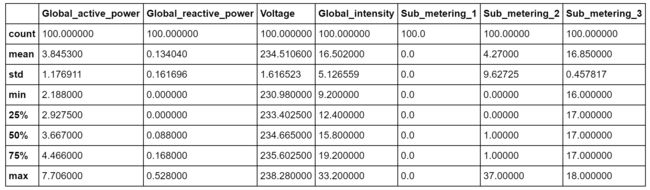
5、 查看整个数据集的构成,以及数据的大致分布。
## count一共多少条数据; mean均值; std标准差; min最小值 ;man最大值;
## 25% 四分之一分位数; 50% 二分之一分位数; 75% 四分之三分位数;
data.describe()
=== 构建的模型的需求 ===
家庭用电预测:线性回归算法(时间与功率&功率与电流之间的关系)
要计算时间和功率的关系,那么应该去看一看时间的数据格式是什么。
创建一个关于时间的格式化字符串函数:
##时间 16/12/2006 用 %d/%m/%Y %H:%M:%S 格式化的方法处理数据
def data_fromat(dt):
t = time.strptime(' '.join(dt),'%d/%m/%Y %H:%M:%S')
return (t.tm_year,t.tm_mon,t.tm_mday,t.tm_hour,t.tm_min,t.tm_sec)
解释下join函数
data_fromat函数中传入的参数dt,是包含了(Date,Time)两个字符串的元组,用空格隔开。
str = " ";
dt1 = ("16/12/2006", "18:59:00"); # 字符串序列
str.join( dt1 )
'16/12/2006 18:59:00'
6、 获取x和y变量,并将时间转化为数值型的连续变量
首先回顾一下数据:
data.head()
获取所有行的前两列:
X = data.iloc[:,0:2]
X.head()
#X = X.apply(lambda x:pd.Series(data_fromat(x)),axis=1)
对X中的所有列作data_fromat操作:
## 其中axis=1 传入 data_fromat的 x=(16/12/2006,17:24:00);
## 其中axis=0 传入 data_fromat的 x=(16/12/2006,16/12/2006, ... ,16/12/2006);
## 根据axis=1 运算,每次从data_fromat返回的元组转化成新的矩阵行
## 原本100行[Date,Time]的矩阵,重构成100行的[年,月,日,时,分,秒]的矩阵
X = X.apply(lambda x:pd.Series(data_fromat(x)),axis=1)
X.head()
请结合data_fromat关于时间的格式化字符串函数,再次回顾上面的操作
def data_fromat(dt):
t = time.strptime(' '.join(dt),'%d/%m/%Y %H:%M:%S')
return (t.tm_year,t.tm_mon,t.tm_mday,t.tm_hour,t.tm_min,t.tm_sec)
7、 要计算时间和功率的关系
之前已经获取到了时间的矩阵 (将时间转化为数值型的连续变量)
现在要获取时间矩阵对应的功率。
获取时间对应的 "功率1" 的值 Global_active_power;
即获取x和y变量
构建 [目标值|样本] =》[Y|X] ;
Y = data['Global_active_power']
Y.head()
8、 测试集、训练集划分
上面完成了对总数据data "竖着切" 的过程
即,将(目标-功率)和(特征-时间)抽取出来) 形成了[Y|X]
现在要对100行[Y|X]数据 "横着切" (构建训练集和测试集)
对数据集进行测试集训练集的划分
test_size=0.2 说明训练集80条,测试集20条,测试集占20%
X_train,X_test,Y_train,Y_test = train_test_split(X,Y,test_size=0.2,random_state=0)
训练集:X的数据类型和数量
print(type(X_train))
print(len(X_train))
X_train.head(2)
测试集:Y的数据类型和数量
print(type(Y_test))
print(len(Y_test))
print('-'*40)
Y_test.head(2)
9、观测数据标准化
## StandardScaler 画图纸
ss = StandardScaler()
## fit_transform训练并转换
## fit在计算,transform完成输出
X_train = ss.fit_transform(X_train)
X_train
这步操作是很多人不理解的地方。
首先观测一下X_train数组的值,
我们发现这是一个array类型,值在0的左右徘徊。
[0.,0.,0.,0.50260283,-1.36580168,0.],[0.,0.,0.,0.50260283, -0.27027738,0.],...
StandardScaler 在sklearn中也称为转换器(有输入数据,有输出数据)
现在我们画了一张图纸,ss = StandardScaler() ;
图纸ss表示:我要用StandardScaler这个方法对数据进行标准化。
将数据放入图纸: Data->ss ,将数据放入图纸后,图纸中的转换器开始运算。
转化器运算什么?
首先对于Data每一列特征的均值和方差进行计算,得到[μ1~μn] 和 [σ1~σn] ;
根据旧的Data,逐一计算每个特征的 (x-μ)/σ,并构成新的 Data
最后获得的新Data就是数据标准化的结果。
fit的操作完成了以上的计算工作;
transform完成了对新Data的输出;
本质上可以分成 ss.fit(X_train) 和 ss.transform(X_train)两步完成
下面分开写 和 X_train = ss.fit_transform(X_train) 等价
#ss.fit(X_train)
#X_train = ss.transform(X_train)
和训练集不同,为何测试集不用fit,而直接进行transform?
X_test = ss.transform(X_test)
X_test
那么是否可以写成 ss.fit_transform(X_test)
如果加了fit,那么图纸中的[μ1~μn] 和[σ1~σn] 就会发生变化。
本来使用的是x_train的[μ1~μn] 和[σ1~σn]
现在变成了x_test的[μ1~μn] 和[σ1~σn]
这点要注意。
10、 模型训练
lr = LinearRegression()
## LinearRegression 是一个有监督的算法,所以要把特征值和目标值一起放入
lr.fit(X_train,Y_train) #训练模型
## 模型校验
y_predict = lr.predict(X_test) #预测结果
## 回归的默认评价指标为R^2
#R^2 :可解释方差的回归评分函数 (explain_varicance_score)
#R^2 = 1 - ( ∑ ( 预测值 - 真实值 )^2 / ∑ (真实值 - 平均值)^2 )
#R的取值范围是 (-∞,1),R越接近1,说明预测结果越好。
## 注意:lr.score输入了特征X_train后会计算出预测值 y_predict
## 最终用y_predict和Y_train进行比较评分
## 而不是直接拿X_train和Y_train比较
## lr.fit(X_train,Y_train) 在训练完模型后会保存
## 在lr.score中会调用模型,根据X_train计算出预测值
print('训练集的R^2:' ,lr.score(X_train,Y_train))
print('测试集的R^2:' ,lr.score(X_test,Y_test))
训练集的R^2: 0.113072216845
测试集的R^2: 0.0784240135292
可见这里训练集和测试集上的R^2都不太理想
一般R^2 在0.7~0.75以上比较理想
R^2相关的介绍,请参考《05 模型训练和测试》4、回归评估指标
MSE: Mean Squared Error
均方误差是指参数估计值与参数真值之差平方的期望值;
MSE可以评价数据的变化程度,MSE的值越小,说明预测模型描述实验数据具有更好的精确度。
RMSE
均方误差:均方根误差是均方误差的算术平方根
mse = np.average((y_predict-Y_test)**2)
rmse = np.sqrt(mse)
print('rmse: ',rmse)
rmse: 1.09366130101
11、模型保存、持久化
from sklearn.externals import joblib
joblib.dump(ss,'data_ss.model') #保存标准化模型
joblib.dump(lr,'data_lr.model') #保存回归模型
s1 = joblib.load('data_ss.model') #加载模型
s2 = joblib.load('data_lr.model') #加载模型
12、查看预测结果和真实结果的图形
对于X的列:[年月日 时分秒]
目前没有什么技术可以将6个特征绘制到一个坐标轴上
那么如何在二维的坐标平面里反映真实值和预测值的关系?
横坐标和纵坐标分别用什么单位来表示?
横轴:观测值的序号
纵轴:每个样本对应的真实值和预测值 (功率)
预测值和实际值画图比较
## 横坐标,一共多少个测试样本
t=np.arange(len(X_test))
plt.figure(facecolor='w') #建立一个背景色是白色的画布
plt.plot(t,Y_test,'r-',linewidth=2,label='真实值')
plt.plot(t,y_predict,'g-',linewidth=2,label='预测值')
plt.legend(loc='upper right') # lower left
plt.grid(True) #网格是否显示
plt.show()
由上面的案例我们可以看到:
训练集上表现得不好,那么测试集上的效果肯定也不好,即欠拟合。
训练集上表现得好,测试集表现得不好,即过拟合。
如何解决本案例中遇到的欠拟合问题?
1、增加数据集中的观测值 (样本数量)
2、增加数据的维度 (特征数量)
仿照预测时间与功率的线性关系 (由于时间和功率之间不存在线性关系,所以最后的效果很差)
试着预测电流和功率之间的关系 (电流和功率之间的关系我们已知是线性关系,所以结果会非常好)