一、背景
看见这种以人名命名的理论我都会查一下这个人到底是谁,这是百度百科里贝叶斯的头像:
这一身神甫打扮不禁让我想起了豌豆狂魔孟德尔,于是我又在网上搜索一下“贝叶斯生平”,发现了一篇奇文《贝叶斯身世之谜》,长篇大论地研究了一下贝叶斯到底是哪一年出生的,末尾还对贝叶斯的头像真实性提出了质疑。这还是发在《统计研究》(中文核心期刊)的正经的期刊文献。
我只想问一句,读研期间发了这样的论文给毕业吗???
二、思路
贝叶斯公式
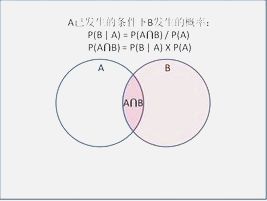
我在百度百科发现这么一张配图:
我们就按照这张图来讲吧,事件A发生的概率为P(A);事件B发生的概率为P(B);在事件A发生的条件下事件B发生的概率为P(B|A);在事件B发生的条件下事件A发生的概率为P(A|B);事件A,B同时发生的概率为P(A∩B)。
可以得到P(A∩B)=P(A)×P(B|A),同样的P(A∩B)=P(B)×P(A|B)
那么有P(A)×P(B|A)=P(B)×P(A|B)转化一下变成P(B|A)=P(A|B)×P(B)/P(A),这就是我们后面需要用到的公式。
朴素贝叶斯分类器
假设一个样本,每个个体有四个特征参数,分别为F1,F2,F3,F4,有两个类别,分别为C0,C1。
那么对于某个特定的样本,其属于C0类的概率为:P(C0|F1F2F3F4)=P(F1F2F3F4|C0)×P(C0)/P(F1F2F3F4)
属于C1的概率为:P(C1|F1F2F3F4)=P(F1F2F3F4|C1)×P(C1)/P(F1F2F3F4)
朴素贝叶斯之所以有朴素两个字,就是因为它把问题简化了,假设所有特征参数均相互独立,这样就有:
P(F1F2F3F4|C0)=P(F1|C0)×P(F2|C0)×P(F3|C0)×P(F4|C0)
我们把这个式子带回去,朴素贝叶斯分类就变成了比较P(F1|C0)×P(F2|C0)×P(F3|C0)×P(F4|C0)×P(C0)以及P(F1|C1)×P(F2|C1)×P(F3|C1)×P(F4|C1)×P(C1)两个量那个大的问题。
三、代码
这次的实例与上一篇k近邻算法相同,我们直接使用上次经过归一化处理之后的数据。
BallMillAbility OreGrade RateofMagnet TailGrade ConcentrateGrade
0 0.508755 0.526555 0.418244 0.325203 0.0
1 0.436707 0.481032 0.567986 0.443089 1.0
2 0.529417 0.412747 0.459552 0.483740 1.0
3 0.000000 0.613050 0.656627 0.609756 1.0
4 0.704730 0.464340 0.786575 0.723577 1.0
5 0.569675 0.429439 0.464716 0.686992 0.0
6 0.545946 0.347496 0.431153 0.752033 1.0
7 0.305294 0.391502 0.555077 0.609756 0.0
8 0.594509 0.335357 0.444062 0.776423 1.0
9 0.506505 0.074355 0.302926 0.691057 1.0
.. ... ... ... ... ...
处理数据
由于我们的数据是连续性数据,所以要先对数据进行区间分级:
for i in range(149):
df['BallMillAbility'][i] = int(df['BallMillAbility'][i]/0.1)
df['OreGrade'][i] = int(df['OreGrade'][i]/0.1)
df['RateofMagnet'][i] = int(df['RateofMagnet'][i]/0.1)
df['TailGrade'][i] = int(df['TailGrade'][i]/0.1)
得到:
BallMillAbility OreGrade RateofMagnet TailGrade ConcentrateGrade
0 5.0 5.0 4.0 3.0 0.0
1 4.0 4.0 5.0 4.0 1.0
2 5.0 4.0 4.0 4.0 1.0
3 0.0 6.0 6.0 6.0 1.0
4 7.0 4.0 7.0 7.0 1.0
5 5.0 4.0 4.0 6.0 0.0
6 5.0 3.0 4.0 7.0 1.0
7 3.0 3.0 5.0 6.0 0.0
8 5.0 3.0 4.0 7.0 1.0
9 5.0 0.0 3.0 6.0 1.0
.. ... ... ... ... ...
我们假设一个样本归一化处理之后是这样的:
(这里之所以不使用上一篇文章中的那个样本是因为,那个样本最后预测出来的结果合格概率为0,太过绝对,所以我换了一个测试样本,应该是因为样本数量不够大才出现这种情况)
BallMillAbility OreGrade RateofMagnet TailGrade ConcentrateGrade
6.0 2.0 1.0 7.0 --
两个变量的比较
指标合格的可能性:
P(F1|C=1)×P(F2|C=1)×P(F3|C=1)×P(F4|C=1)×P(C=1)
不合格的可能性:
P(F1|C=0)×P(F2|C=0)×P(F3|C=0)×P(F4|C=0)×P(C=0)
统计方法很简单:
m = 0
for i in range(149):
if df['BallMillAbility'][i] == 6 and df['ConcentrateGrade'][i] == 1:
m+=1
print(m/149)
合格:0.0738×0.0469×0.0067×0.0402×0.3356=0.0000003128
不合格:0.1812×0.0604×0.0201×0.0738×0.6644=0.00001078
不合格的概率是合格的概率的34.46倍,基本可以确定这个样本为不合格样本。
四、总结
- 这次讲的跟上次一样,是一个没有不包含模型训练这一环节的简单预测模型,可以看到我们预测的结果比k近邻算法得到的结果倾向性更强一些。
- 使用这个方法最好数据量大一些,否则会出现某一项概率为零的情况,这样就不好估计了。