有个段子。在太平洋某小岛上发现了几个原始部落,老大们聚会,互相比拼谁识的数大,一个首领先说了一个“3”,第二个首领想了半天,说:“你赢了。”
在人类漫长的演化过程中,生活环境相对简单,没什么特别大的数字需要考虑,其实是不需要概率思维的。恰恰相反,为了更好的生存,人们甚至需要夸大或者歪曲某些危险的概率,快速的做决定等,这也就是思维偏差的由来。事实也是如此,概率这个概念基本是到了十七世纪才提出来。
《随机漫步的傻瓜》这本书是塔勒布的成名作,核心思想是讲金融行业里充斥着大量的连续数年业绩很好却是因为运气的宠儿,其实他们都是随机性的产物,并非真正有本事,随着时间的推移,他们早晚会被淘汰。这本书虽然有些青涩,但是也已经具备了塔勒布关于不确定性、黑天鹅等概念的主要思想。而从写作的文学性上来说,我反而觉得是三本里最佳。
这里,主要谈谈里面关于概率的一些看法。
概率和期望值
春节度假,你有两个选择,一个是去泰国,一个是去长白山,但是你去泰国的概率是80%。你的脑海里既可以想象在泰国的沙滩上沐浴阳光的慵懒惬意,又可以想像在长白山滑雪的英姿飒爽。但是你能想象头顶是泰国的阳光脚下是长白山的雪吗?或者换句话说,你能想象80%去泰国是什么意思吗?
罗胖在跨年演讲里举的那个例子,一个按钮肯定可以得到100万,另外一个有50%的概率得到1个亿。为什么很多人选前者,就是他们无法想象,在这里“5000万(1亿x50%)”是个什么概念。
我们天生就是概率盲。
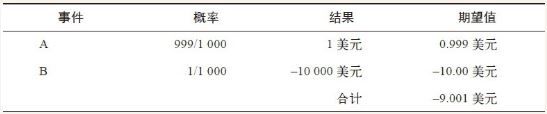
一个游戏如果有1000次里有999次获胜,每次可以赚1美金,但是有一次会赔10,000美金,这其实就不值得参与。
很多人看到上述图表都会头脑清晰,但是开车看手机时有没有想过这个问题呢?
同样的道理,在股市里,你看准涨跌不重要,关键是涨跌的幅度,以及你的仓位。你不会因为预测的频率而致富。
我们需要什么样的历史观
我们经历的现实只是所有可能出现的随机历史中的一个,我们却因为它出现了而误将它当作最可能出现的那个,忘了还有其它可能性,甚至是更大的可能性。
我们非常不善于考虑“另类历史”,而更习惯于以成败论英雄。亚历山大帝和凯撒的确是战功卓著,他们聪明、勇敢、高尚,但是同期也有其他很多同样聪明、勇敢、高尚的人,但是战败了。我们不否认他们打了胜仗,但是我们对胜利和他们的品质之间的因果关系表示怀疑。
值得欣慰的是,作者在《伊利亚特》中发现,诗人并没有以成败论英雄,英雄之所以是英雄,是因为他们的行为十分英勇,而不是因为战场上的成败。这里让人想到日本人的英雄观,他们最敬仰的是历史上那些历尽艰苦卓绝却失败的人,这样的人被他们奉为英雄。而我们,貌似从项羽以后,就是成王败寇了。
样本,一切都有关于样本
一半以上的概率错误,都和样本有关,要么样本不够全,要么样本不够多。
某人过去的表现优于他人,的确我们可以推测他未来的表现也会更好,但是这种推测其实非常弱,完全取决于:他从事工作的随机成分多少,以及有多少样本数。
一个基金经理过去几年的业绩好,这个信息如果不考虑样本的大小,就是一个无效信息。如果样本总共只有10个人,那你可以放心的把一半的钱交给他,如果样本是1万个人,你则可以完全视而不见。
5只猴子打出一首莎士比亚的十四行诗,那肯定是稀奇的,如果有1亿只猴子,就不是了,或者,打不出来那才稀奇呢。
有人采用一种“罗宾汉”策略选择基金经理,他们不相信过去几年表现好的,认为有均值回归效应,应该选表现差的,这样在未来获利的概率更大。这个选择同样是危险的,因为表现不好的基金经理,接下来有两种情况,有的的确会表现变好,而有的则会退出市场,后者不会出现在统计样本中。要真做这个决定,那你得必须找到有过少人退出了。
沉默的证据,死者不说话,这些思维偏差,或者谬误,说到底,都是样本数不够全,或者不够多。
很多巧合,其实没那么巧
随便找一个人,你和他碰巧生日是同一天的概率是1/365,因此在班级里,公司里,聚会中,你碰到一个生日和你同一天的人,总感到是意外的缘分,值得大谈特谈。其实一个房间里如果有23个人,那么任意两人生日同一天的概率高达50%,如果是70人,则高达99%。具体计算就是1减去任意两人都不可能是同一天的概率。
你和任何你以前认识的人,在任何地点偶遇的概率并不低,比你想象中的高很多。
如果有人找到了股市波动和政府宣布的某件事情相关时,你最好也不要相信,你如果交给计算机处理,肯定能找到很多虚假相关性,比如股市的涨跌竟然和姑娘的裙子高度有关。所谓的《圣经密码》可以做出预测,也是同样的道理。
独立事件和赌徒谬误
赌徒谬误的根源就在于无法理解什么是独立事件。独立事件说的是,以前发生的任何结果都不影响该事件未来发生的概率。
一件事情发生的概率是1%,不意味必须得尝试100次才发生,有可能第一次就发生了,也有可能第10次就发生了,它只意味着发生之后未来可能是100次才发生一次。
赌大小的游戏,下面哪一个出现的概率更高?
大大大大大
大大大大小
大小大小大
正确的答案是一样高,都是50%x50%x50%x50%x50%=3.13%。而且,下一把大和小的概率也是一样的,都是50%。
联合概率低于任一事件的独立概率
倍受塔勒布推崇的丹尼尔.卡尼曼 (《思考,快与慢》的作者)有个案例,琳达,31岁,单身,一位直率又聪明的女士,主修哲学。在学生时代,她就对歧视问题和社会公正问题较为关心,还参加了反核示威游行。那么下面两个选项,哪一个可能性更大?
琳达是银行出纳。
琳达是银行出纳,同时她还积极参与女权运动。
令人惊讶的是,在几次调查中,85-90%的大学生选择了第二个。这再一次说明了,我们的大脑先天不适合处理概率问题。
你对概率的直觉有时错的离谱
书中还引用了本内特《你赌对了吗?》(Deborah Bennett, Randomness)书中的一个例子:
检验某种疾病时有5%的概率产生误诊(false positives),全部人口有1‰的概率患这种疾病。如果你被检查出来呈现阳性,那么你真正患上这种疾病的概率有多少?
相信你肯定吓坏了,因为实测下来,大部分医生都回答95%。而正确的答案是接近2%,只有不到1/5的专业人士答对。
可以这么考虑:假设没有误诊存在,那么1000个受检的病患中,预料将有一位患这种疾病。剩下的999位健康的病患中,检测的结果将有约50位染病,因为误报率是5%。所以真正患病的概率是1/51。
显著性
任何统计都有误差,当两个结果差距过小时,去探寻因果关系毫无意义。
有的新闻是这样写的,但其实这样的波动不值得任何解释。
↓ 道琼斯指数因为利率下跌而上扬1.03点
↓ 美元因为日本贸易顺差扩大而下挫0.12美元
一个人考了两次四级,一次58,一次62,你能说他第二次进步了吗?很可能这就是随机的结果。
A摩托车选手在3000公里越野赛中以几秒钟的优势赢了B选手,丝毫不能证明A更优秀,但现实中人们有时会因此去研究A是不是因为多吃了菠菜而获胜。
你已经死了 -- 条件概率
一位著名的电视金融大师发表过这样的谬论:“美国人平均可望活到73岁。因此如果你是68岁,还可以活5年,应该为此好好规划未来5年的投资。”她接着开出明确的清单,说这种人应该如何为未来5年做投资。但如果你是80岁呢?你的预期寿命是–7岁吗?
显然她把无条件预期寿命和条件预期寿命混为一谈了。你刚出生,那么你的平均预期寿命的确是73岁,但是当你活到68、80,甚至100岁时,你的预期寿命就是条件预期寿命了。否则,这就等于说,一个手术死亡率是1%。到目前为止,我们为99位病人动过手术,都很成功;你是第100位,所以你死在手术台上的概率是100%。
遍历性(Ergodicity)
金融市场上经常有人说,坏操作迟早让你吃到苦头。那个中彩票的门卫,即使活上1000年,我们也不会预期他再次获奖。但是一个拥有一身好本事却穷苦潦倒的人,最后一定会爬上来。
幸运的傻瓜可能得益于生命中的某些好运气,但是长期而言,他的处境会慢慢趋近于运气没那么好的白痴。每个人都会向长期的性质靠拢。
所谓出来混,早晚都要还的。
优雅地与概率平起平坐
既然我们知道这个世界上很多事情都是随机的,不必然是有因果关系的 ,那么我们就应该力争优雅的面对那些小概率的失败和苦难。
塔勒布写到:
行刑日那天把最好的衣服穿上(仔细刮好胡子);挺直腰杆站直,显现一股傲气,好在行刑队心里留下美好的印象。诊断出罹患癌症时,不要哭天喊地,一副无辜受害的样子。只和医生讨论病情,切莫让别人知道,如此就可避免听到老掉牙的安慰话,也没人会视你为值得同情的受害人;此外,那种有尊严的态度,可以让挫败和胜利一样,都叫人觉得具有英雄气概。赔钱的时候,务必对你的助理更为客气,不要对他发怒(许多交易员经常这个样子,令人不齿)。不要将你的命运怪罪于任何人,即使他们确实是祸首也是一样。就算你的另一半和英俊的滑雪教练或年轻但野心不小的模特儿搞上,也绝不要自怜自艾。别怨东怨西。如果你的生意变少,不要马上哈腰屈膝,可以像我儿时的好友艾波史雷曼那样,发出一封充满英雄气概的电子邮件给同行,告诉他们:“生意虽少,态度不变。”
命运女神唯一不能控制的东西,是你的行为。