Ensemble learning involves combining multiple machine learning techniques into one predictive model in order to create a stronger overall prediction, which means to decrease variance and bias.
Bias and Variance in Ensemble learning
Error due to Bias: The error due to bias is taken as the difference between the expected (or average) prediction of our model and the correct value which we are trying to predict.
Error due to Variance: The error due to variance is taken as the variability of a model prediction for a given data point.
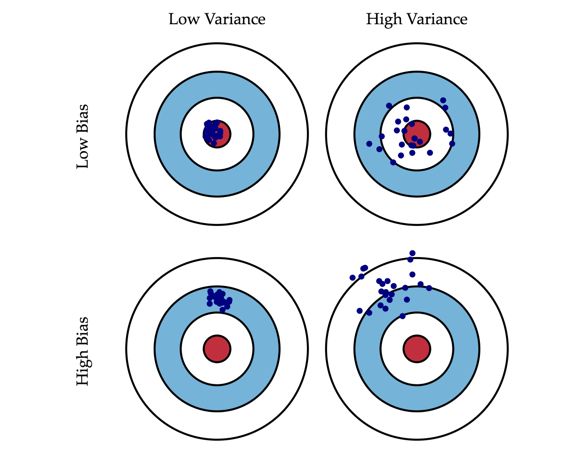
We can plot four different cases representing combinations of both high and low bias and variance (Assume that red spot is the real value and blue dots are predictions) :
Bagging
Bagging (stands for Bootstrap Aggregation) is a simple ensemble method by taking multiple random samples(with replacement) and using each of these samples to construct a separate model and separate predictions. These predictions are then averaged to create a final prediction value.
Bagging for Bias
As Bagging takes random samples from data and then build same model, so based on E[∑ Xi/n ]=E[Xi] (1) this basic statistical equation, so the bias for final prediction value is almost as same as for each model's prediction value. So bagging needs "strong learner" as base learner.
Bagging for Variance
In addition, we know that Var(∑Xi/n)=Var(Xi)/n is true if each model is independent and then the variance will be decreased a lot in this case. While Var(∑Xi/n)=Var(Xi) is true if all the models are same and then the variance stays the same. The models in Bagging are dependent but not same (as the random sample and same model), so the variance for bagging is the intermediate state of the above two extremes. To make it clearer, suppose we have n i.d. random variables with positive pairwise correlation ρ, and each has variance σ², then the variance of the average is:
Thus Bagging can decrease variance as it can decrease the second term. To decrease variance more, models in bagging should have less correlation, such as random forest.
Random Forest
As mentioned above, the base model in random forest has lower correlation by taking random samples and part of features(usually √p, denote p as number of features). In this way, random forest builds a large collection of de-correlated trees, and then averages them. Thus random forest can decrease both the first term and second term.
Boosting
Boosting for Bias
Boosting is an iterative technique which adjust the weight of an observation based on the last classification. If an observation was classified incorrectly, it tries to increase the weight of this observation and vice versa.
From the optimization point of view, Boosting is using forward-stagewise method to minimize the loss function. In this way, Boosting can be seen as a way of fitting new model to minimize the following loss function
step by step. As a result, the bias decreases sequentially.
Boosting for Variance
In Boosting, each model is based last one, so the correlation in models are high. As a result, the variance is high. Boosting can not decrease variance.
Adaboost
The first realization of boosting that saw great success in application was Adaptive Boosting or AdaBoost for short.
By changing the weights of the training samples based on the errors in each iteration, Adaboost learns a number of different classifiers by same base model, and linearly combines these classifiers to improve the classification performance.
In addition, AdaBoost is equivalent to Forward Stagewise Additive Modeling using the exponential loss function.
AdaBoost can be sensitive to outliers and noise because it is fitting to an exponential loss function, and the exponential loss function is sensitive to outliers/label noise. It is quite clear that if there exists an outlier/noise, this prediction would suffer a large loss/penalty since the penalty is exponentiated (exp(-f(x)*y)). So the classifier will be influenced when trying to minimize the loss function. There have been several papers on using various other loss functions with boosting that result in less sensitivity to outliers and noise, like SavageBoost.
Gradient Boosting
AdaBoost and related algorithms were recast in a statistical framework first by Breiman calling them ARCing algorithms.
Arcing is an acronym for Adaptive Reweighting and Combining. Each step in an arcing algorithm consists of a weighted minimization followed by a recomputation of [the classifiers] and [weighted input].
— Prediction Games and Arching Algorithms [PDF], 1997
This framework was further developed by Friedman and called Gradient Boosting Machines. --Greedy Function Approximation: A Gradient Boosting Machine [PDF], 1999.
The gradient boosting method is:
In each stage, Boosting introduce a weak learner to compensate the
shortcomings of existing weak learners. From this point of view, “shortcomings” are identified by gradients in Gradient Boosting, and are identified by high-weight data points in Adaboost.
Elements in Gradient Boosting
Gradient boosting involves three elements:
A loss function to be optimized.
The loss function must be differentiable. But it used depends on the type of problem being solved. For example, regression may use a squared error and classification may use logarithmic loss. Also you can define your own, any differentiable loss function can be used.A weak learner to make predictions.
Decision trees are widely used as the weak learner in gradient boosting.An additive model to add weak learners to minimize the loss function.
Traditionally, gradient descent is used to update a set of parameters, such as the coefficients in a linear regression or weights in a neural network, to minimize the loss function. After calculating error or loss, the weights are updated to minimize that error.
Instead of parameters, we have weak learner sub-models or more specifically decision trees. In Gradient Boosting, we modify the parameters of a new tree, then move in the right direction by reducing the residual loss.
Generally this approach is called functional gradient descent or gradient descent with functions.
One way to produce a weighted combination of classifiers which optimizes [the cost] is by gradient descent in function space
— Boosting Algorithms as Gradient Descent in Function Space [PDF], 1999
Regularization in Gradient Boosting
Gradient boosting is a greedy algorithm and can overfit a training dataset quickly. So regularization will help a lot.
- Tree Constraints
When we use tree as base learner, we can set some constraints to keep the tree as weak learner: - Depth
- Number of Trees
- Number of nodes or leaves
- Minimum improvement of loss
- Shrinkage
The simplest implementation of shrinkage in the context of boosting is to scale the contribution of each tree by a factor 0 <ν< 1 when it is added to the current approximation.
—The Elements of Statistical Learning, P383
The ν, also called learning rate, is common to set in range of 0.1 to 0.3. With smaller learning rate, the number of iteration of boosting will increase, so it takes more time to train. It is a trade-off between the number of trees and learning rate.
- Random sampling
We can learn from random forest that trees created from subsamples of the training dataset can decrease the variance. This method also can be used to decrease the correlation between the trees in the sequence in gradient boosting models.
This variation of boosting is called stochastic gradient boosting.
At each iteration a subsample of the training data is drawn at random (without replacement) from the full training dataset. The randomly selected subsample is then used, instead of the full sample, to fit the base learner.
— Stochastic Gradient Boosting [PDF], 1999
A few variants of stochastic boosting that can be used:
- Subsample rows before creating each tree.
- Subsample columns before creating each tree
- Subsample columns before considering each split.
Random forest uses the second method, subsample columns to decrease the corrleation between base learners a lot.
According to user feedback, using column sub-sampling prevents over-fitting even more so than the traditional row sub-sampling
— XGBoost: A Scalable Tree Boosting System, 2016
- Penalized Learning
Just like lasso and ridge, we can also add L1 and L2 regularization in Gradient Boosting.
Classical decision trees like CART are not used as weak learners, instead a modified form called a regression tree is used that has numeric values in the leaf nodes (also called terminal nodes). The values in the leaves of the trees can be called weights. The leaf weight values of the trees can be regularized using popular regularization functions.
Of course there is more than one way to define the complexity,The below one works well in practice.
The additional regularization term helps to smooth the final learnt weights to avoid over-fitting. Intuitively, the regularized objective will tend to select a model employing simple and predictive functions.
— XGBoost: A Scalable Tree Boosting System, 2016
Stacking
To be continued....
Reference:
- Understanding the bias and variance
- The Elements of Statistical Learning
- Gradient_boosting