排序

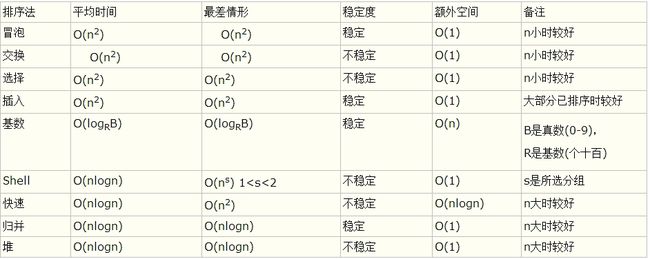
稳定性

假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，ri=rj，且ri在rj之前，而在排序后的序列中，ri仍在rj之前，则称这种排序算法是稳定的；否则称为不稳定的。

堆排序、快速排序、希尔排序、直接选择排序不是稳定的排序算法，而基数排序、冒泡排序、直接插入排序、折半插入排序、归并排序是稳定的排序算法。

复杂度

复杂度

堆排序

小顶堆过程：

1. 自下往上， 调整父节点>=子节点, root节点得到最大值， 类似于一趟冒泡过程；
   2.把root值放到最后面， 剩下的重复第一步， 得到次最大值， 放到次后面 重复这个步骤, 熟悉的两层循环， 注意了， 这里数组下标从1开始。

void HeapSort(SqList* L)
{
    for (i = L->length; i > 1; i--)
    {
        for (int j = i/2; j >= 1; j--) {  //找到前i个结点的最大值过程
            HeapAdjust(L, j, i);
        }
        
        swap(L,1,i); //把最大值放到最后
    }   
}

HeapAdjust(SqList* L, int s, int m)  //调整父节点的值大于等于子节点
{
    if (s*2 <= m && L->r[s * 2] > L->r[s] ) {    
       swap( L->r[s] , L->r[s * 2]);
    } 
  
   if (s *2 + 1 <= m && L->r[s *2 + 1] > L->r[s]) {
         swap(L->r[s], L->r[s *2+ 1]);
} 

下面是一个优化版的, 优化版优化在于
1. 调整父节点比子节点要大时采用递归操作；
2.第二趟冒泡的时候， 不再是从下往上调整， 而是从上往下调整;
void HeapSort(SqList* L)
{
    int i;
    for (i = L->length/2; i >=1 ;i--)  //找到最大值；
    {
        HeapAdjust(L, i, L->length);
    }
    for (i = L->length;i >1; i--)
    {
        swap(L,1,i); 
        HeapAdjust(L, 1, i-1); //优化了 
    }   
}

HeapAdjust(SqList* L, int s, int m)  //调整父节点的值大于等于子节点以及子节点
//大于等于子子节点
{
    int temp, j;
    temp = L->r[s];
    for(j = s*2; j<=m;  j = j*2)
    {
        if (j + 1<= m && L->r[j] < L->r[j+1])  子节点最大值, 如果没有右节点，
//则左节点最大
            j++;
        if (temp >= L->r[j])
            break;

        swap(L->r[j/2] , L->r[j]);   //父节点小于子节点
    } 
}

快速排序

1.i =L; j = R; 将基准数挖出形成第一个坑a[i]。
2.j--由后向前找比它小的数，找到后挖出此数填前一个坑a[i]中。
3.i++由前向后找比它大的数，找到后也挖出此数填到前一个坑a[j]中。

int AdjustArray(int s[], int l, int r) {  //返回调整后基准数的位置 
    int i = l, j = r; 
    int x = s[l]; //s[l]即s[i]就是第一个坑 
    while (i < j) { 
        // 从右向左找小于x的数来填s[i] 
        while(i < j && s[j] >= x) j--;   
        if(i < j) { 
            s[i] = s[j]; //将s[j]填到s[i]中，s[j]就形成了一个新的坑 
            i++; 
        } 

        // 从左向右找大于或等于x的数来填s[j] 
        while(i < j && s[i] <= x) i++;   
        if(i < j) { 
            s[j] = s[i]; //将s[i]填到s[j]中，s[i]就形成了一个新的坑 
            j--; 
        } 
    } 
    //退出时，i等于j。将x填到这个坑中。 
    s[i] = x;   //补坑千万不要忘记了

    return i; 
} 

void quick_sort1(int s[], int l, int r) 
{ 
    if (l < r) { 
        int i = AdjustArray(s, l, r);//先成挖坑填数法调整s[] 
        quick_sort1(s, l, i - 1); // 递归调用   
        quick_sort1(s, i + 1, r); 
    } 
}

归并排序

1.先对半分， 兵分两路
2.使用辅助数组把两路合并起来

void mergearray(int a[], int first, int mid, int last, int temp[]) 
{ 
    int i = first, j = mid + 1; 
    int m = mid,   n = last; 
    int k = 0; 

    while (i <= m && j <= n) 
    { 
        if (a[i] <= a[j]) 
            temp[k++] = a[i++]; 
        else 
            temp[k++] = a[j++]; 
    } 

    while (i <= m) 
        temp[k++] = a[i++]; 

    while (j <= n) 
        temp[k++] = a[j++]; 

    for (i = 0; i < k; i++) 
        a[first + i] = temp[i]; 
} 
void mergesort(int a[], int first, int last, int temp[])  { 
    if (first < last)  { 
        int mid = (first + last) / 2; 
        mergesort(a, first, mid, temp);    //左边有序 
        mergesort(a, mid + 1, last, temp); //右边有序 
        mergearray(a, first, mid, last, temp); //再将二个有序数列合并 
    } 
}