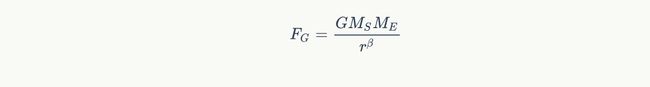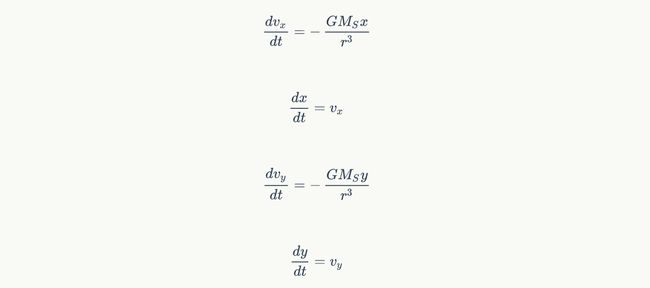1.摘要

本次作业模拟了天体的运行轨迹，探究了问题4.8、4.9

比较了如果不是平方反比定律，即β不等于2，等于其他值的时候，模拟的椭圆轨道变化

2.背景介绍

天体运行遵循平方反比的万有引力定律（公式中的β=2）

讲围绕太阳运动天体受力分解成x,y轴方向得到

我们可以运用以前用过的Euler-Cromer方法用程序计算上面四个式子

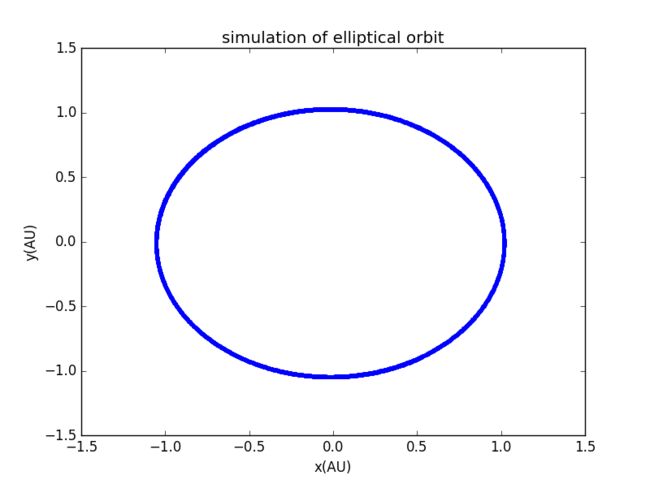
按行星椭圆运动，我取初始条件为x=a(1+e),y=0,Vx=0,Vy=Vmin

初始条件是

但显然这只是天体运动的简单模型，没有考虑相对论等其他效应，且目标物体较少，

运用这个简单的模型，可以验证开普勒第三定律的正确性，并将计算出来的T^2/a^3与书上的理想值进行比较

行星运动是美丽的

1、八大行星加上冥王星的模拟运行轨迹图

代码：九个星球运行轨迹

用VPython模拟的运行图为

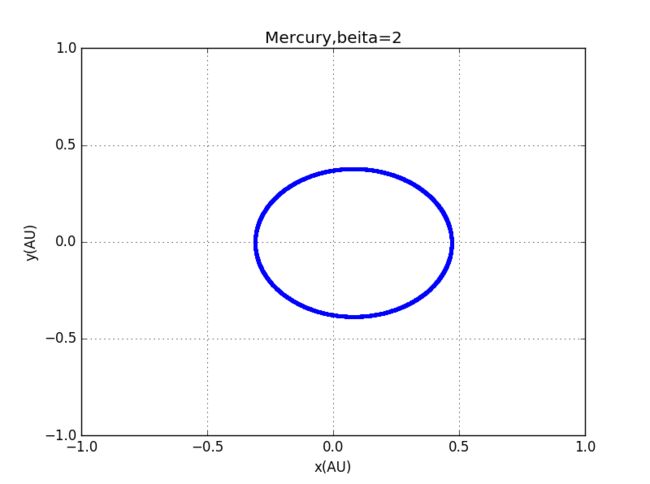
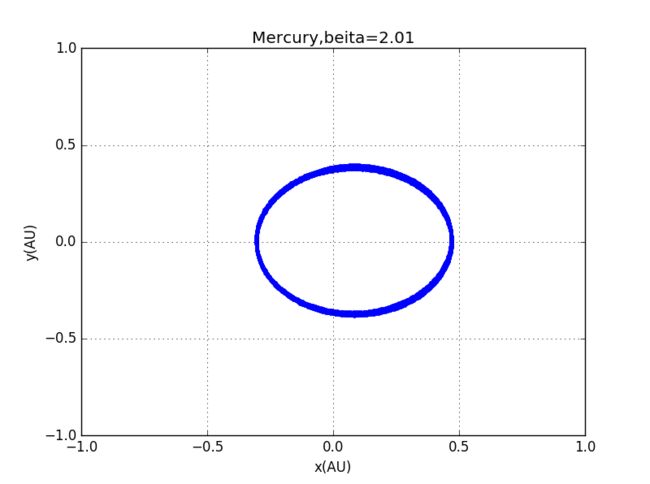
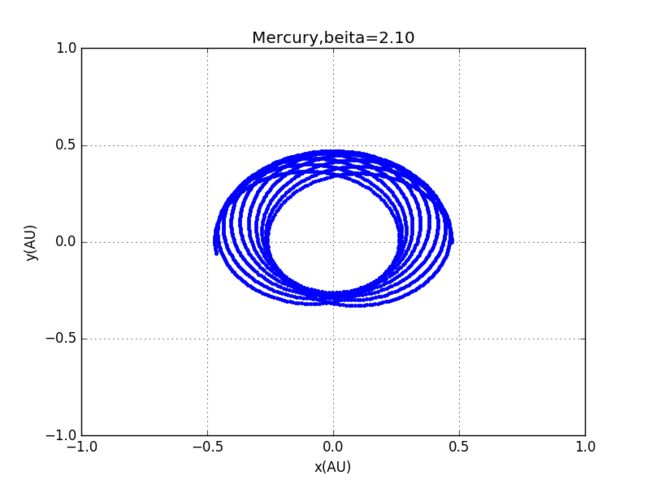
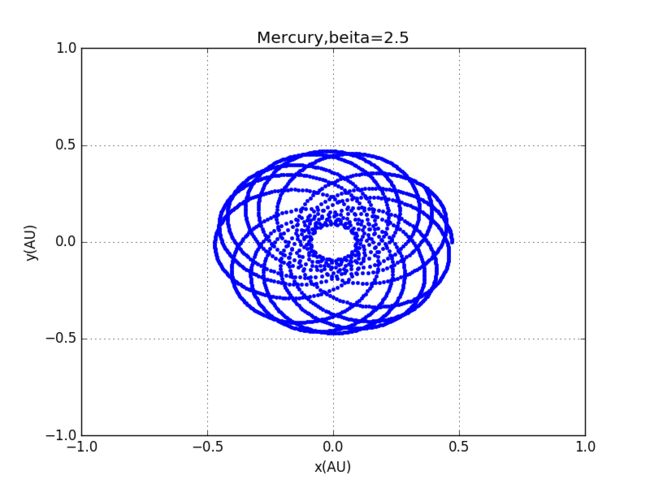
2、初始条件相同的行星运动椭圆轨道，β=2, β=2.01, β=2.1，β=2.5, β=3时的轨道模拟如下：

代码：水星的不同β值轨迹图

以上用的是水星的参数

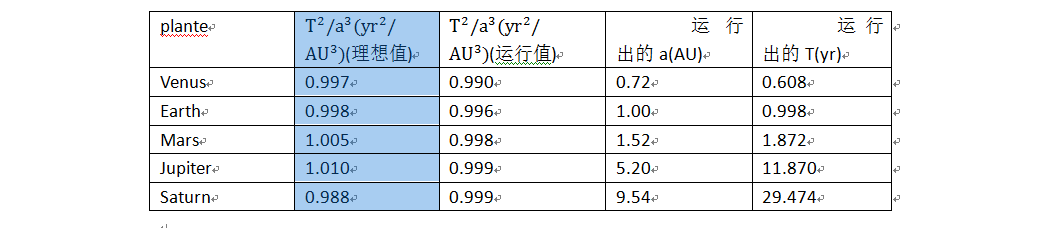
3、验证开普勒第三定律并且与理想值比较

代码：开普勒第三定律

运行上述程序过程中，可以取其中一些点，计算可知道开普勒第三定律成立的

计算出来的五个行星的T^2/a^3值

与理想值相比运行得出的值还是有一定差距的，考虑到我只取了一组点计算T^2/a^3,并且每一步的时间距离为0.001年，还是比较大的，所以误差也在一定情理之中。

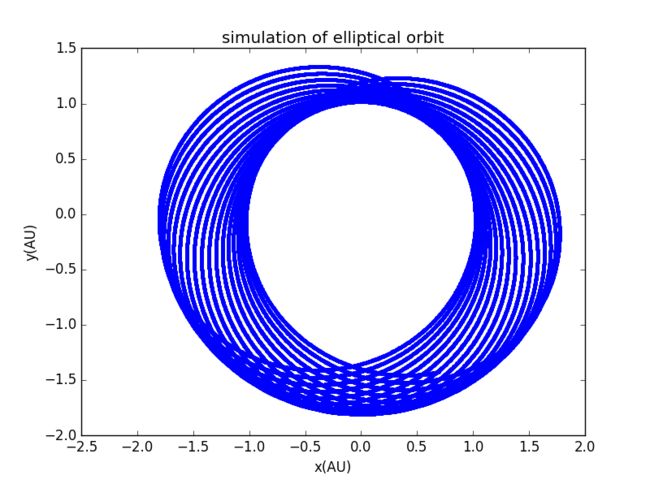
4、如问题4.9所述，我取β=2.05，比较不同初始轨道的形状与轨道旋转的快慢关系

代码：problem4.9

取不同的初始值，使轨迹呈现不同的形状（很圆——很椭圆）

取地球的参数

初始x=a(1+e),y=0,vx=0,当vy差不多等于2π时，轨迹是比较圆的，并且轨迹近似没有旋转

但是当vy偏离2π，如vy=6.5时，轨迹向椭圆变化，轨迹旋转（图上点比较密集）

vy=7和vy=8如下

vy=7

vy=8

可以看出轨迹加速旋转

1、验证了开普勒第三定律的正确性

2、计算了五颗行星的T^/a^3

3、当平方反比定律不再适用，行星轨道将不再固定，β=2.01时，轨道开始轻微旋转，，β=2.1时，轨道显著旋转，β=2.5时，单个轨道都是椭圆，但轨道整体大约是绕着一点旋转，β=3时，运行轨迹将不再闭合。这暗示我们可以通过观察不同行星运行轨迹变化，看它脱离平方反比的程度有多大

4、行星运动轨迹偏向于圆时，轨迹整体旋转将不如偏向于椭圆时旋转的快

计算物理课本