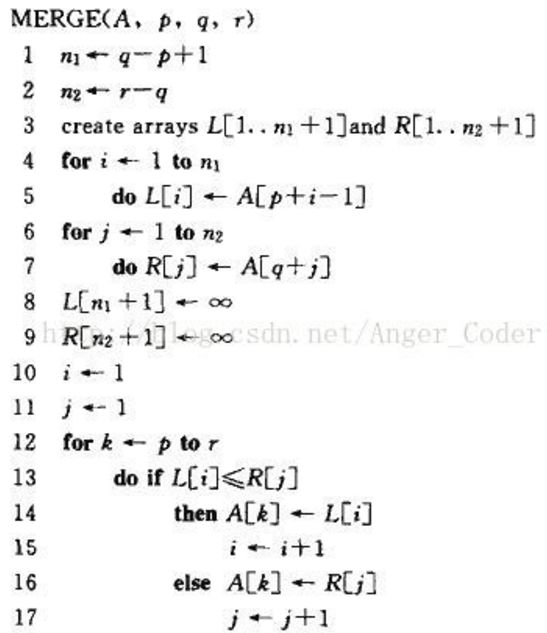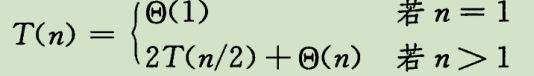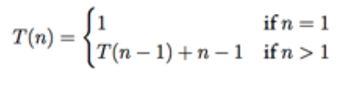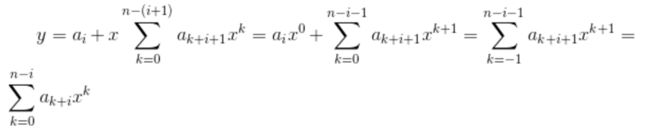这一章介绍贯穿全书的框架,即设计算法的大致方法过程。以插入排序和归并排序为例,介绍描述算法的方法——伪代码,证明正确性并分析运行时间——循环不变量和效率分析,最后引入分治法。
2.1 插入排序
伪代码:用最清晰、最简洁的表示方法说明算法,主要是理顺思路。
插入排序:在一个有序数据序列中插入新的数。思路是从前到后比较查找新数的正确位置,将此位置以后的数整体后移一位,插入此数。
插入排序伪代码:
C++实现:第一个参数为待排序数组,第二个为该数组长度,下标1~ n存数共n个 。
void InsertSort(int *a, int n)
{
int i, j, t;
for (j = 2; j < 10; j++ )
{
t = a[j];
i = j - 1;
while(i > 0 && a[i] > t)
{
a[i + 1] = a[i];
i --;
}
a[i + 1] = t;
}
}
循环不变式证明正确性
对于循环不变式必须证明三条性质:
前两步类似于 数学归纳法的基本情况和归纳步,像多米诺骨牌一样。第三条通常是和导致循环条件终止的条件一起使用循环不变式。与数学归纳法不同,循环终止时停止归纳。
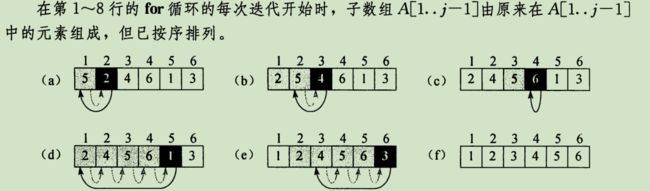
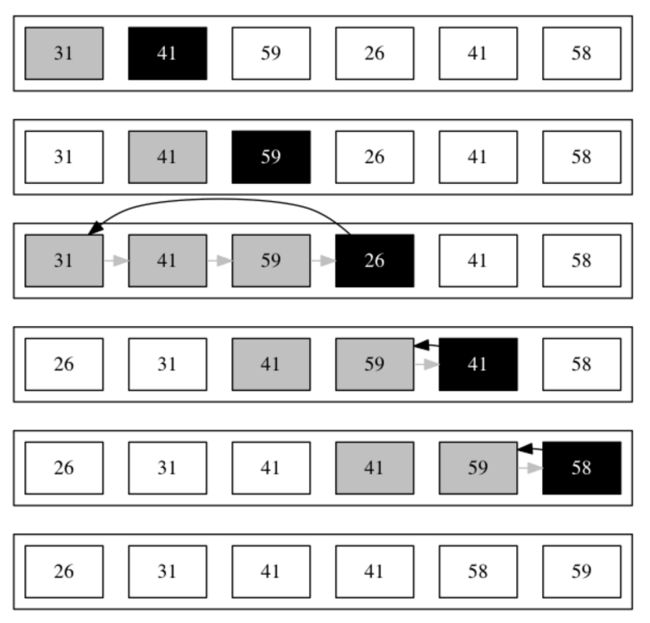
举例说明:黑色框代表当前插入数字,即下标 j 所指。A[1···j - 1]为已排好序,A[j + 1···n]为待插入数,即桌上牌堆。下图显示排序过程
此时 循环不变式就是A[1···j - 1]子数组有序
初始化:第一次循环迭代之前(j = 2),此时A[1···j - 1]子数组为A [1],循环不变式成立。
保持:伪代码4~7行将A[j - 1]、A[j - 2]等向右移动一个位置直到A[j] 的适当位置。此时子数组A[1··j]元素只是插入一个数,相对位置不变,下一次迭代保持循环不变式。
终止:终止时j = n + 1,将循环不变式中j 用n + 1带入有A[1···n]有序。
练习
2.1-1
2.1-2
INSERTION-SORT(A)
for j = 2 to A.length
key = A[j]
//Insert A[j] into the sorted sequence A[1..j-1].
i = j - 1
while i > 0 and A[i] < key // > 改 <
A[i+1] = A[i]
i = i - 1
A[i+1] = key
2.1-3
伪代码:
SEARCH(A, v):
for i = 1 to A.length
if A[i] == v
return i
return NIL
循环不变式为找过的子数组无v。
2.1-4
伪代码:
ADD-BINARY(A, B):
C = new integer[A.length + 1]
carry = 0
for i = 1 to A.length
C[i] = (A[i] + B[i] + carry) % 2 // remainder
carry = (A[i] + B[i] + carry) / 2 // quotient
C[i] = carry
return C
2.2 分析算法
插入排序算法的分析
一般来说算法需要的时间与输入的规模同步增长。输入规模根据不同问题,有时指输入中的项数,有时是用二进制表示输入时用的总位数,有时是图的边和点数。算法在特定输入上的运行时间指执行的基本操作数或步数。插入排序每步执行次数为:
所有项加起来得到总时间。但是真正关注的是 运行时间关于输入的增长量级,所以只考虑公式中最重要的项,增长量级低的算法更好。
练习
2.2-1
2.2-2
伪代码:
SELECTION-SORT(A):
for i = 1 to A.length - 1
min = i
for j = i + 1 to A.length
if A[j] < A[min]
min = j
temp = A[i]
A[i] = A[min]
A[min] = temp
C++实现:
void SelectSort(int *a, int n)
{
int i, j, min, t;
for ( i = 1;i < n; i ++)
{
min = i;
for (j = i + 1; j<= n; j ++)
{
if (a[j] < a[min])
k = j;
}
if (min != i)
{
t = a[min];
a[min] = a[i];
a[i] = t;
}
}
}
循环不变量是子数组A[1..i - 1]是原数组前i-1个最小数的有序排列。或者当前位置 i 是子数组A[i..n]的最小数的最终位置。分析初始化、保持、终止可知正确。因为n - 1个最小数排到正确位置后第 n 个自然是最大数,排最后一个。最好最坏都是Θ(n^2)
2.2-3
答:平均n/2,最坏n。运行时间都是Θ(n)。因为等可能,每个数的概率为1/n,平均查找个数为 1/n * (1 + 2 + ... +n) = (n+1)/2,Θ(n)。最坏找到最后一个或者没找到,比较 n 个,Θ(n)。
2.2-4
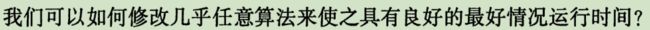
答:首先检查输入数据看是否满足某些可以直接输出的特定条件,可以输出事先计算好的结果。如:排序数组本来有序则直接输出。
2.3 设计算法
算法设计技术有很多,插入排序使用了增量法,还有很多结构递归:算法一次或多次递归地调用其自身以解决紧密相关的若干子问题。
分治法
思想:将原问题分解为几个规模较小但类似于原问题的子问题,递归地求解这些子问题,然后在合并这些子问题的解来建立原问题的解。分治模式在递归时有三个步骤:
- 分解原问题为若干子问题,这些子问题是原问题的规模较小的实例。
- 解决这些子问题,递归地求解各子问题。若子问题规模足够小则直接求解。
- 合并这些子问题的解成原问题的解。
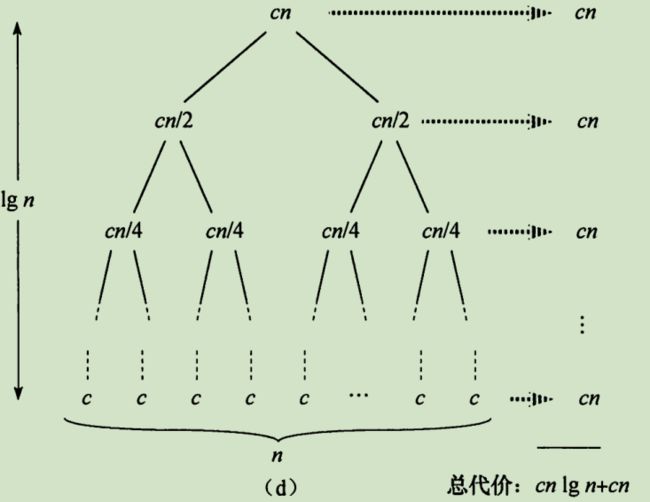
以归并排序为例:
关键是合并操作,调用MERGE(A, p, q, r),假设A[p···q]与A[q + 1 ···r]都已有序,合并成一个有序数组A[p···r]。 思路是:每次将两子数组当前元素比较,较小的加入总数组并后移该子数组指针一位。复杂度Θ(n)。伪代码:
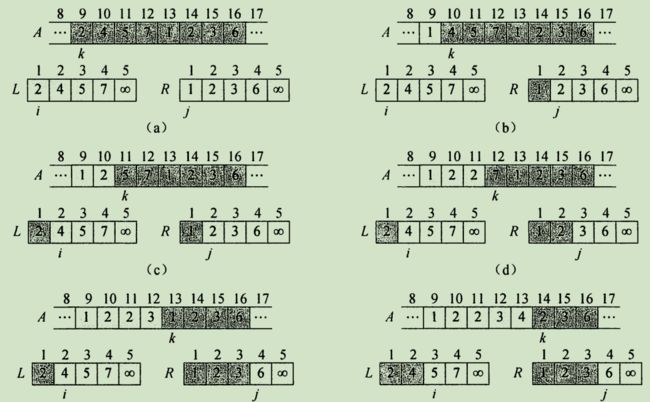
n = r - p + 1为待合并元素个数,为避免检查堆是否为空加哨兵牌无穷大。排序过程: 循环不变式: 按初始化、保持、终止的步骤分析算法正确性。归并排序伪代码:
若p>=r则子数组最多一个元素已排好,作基底情况返回。否则分两半递归排序最后合并。合并过程:
C++实现:
void Merge(int *a ,int p, int q, int r)
{
int i, j, k;
int n1 = q - p + 1;
int n2 = r - q;
int L[n1];
int R[n2];
for (i = 0; i < n1; i++)
L[i] = a[p + i];
for (j = 0; j < n2; j++)
R[j] = a[q + j + 1];
for(i = 0, j = 0, k = p; k <= r; k++)
{
if (i == n1)
a[k] = R[j++];
else if (j == n2)
a[k] = L[i++];
else if (L[i] <= R[j])
a[k] = L[i++];
else
a[k] = R[j++];
}
}
void MergeSort(int *a, int p, int r)
{
if (p < r)
{
int q = (p + r) / 2;
MergeSort(a, p, q);
MergeSort(a, q + 1, r);
Merge(a, p, q, r);
}
}
分析分治算法
算法包含递归调用时可用递归式描述运行时间。设T(n)为一个规模为n的问题的运行时间。如果问题的规模足够小,如n≤c(c为常量),则得到它的直接解的时间为常量,写作Ɵ(1)。假设我们把原问题分解成a个子问题,每一个的大小是原问题的1/b。如果分解该问题和合并解的时间各为D(n)和C(n),则得到递归式:归并排序算法的分析
- 分解:这一步仅仅是计算出子数组的中间位置,需要常量时间,因而D(n)= Ɵ(1)
- 解决:递归地解两个规模为n/2的子问题,时间为2T(n/2)
-
合并:在一个含有n个元素的子数组上,MERGE过程的运行时间为Ɵ(n),则C(n) = Ɵ (n)
递归式为: 构建递归树:
n为叶子数,把各层加起来得到Ɵ(nlgn)。
练习
2.3-1
2.3-2
MERGE(A, p, q, r)
n1 = q - p + 1
n2 = r - q
let L[1..n₁] and R[1..n₂] be new arrays
for i = 1 to n₁
L[i] = A[p + i - 1]
for j = 1 to n₂
R[j] = A[q + j]
i = 1
j = 1
for k = p to r
if i > n₁
A[k] = R[j]
j = j + 1
else if j > n₂
A[k] = L[i]
i = i + 1
else if L[i] ≤ R[j]
A[k] = L[i]
i = i + 1
else
A[k] = R[j]
j = j + 1
区别主要在for循环中加了if判断,如果其中一个子数组已经遍历完则加入另一数组元素。
2.3-3
- k = 1即n = 2时 T(2) = 2成立
- 假设n = 2^k时成立,n = 2^(k+1)时:
T(2^ (k + 1))= 2 * T(2^k) + 2^ (k + 1) = 2 * k * 2^k + 2^ (k + 1) = (k + 1)*2^ (k + 1) = nlgn
2.3-4
2.3-5
伪代码:
BINARY-SEARCH(A, v):
low = 1
high = A.length
while low <= high
mid = (low + high) / 2
if A[mid] == v
return mid
if A[mid] < v
low = mid + 1
else
high = mid - 1
return NIL
C++实现:
int BinarySearch(int *a, int length, int v)
{
int low = 0;
int high = length;
int mid;
while (low < high)
{
mid = (low + high) / 2;
if (a[mid] == v)
return mid;
if (a[mid] < v)
low = mid + 1;
else
high = mid;
}
return -1;
}
T(n) = T(n/2) + c, 故为Θ(lg n)。
2.3-6
答:不行,因为不但要查找还要移动元素。伪代码:
INSERTION-SORT(A)
for j = 2 to A.length
key = A[j]
i = BinarySearch(A[1..j-1], key) // C1 = ∑lgj {j=2 to n}
for k = j to i+1 //C2 = ∑(j/2) {j=2 to n}
A[k] = A[k-1]
A[i] = k
2.3-7
答:
- 将S排序,遍历元素 i (< x),二分查找(x - i)。运行时间 = 排序Θ(nlgn) + 遍历Θ(n)*二分查找(lgn) = Θ(nlgn)。伪代码:
PAIR-EXISTS(S, x):
A = MERGE-SORT(S)
for i = 1 to S.length
if BINARY-SEARCH(A, x - S[i]) != NIL
return true
return false
- 将S排序,设两指针指向头尾向中间扫描。
- 哈希达到Θ(n)。同LeetCode Two Sum,Python代码:
def twoSum(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[int]
"""
buff_dict = {}
for i in range(len(nums)):
if nums[i] in buff_dict:
return [buff_dict[nums[i]], i]
else:
buff_dict[target - nums[i]] = i
思考题
2-1
答:
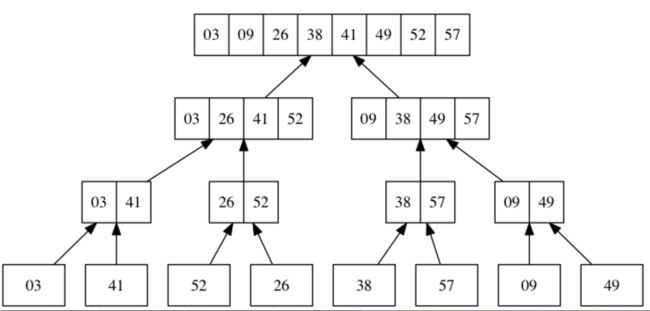
a. 长度为k的子表插入排序最坏为Θ(k^2),一共n/k个,所以总运行时间 = n/k * Θ(k^2) = Θ(nk)。
b. 根据归并排序的第归属分析可知:总代价 = 树高 * 每层代价,而每层代价常数倍的结点数。题干中 n/k 为最底层即叶子个数,每次合并减少一半,故树高为 lg(n/k) ,每层 n 个元素,所以复杂度为 n * lg(n/k) = Θ(nlg(n/k))。
c. k = Θ(lgn)。此时 Θ(nk + nlg(n/k)) = Θ(nlgn + nlg(n/lgn)) = Θ(nlgn)。
d. 根据练习1.2-2可知 n>43 mergesort 好于 insertion sort,故取 k>43 且 k + lg(n/k) < lgn的值,因为分得太细增加树高。
2-2
答:
a. 还要证明数组A中的元素还是原来的那些。
b. 循环不变式为A[j]为A[j...n]中最小的
- 初始化:刚开始只有A[n]故满足最小。
- 保持:每次循环若A[j] < A[j-1]则交换,故成立。
- 终止:j = i 时迭代结束,此时A[i]是子数组A[i..n]的最小元素。
c. 位置 i 为原数组第 i 小的数。
- 初始化:数组为空,满足。
- 保持:每次一轮内循环都满足 b 中的终止条件,即A[i]是子数组A[i..n]的最小元素。
- 终止:i = n 时迭代结束,此时A[n]是最后一个最小数。
d. Θ(n^2),同一个数量级但由于有交换操作,通常冒泡更慢。
2-3
答:
a. Θ(n)
b. 伪代码:
y = 0
for i = 0 to n
m = 1
for k = 1 to i
m = m·x
y = y + aᵢ·m
复杂度Θ(n^2),更慢。
c.
初始时: 没有项,y = 0。
- 保持:第 i 次迭代结束时:
终止:此时 i = -1,带入则为该和式。
d. 根据前三小问得出答案。
2-4
答:
a. ⟨2,1⟩, ⟨3,1⟩, ⟨8,6⟩, ⟨8,1⟩,⟨6,1⟩.
b. ⟨n,n-1,n-2,...,3,2,1⟩最多,共(n-1) + (n-2) + …… + 3 + 2 + 1 = n(n-1)/2。
c. 插入排序中移动元素的次数就是逆序数的对数。分析例子可知每次对一个小数插入时,前面每个比它大的数都要后移,个数恰好是该元素的逆序对数。
d. 归并排序merge操作时每次插入后半边子数组时,前半边还未插入的元素个数,就是逆序对数。
伪代码:
MERGE-SORT(A, p, r):
if p < r
inversions = 0
q = (p + r) / 2
// 逆序对数量 = 左分支产生的数量 + 右分支产生的数量 + 归并中产生的数量
inversions += merge_sort(A, p, q)
inversions += merge_sort(A, q + 1, r)
inversions += merge(A, p, q, r)
return inversions
else
return 0
MERGE(A, p, q, r)
n1 = q - p + 1 //前半部元素个数
n2 = r - q //后半部元素个数
let L[1..n₁] and R[1..n₂] be new arrays
for i = 1 to n₁
L[i] = A[p + i - 1]
for j = 1 to n₂
R[j] = A[q + j]
i = 1
j = 1
for k = p to r
if i > n₁ //前半部完成
A[k] = R[j]
j = j + 1
else if j > n₂
A[k] = L[i]
i = i + 1
else if L[i] ≤ R[j]
A[k] = L[i]
i = i + 1
else //后半部有更小元素
A[k] = R[j]
j = j + 1
inversions += n₁ - i
return inversions
C++实现:
void Merge(int *a ,int p, int q, int r)
{
int i, j, k, inversions = 0;
int n1 = q - p + 1;
int n2 = r - q;
int L[n1];
int R[n2];
for (i = 0; i < n1; i++)
L[i] = a[p + i];
for (j = 0; j < n2; j++)
R[j] = a[q + j + 1];
for(i = 0, j = 0, k = p; k <= r; k++)
{
if (i == n1)
a[k] = R[j++];
else if (j == n2)
a[k] = L[i++];
else if (L[i] <= R[j])
a[k] = L[i++];
else
{
a[k] = R[j++];
inversions += n1 - i;
}
}
return inversions;
}
void MergeSort(int *a, int p, int r)
{
if (p < r)
{
int inversions = 0;
int q = (p + r) / 2;
inversions += MergeSort(a, p, q);
inversions += MergeSort(a, q + 1, r);
inversions += Merge(a, p, q, r);
return inversions;
}
return 0;
}