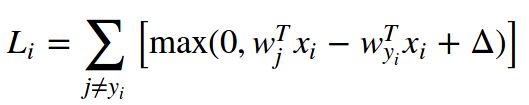本小节将讨论关于网络权值参数更新的集中常见的方法:
为什么要optimization
这样做的目的是为了找到最合适的W,使得loss function的值最小
为什么要用梯度下降方法
考虑平面中的两个点(A,B),几何上来说两点间直线距离最短,也就是说点A沿着A,B斜率方向走是最快的。对于多维度空间,每个维度的斜率组合成的向量称为梯度
怎么算梯度方向
以SVM的loss function为例,同时结合复合求导法则
y=z(x) -> y'=z'*x'( x'表示求导的意思)
因为我们的目标是想要对于某张照片 x_i(分类为y_i),其对种类y_i的打分能够向增加的方向走(使得loss变小),所以将w_yi看成是自变量,其余看成常数
那么假设有C类,其中k类的得分比y_i类得分低(假设delta=0),C-K-1类得分比y_i类要高
L=k*0+ (w_j_1*xi-W_yi*xi)+....+(w_j_c-k-1*xi-W_yi*xi)
以w_yi为自变量求导:
L'=(c-k-1)*(-xi)
也就是说梯度就是错误类得分比正确类高的 次数乘以输入xi
-> -a*xi就是梯度
所以利用微分方法求梯度就变得很简单了,只需要数出所有错误分类的个数,再乘以像素输入就是梯度方向了
应该向梯度方向前进多少合适(learning rate)
以上面的图来说明,其中蓝色越深的地方说明loss越小,越红表示loss越大
假设我们的W起始点在圆圈点,虚线的长度可以表示向梯度下降方向迈多大的步伐,极端情况下假如一步就直接迈到了虚线的最末端,那么可以想象收敛到loss最低点将会很困难
实际上这个步长就是学习率 (learning rate)
为什么要用到Mini-batch
特别要注意的是因为上面的x_i为1维的而且是针对W_yi求的偏导数,所以这个梯度实际上是关于W_yi的梯度。那么很显然如果我们需要对整个权重W进行梯度更新,就需要足够多的X(才有足够丰富的分类)作为输入才行。当然我们可以将整个训练集的图片输入进去来进行一次参数更新,但是很显然这样做使得一次参数更新的计算要很久,一般我们都会用一个小一点的batch作为输入来计算参数的更新(32,64,128,256等),这样做的好处:明显计算一次梯度的时间短很多
什么叫SGD(Stochastic Gradient Descent)
Even though SGD technically refers to using a single example at a time to evaluate the gradient, you will hear people use the term SGD even when referring to mini-batch gradient descent (i.e. mentions of MGD for “Minibatch Gradient Descent”, or BGD for “Batch gradient descent” are rare to see), where it is usually assumed that mini-batches are used.
严格意义上说SGD表示的是用一张图片(one example)来更新参数(但是实际上这样做效率很低没有人会这样做),人们提到SGD的时候一般是指用Mini-batch Gradient Desent
梯度更新的变种:Momentum update
Momentum update引入了动量的概念,其主要的想法是仿照 位移(参数),输入(参数更新),加速度(梯度)建立关系,使得不直接利用梯度来影响参数,而是加入了中间变量v
# Momentum update
v=momentum*v-learning_rate*dx # integrate velocity
x+=v# integrate position
其中dx表示梯度方向,momentum表示一个惯性系数(0~1),这个系数使得当梯度消失的时候速度v能够逐渐趋向于0,这样才能够停下来
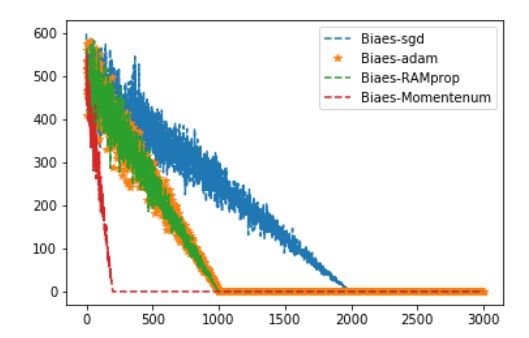
上面用一个简单的线性回归作为例子,可以看到Momentum的收敛速度很快(主要还是没有局部最优点)。一般神经网络的loss function都是 non-convex-function所以存在很多的局部最优点,SGD在这些局部最优点上会缓慢的震荡前进,使得收敛过程很漫长或者是不可能,Momentum可以理解成自带了惯性速度能够冲过这些局部最优点。
梯度更新的变种:Nesterov’s Accelerated Momentum (NAG)
NAG是Momentum update的变种,它收敛的速度更快而且对于比较大的momentum其表现更加的稳定
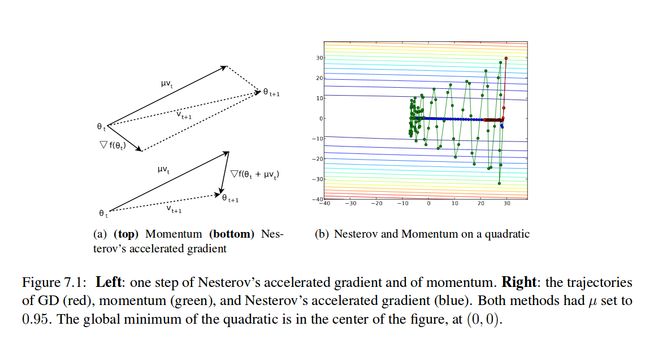
论文公式形式
代码形式:
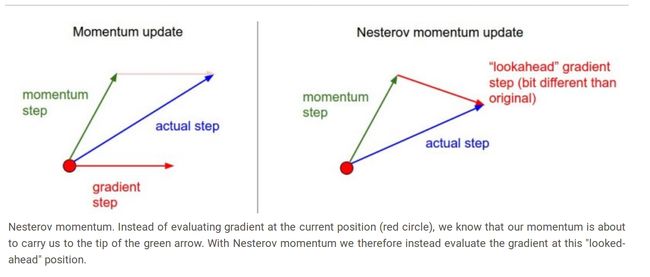
NAG与Momentum update的主要区别在于求梯度的顺序
m在更新速度v之前就求了梯度,而n是在将速度作用到参数x后再更新
这样做的好处是:
假如原来的惯性方向 :X+mu*v 对于参数更新有负面的影响,那么先将这个作用到参数后再求出来的偏导数将会有矫正这种影响的趋势
下面的图是两种方法更新梯度的示意图
左边表示momentum,因为其先求出梯度,再与原来的速度叠加得到新的前进方向(actual step)
右边表示NAG,其先叠加原来的速度来更新参数,再求参数的梯度,所以可以看到两种的梯度方向是不一样的(因为这样 'peek ahead'的方法)使得NAG收敛更加快而且更加平稳(没有那么震荡)
从右图可以看出NAG比momentum收敛速度更快,而且没有那么震荡
注意在tf里面NAG优化器是包含在MomentumOptimizer里面的
上面的方法都是固定了学习率(learning rate)条件下,采用各种各样的方法来利用梯度信息调整权值参数
下面的方法将尝试用浮动的学习率(learning rate)来更新参数
Adagrad 一种自适应学习率的梯度(?)更新方法
cache累加了每次梯度的平方,可以想象,在前几次更新中,cache的值很小,所以dx/(np.sqrt(cache)+eps) (注意这里的矩阵除法是值同维度的矩阵对应位置相除)相当于在增强梯度(类比于除一个小于1的数)
当迭代多次后,分母的矩阵的元素会比dx大很多,相当于对比较大的梯度进行缩减(大于1),对比较小的梯度增大(小于1)。实际上这样做相当于越到后面从本次梯度里面得到的信息越小(很少cache里面的元素小于1了,相当于一直在惩罚或者说是缩小梯度),这也是为什么说这样做的学习率(learning rate)是单调减的
这样做的主要缺点还是在DL中用固定的单调减learning rate会导致太快收敛
更新:根据下面参考的文章,从梯度矩阵的每一个元素来看,其更新的学习率是变化的,和其历史值的平方和累加成反比,可以想象,当这个值小于1的话对这个元素是增强的效果(实际上这个方法提出就是为了解决一些比较少出现的例子其权值更新太慢的问题)。但是到最后这个值很容易就大于1,使得对这个梯度元素变小,也就是对梯度越来越不敏感,直到最后停止学习
RMSprop
RMSprop 是上面Adagrad的改进,可以看到两者的第二个等式是相同的,只是第一个等式变成了滑动平均的形式。这样改进的主要好处是使得learning rate不再是单调减的,同时仍然能保证调整lr(把和dx所占的影响力的大小联系?)
Adam
Adam可以看做对RMSprop的进一步改进,其将梯度也进行了滑动平均(和前面的动量形式很相似)。也就是相对于Adagrad,Adam同时对cache和梯度进行了滑动平均
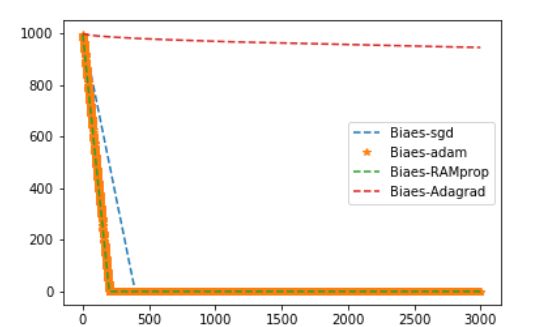
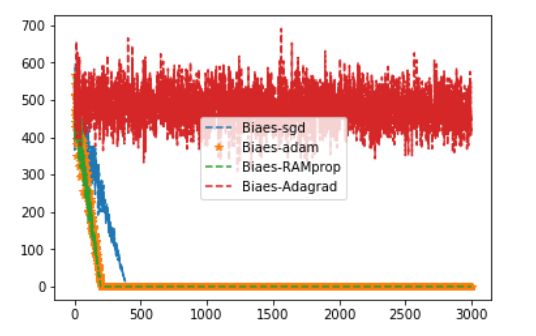
虽然在我的例子:预测一个固定的数中,Adagrad表现的最差。但是根据其他人的实验结果:Adagrad/Adadealta会更容易一些,因为不太依赖与lr的设定。当然对于精调的SGD+Momentum表现肯定更加好
In my own experience, Adagrad/Adadelta are "safer" because they don't depend so strongly on setting of learning rates (with Adadelta being slightly better), but well-tuned SGD+Momentum almost always converges faster and at better final values.
很系统的总结:
http://sebastianruder.com/optimizing-gradient-descent/
中文翻译:
http://blog.csdn.net/google19890102/article/details/69942970