title: 算法第四课
date: 2016-10-18 15:06:36
tags: 算法
thumbnail: http://img2.imgtn.bdimg.com/it/u=4054526222,762120886&fm=21&gp=0.jpg
深度和广度是什么
为什么叫做深度与广度优先呢,其实是针对图的遍历而言的,请看
使用深度优先来便利这个图(具体什么是图,可以去搜索一下图论中关于图的定义)的具体过程是,假设从左边的顶点开始,沿着当前定点的边,走到未访问过的顶点;当没有未访问过的顶点时,返回到上一个点,继续试探别的点(沿着某一条分支走到底,然后回朔,再沿着另一条进行同样的操作)。所有的顶点都走过了或者是提前符合我们的条件,遍历结束。
广度优先的思想是:首先以一个未被访问过的顶点作为起始顶点,访问其所有相邻的顶点,然后对每个相邻的定点,再访问他们相邻的未被访问过的点定点,直到所有的点都被访问或者提前符合我们的条件,遍历结束。
使用广度或者深度来遍历图,都会得到这个图的生成树,这个以后会提到。
城市地图
假期,小朋友A想去小朋友B家玩,怎么去呢?小朋友A用百度地图搜索除了到B家的最短路径。上边是城市的地图。
数据是这样给出的:
5 8
1 2 2
1 5 10
2 3 3
2 5 7
3 1 4
3 4 4
4 5 5
5 3 3
第一行表示有5个城市,8条公路,接下来8行,每行都是类似于a,b,c这样的数据,表示有一条路可以从城市a到b(单向),并且路程有c公里。即a,b,c仅仅表示有一条路可以从城市a到城市b。小朋友A家在1号城市,小朋友B家在5号城市。请求出最短路径。
已知,有5个城市,8条公路,我们用一个5*5的二维数组来存储这些信息。
+ 1 - 2 - 3 - 4 - 5
1 0 2 -1 -1 10
2 -1 0 3 -1 7
3 4 -1 0 4 -1
4 -1 -1 -1 0 5
5 -1 -1 3 -1 0
0表示自己到自己的距离,-1表示不可以到达,比如说 map[2][1] = -1意味着从城市2不能到达城市1,接下来我们就要寻找最短的距离了。我们一个一个找,你会发现之前写过这样的代码,对,在算法第三课种,迷宫就是这么想的。一个深度查找就可以知道了(我们来动手写一下代码):
#include
int min = 9999999;
int book[101];
int map[11][11];
int n; // 多少个城市
int m; // 多少条路
int des;
void dfs(int currentCity, int distance) {
// 如果当前走过的路,已经大于之前走过的路,直接返回,不需要继续了
if (distance > min) {
return;
}
if (currentCity == n) {
if (distance < min) {
min = distance;
}
return;
}
for (int i = 1; i <= n; i ++) {
if (map[currentCity][i] != -1 && book[i] == 0) {
book[i] = 1;
dfs(i, distance + map[currentCity][i]);
book[i] = 0;
}
}
return;
}
int main(int argc, const char * argv[]) {
// 初始化地图
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i ++) {
for (int j = 1; j <= n; j ++) {
if ( i == j ) {
map[i][j] = 0;
} else {
map[i][j] = -1;
}
}
}
// 初始化道路
int a, b, c;
for (int i = 1; i <= m; i ++) {
scanf("%d %d %d", &a, &b, &c);
map[a][b] = c;
}
book[1] = 1; // 从城市1出发
dfs(1, 0);
printf("%d", min);
}
上边的地图我们发现城市之间只是单向的通道,如果改为双向的呢?大家把上边的地图修改一下看看。还有,发现了么,我们写了好多代码都离不开book这个数组,嘿嘿。广度优先和深度优先该什么时候使用呢(所有周边的权值相同的时候使用广度,思考为什么)。
第四课其实是第三课的练习与只是的完善,但并不是,接下来我们来探讨最短路径问题:
最短路径
Floyd-Warshall
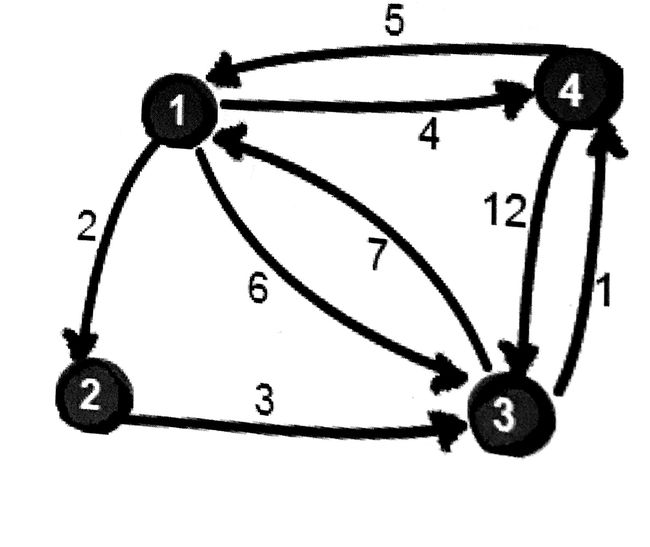
上图中,有4个城市,8条线路,公路上的数字表示这条公路的长短,请注意这些公路是单向的,我们现在需要求任意两个城市之间的最短路程,也就是求2个点之间的最短路径,这个问题也被称为多源最短路径问题。
现在需要一个数据结构来存储图的信息,依旧,跟以前一样,我们可以选择一个4*4的矩阵,比如1号城市到2号城市的距离为2,则设map[1][2]=2,2号城市无法到达4号城市,则设置距离为无穷大(之前我们用的是-1表示不可以到达),并约定一个城市自己到自己的路程为0。具体如下:
+ 1 2 3 4
1 0 2 6 4
2 / 0 3 /
3 7 / 0 1
4 5 / 12 0
通过之前的学习,我们可以使用深度或者广度优先搜索来寻找,即对每两个点都进行一次深度或者广度优先搜索,就可以求得结果,可是还有没有别的办法呢?
根据以往的经验,我们思考下,如果要让任意两点之间的距离变短,只能引入第三个点K,并通过这个点中转,A → K → B,才可能缩短A到B的路程,那么这个中转点是1~n种的哪个点呢?而且有的时候不仅仅通过1个点中转,甚至通过2个点中转可以得到最短的路程(在图上,大家自己比划一下)。将这个问题一般化:当任意两点之间不允许经过第三个点时,这些城市之间的最短路程就是初始路程,假设,目前只允许经过1号顶点,求任意两点(i,j)之间的最短距离,该如何求呢?只需判断
map[i][1] + map[1][j] < map[i][j]
这样,map[i][1]表示i点到1点的路程,map[1][j]表示从1号顶点到j点的路程。这样,i,j是不定的,我们要确认所有的2点之间的最短路程,所以i,j都是1~n循环:
for (int i = 1; i <= 4; i ++) {
for (int j = 1; j <=4; j ++) {
if (map[i][1] + map[1][j] < map[i][j]) {
map[i][j] = map[i][1] + map[1][j];
}
}
}
这样我们简单的算出了,只中转1号顶点,任意两点间的最短距离。同理,经过别的顶点都是一样的,所以,经过所有的顶点中转:
for (int k = 0; k <= 4; k ++) {
for (int i = 1; i <= 4; i ++) {
for (int j = 1; j <=4; j ++) {
if (map[i][k] + map[k][j] < map[i][j]) {
map[i][j] = map[i][k] + map[k][j];
}
}
}
}
对你没看错,就是这样么简单,这种思想也被称为动态规划。核心代码只有5行,不过,它的时间复杂度为:
O(N^3)
但是要注意,这种算法不能解决包含
负权回路的图,自行科普一下什么叫做负权环。算了,因为带有负权环的图没有最短路径,查了之后思考一下。
如果对时间要求不高,使用这种方法可谓最容易了,当然还有更快的算法:
Dijkstra
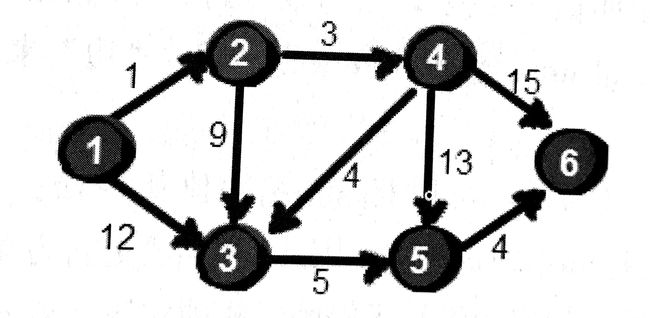
上节我们说的是多源最短路径问题,任意的两个点,这次呢,我们来解决确定一个顶点,到其他各个顶点的最短路径,也称为单源最短路径问题,先来看一下图:
如上图,我们求一下,从1号定点,到达其余各个点的最短路程,与之前的算法一样,我们使用二维数组来表示这些点之间的路程:
+ 1 2 3 4 5 6
1 0 1 12 / / /
2 / 0 9 3 / /
3 / / 0 / 5 /
4 / / 4 0 13 15
5 / / / / 0 4
6 / / / / / 0
还需使用一个一维数组来存储1号顶点到其余点的路程,并将此时数组种的值描述为估计值:
顶点: 1 2 3 4 5 6
距离: 0 1 12 / / /
既然是求1号顶点到其余各个点的值,那就先找一个离1号点最近的点,也就是2号点,这个时候,2号点的值从估计值变为确定值,即1号顶点到2号顶点的最短路径就是当前数组中的值。
为什么?因为1号点的周围,除了2号点,别的点都要远,所以选择2号点作为接下来的中转点没问题吧?
接着想,看上图,通过2号点,我们可以到达3号和4号,所以接下来我们要想的是,2到3能否让1到3更小。上边的数组我们用distance命名,即比较,distance[3]和distance[2]+map[2][3]的大小。distance[2]大家还记吧,表示点1到点2的路程,map[2][3]表示点2到点3的路程。我们发现,distance[3] > distance[2]+map[2][3],所以把distance[3]的值更新为10,这个过程,有个专业的术语,叫做松弛,1号到3号点的路程,通过2号到3号边松弛成功,这就是Dijkstra算法的主要思想:通过边来松弛1号点到其余点的路程。同理,对2号到4号点的距离可以松弛为distance[2]+map[2][4] ,所以把distance[4]改为4。2号所有的边都松弛结束后:
顶点: 1 2 3 4 5 6
距离: 0 1 10 4 / /
接下来在剩下的3、4、5、6点中,选出距离1号最近的点,为4号点,然后对4号点的所有出边进行松弛(4到3,4到5,4到6)(为什么?我们确定了点1,点2,所以在松弛点4周边的时候,前面的线路就是1-2-4 然后到3,到5,到6):
顶点: 1 2 3 4 5 6
距离: 0 1 8 4 17 19
接着在余下的3、5、6中选择最近的点3进行松弛(3到5)(点1,点2,点4,点3确定,所以接下来是1-2-4-3-5):
顶点: 1 2 3 4 5 6
距离: 0 1 8 4 13 19
继续在余下的5、6点种对点5进行松弛(1-2-4-3-5)(5到6):
顶点: 1 2 3 4 5 6
距离: 0 1 8 4 13 17
现在,我们已经确定了所有的距离,简单不。我们用代码实现上述的思路:
int main(int argc, const char * argv[]) {
int map[10][10], distance[10], book[10];
int UNACCESS_DISTANCE = 999999;
int n, m; // N表示点的个数,M表示边的条数
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i ++) {
for (int j = 1; j <= n; j ++) {
if ( i == j ) {
map[i][j] = 0;
} else {
map[i][j] = UNACCESS_DISTANCE;
}
}
}
// 读入边
for (int i = 1; i <= m; i ++) {
int tx, ty, td;
scanf("%d %d %d", &tx, &ty, &td);
map[tx][ty] = td;
}
// 初始化distance数组,这里是1号顶点到其余点的初始路程
for (int i = 1; i <= n; i ++) {
distance[i] = map[1][i];
}
// 标记数组初始化
for (int i = 1; i <= n; i ++) {
book[i] = 0; // 全部未定值
}
book[1] = 1; // 我们通过把book置为1表示该点已经确定值。
// 核心算法
int min = UNACCESS_DISTANCE;
int fixedValue = 0; // 定值
for (int i = 1; i <= n - 1; i ++) { // 点1定了,所以少循环一次就够了
// 找到距离1号的最近的点
for (int j = 1; j <= n; j ++) {
if (book[j] == 0 && distance[j] < min) {
min = distance[j];
fixedValue = j;
}
}
book[fixedValue] = 1;
min = UNACCESS_DISTANCE; // 归位寻找最小值
for (int k = 1; k <= n; k ++) {
if ( map[fixedValue][k] < UNACCESS_DISTANCE ) { // 是可以连通的
if ( distance[fixedValue] + map[fixedValue][k] < distance[k] ) { // 按照思路比较
distance[k] = distance[fixedValue] + map[fixedValue][k];
}
}
}
}
for (int i = 1; i <= n; i ++) {
printf("到%d点%d ", i, distance[i]);
}
}
通过上述的代码,我们可以看出,时间复杂度为:
O(N^2)
这里其实还可以优化,我们以后也会提到。另外,对于边数少于N^2的稀疏图来说M远远小于N*N的图,M相对大的图,叫做稠密图,我们可以使用邻接表(等下会说)来代替邻接矩阵,使得整个时间复杂度优化到:
O(M+N)logN
最快的情况,就是M=N^2,这个时候,(M+N)logN要比N*N还大。但是大多数情况下,边不会有那么多。接下来我们主要讲解邻接表,先看数据
4 5
1 4 9
4 3 8
1 2 5
2 4 6
1 3 7
第一行表示顶点个数与边数,接下来的每行,表示x到y的路程为z。现在要使用邻接表来存储这个图,先给出代码如下:
int main(int argc, const char * argv[]) {
int n, m; // 点、边
// u、v、w数组的大小,要根据实际情况来设置,一般要比m大1
int u[6], v[6], w[6];
// first和next数组要比n大1
int first[5], next[5];
scanf("%d %d", &n, &m);
// 初始化first数组1~n的值为-1,表示1~n顶点暂时没有边
for (int i = 1; i <= n; i ++) {
first[i] = -1;
}
for (int i = 1; i <= m; i ++) {
scanf("%d %d %d", &u[i], &v[i], &w[i]); // 读入每条边
// 重点操作
next[i] = first[u[i]];
first[u[i]] = i;
}
}
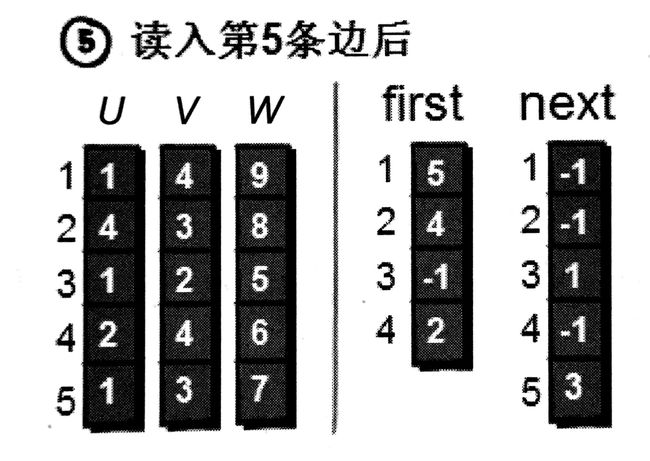
这里展示的是使用数组来实现邻接表,首先我们为每一条边进行1~m的编号,用u、v、w三个数组来记录每条边的信息,即第i条边用u[i],v[i]->w[i]来表示,first数组的1->n分别用来存储1->n号点的第一条边的编号,即first[u[i]]保存点u[i]的第一条边的编号,next[i]存储编号为i的边的下一条边的编号。
接下来如何遍每一条边呢?我们之前说过,其实first数组存着每个顶点i的第一条边,比如1号点的第一条边是编号为5的边(1,3,7),2号点的第一条边是编号为4的边(2,4,6),3号点没有出向边,4号点的第一条边是编号为2的边(4,3,8)。那么如何遍历1号点的每一条边呢?在找到1号点的第一条边后,剩下的都可以在next数组中依次找到:
int k = first[1];
while (k != -1) {
printf("%d %d %d\n", u[k], v[k], w[k]);
k = next[k];
}
输出了
1 3 7
1 2 5
1 4 9
细心的人会发现,此时遍历某个点的边的时候的遍历顺序,正好与读入的时候顺序相反,因为在每个点插入边的时候,都是直接插入表的首部而不是尾部,不过这并不会产生任何问题,这恰好是奇妙之处。遍历每个定点的边:
for (int i = 1; i <= n; i ++) {
int k = first[i];
while (k != -1) {
printf("%d %d %d\n", u[k], v[k], w[k]);
k = next[k];
}
}
可以发现,使用邻接表存储图的时候,时间空间复杂度是
O(M)
遍历一条边的时间复杂度也是同样的,如果一张图是稀疏图的话,选用邻接表来存储要比使用矩阵好的多。
Dijkstra算法虽然不错,但是依旧无法解决负权边(哈哈,就是有边的路程是负数)的图,所以我们引出一个无论是思想上还是代码实现上都堪称完美的最短路径算法:
Bellman-Ford
算法极其简单,核心的代码只有4行,我们先来看看它的样子:
for (int k = 1; k <= n - 1; k ++) {
for (int i = 1; i <= m; i ++) {
if (distance[v[i]] > distance[u[i]] + w[i]) {
distance[v[i]] = distance[u[i]] + w[i];
}
}
}
上边的代码中,外层循环一共循环了n-1次,内部循环循环了M次,即枚举每一条边,distance数组的作用与Dijkstra算法一样,记录源点到各个点的最短路径,u、v、w三个数组用来记录边的信息。
if (distance[v[i]] > distance[u[i]] + w[i]) {
distance[v[i]] = distance[u[i]] + w[i];
}
上面这行代码的意思是,看看能否通过u[i]->v[i](值为w[i])这条边,使得1号点到v[i]号顶点的距离变短。即1号点到u[i]号点的距离加上u[i]->v[i]这条边的值,是否会比原先1号点到v[i]号点的距离dis[v[i]]要小,这一点与松弛的操作是一样的,现在我们要把所有的边都松弛一遍:
for (int i = 1; i <= m; i ++) {
if (distance[v[i]] > distance[u[i]] + w[i]) {
distance[v[i]] = distance[u[i]] + w[i];
}
}
把每条边松弛一遍后,会有什么效果呢?我们来看个具体的例子,求下图1号点到其余所有点的最短路径。
我们还是使用一个distance数组来存储1号点到所有点的距离:
position: 1 2 3 4 5
distance: 0 / / / /
我们开始对每一次输入的边进行松弛:
首先输入了2,3,2,所以就是对2->3这条边松弛,即判断distance[3]>distance[2]+2?此时,2与3都是未知,所以无穷大与无穷大+2不可以做比较,所以2->3松弛失败,接着对第二个输入1,2,-3进行松弛,即判断distance[2]>distance[1]+(-3),distance[1]是0,所以distance[2]为无穷大,大于-3,所遇distance[2] = -3,依次对每组输入的数字进行松弛,得到
position: 1 2 3 4 5
distance: 0 -3 / / 5
我们发现,对每条边松弛之后,distance[2]与distance[5]的值变小。即1号点到2号与5号的路程都变小了。接下来我们对所有的边进行下一轮松弛:
过程与上一轮一样(过程依旧是从第一组输入的边开始,大家脑补),结果为:
position: 1 2 3 4 5
distance: 0 -3 -1 2 5
在这一轮松弛后,我们发现,现在通过2 3 2这条边,可以使1号点到3号点的具体变短。实际上,第一轮松弛过后,得到的是从1号点只能经过一条边到达其余各点的最短路径长度。第二轮松弛过后,得到的是从1号点最多经过2条边到达各个点的最短路径长度,当然K轮就是K条边。现在有一个新的问题了,K是多少?多少轮可以让我们求得答案呢?
只需要进行n-1轮就够了,因为在一个含有n个定点的图中,任意两点之间的最短路径最多包含n-1边。有人要问了,不是还有回路么?答案是,不可能,最短路径肯定是一个不包含回路的路径,假设有负数路程,那么每走一次就会减少一次,很明显不可能的。接下来,我们完成上边的后2轮松弛,第三轮过后:
position: 1 2 3 4 5
distance: 0 -3 -1 2 4
第四轮后:
position: 1 2 3 4 5
distance: 0 -3 -1 2 4
最后,说白了,这个算法就是,对所有输入的边,进行最多n-1次松弛,但是我们会发现,我们在想的时候,一些已经确定的点,我们还是想了一下对他松弛的过程,是不是有些浪费呢?先来看完整的代码:
int main(int argc, const char * argv[]) {
int n, m; // 点、边
int distance[10]; // 用来存放源距各个点的路程
int u[10], v[10], w[10]; // u -> v 的路程是 w
int UNACCESS_VALUE = 999999; // 模拟正无穷大
scanf("%d %d", &n, &m);
for (int i = 1; i <= m; i ++) {
scanf("%d %d %d", &u[i], &v[i], &w[i]);
}
// 初始化路程数组
for (int i = 1; i <= n; i ++) {
distance[i] = UNACCESS_VALUE;
}
distance[1] = 0;
// 核心算法
for (int i = 1; i <= n - 1; i ++) {
for (int j = 1; j <= m; j ++) {
// 按照刚刚的思想去写代码:源到目的地的距离 > 源到起点的距离 + 起点到目的地的距离
if ( distance[v[j]] > distance[u[j]] + w[j] ) {
distance[v[j]] = distance[u[j]] + w[j];
}
}
}
for (int i = 1; i <= n; i ++) {
printf("%d ", distance[i]);
}
}
此外,这个算法还可以判断一个图是否有负权回路,如果在n-1轮后,依然存在
if ( distance[v[j]] > distance[u[j]] + w[j] ) {
distance[v[j]] = distance[u[j]] + w[j];
}
意味着,n-1轮松弛后,还可以继续松弛,说明有负权回路。这个算法的时间复杂度为:
O(M*N)
这个时间复杂度貌似高于Dijkstra算法,我们还可以继续对它进行优化。在实际操作中(上边的例子也是),其实不需要n-1次就能算出最短路径,我们也说过,最多使用n-1次,所以我们可以添加一个变量,用来标记数组distance是否在本轮松弛中发生了变化,如果没有发生变化就提前跳出循环。
int check = 0;
for (int i = 1; i <= n - 1; i ++) {
check = 0; // 标记本轮松弛是否会发生
for (int j = 1; j <= m; j ++) {
if ( distance[v[j]] > distance[u[j]] + w[j] ) {
distance[v[j]] = distance[u[j]] + w[j];
check = 1;
}
}
if ( check == 0 ) {
break;
}
}
刚才我们也提到过,其实一些已经松弛成功的边还在被无用的松弛,所以我们继续优化,每次只对最短路径估计值发生了变化的点的所有出边进行松弛,我们称为Bellman-Ford的队列优化。
每次选取队首点u,对点u的所有出边进行松弛操作,例如有一条u到v的边,如果通过n到v这条边使源点到点v的路程变短,而且点v不在当前的队列中,就将点v放入队尾。需要注意的是,同一个点同时在队列中出现多次是毫无意义的,所以我们需要一个数组来进行去重。在对点u的所有出边松弛完毕后,将u出队。反复操作至队列为空。我们用代码来讲解:
int main(int argc, const char * argv[]) {
// 还记得之前讲到的邻接表么?这里我们使用邻接表来存储数据
int n, m;
// first 比n大1 next比m大1
int first[6], next[8];
int u[8], v[8], w[8];
int distance[8];
int book[6];
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i ++) {
first[i] = -1; // 初始化first数组,都暂时无边
book[i] = 0; // 初始化标记数组,都不在队列中
}
for (int i = 1; i <= m; i ++) {
scanf("%d %d %d", &u[i], &v[i], &w[i]);
// 建立邻接表的关联
next[i] = first[u[i]];
first[u[i]] = i;
}
// 初始化初始路程
for (int i = 1; i <= n; i ++) {
distance[i] = 999999;
}
distance[1] = 0;
// 创建队列
int queue[101] = {0}, head = 1, tail = 1;
// 将1号顶点入队
queue[tail] = 1;
tail ++;
// 标记这个点已经在队列中
book[1] = 1;
int k = 0;
while (head < tail) { // 将n-1的循环改为队列循环
// 邻接表的遍历方式
k = first[queue[head]];
while (k != -1) {
// 是否可以松弛
if ( distance[v[k]] > distance[u[k]] + w[k] ) {
distance[v[k]] = distance[u[k]] + w[k];
// 松弛成功,当前成功松弛的点是 v[k].
// 入队,检查标记
if (book[v[k]] == 0) {
queue[tail] = v[k];
tail ++;
book[v[k]] = 1;
}
}
k = next[k];
}
// 对首已经松弛结束了,置为0,因为本次可能不是松弛的最终结果
book[queue[head]] = 0;
head ++;
}
for (int i = 1; i <= n; i ++) {
printf("%d ", distance[i]);
}
return 0;
}
检查一个数字是否在队列中也可以遍历,但是时间复杂度是O(N),但是使用book就变成了O(1)。并且,如果一个点,进入到队列的次数超出n次,这图也存在负权回路。
至此,最短路径算法告一段落了,以后有优化我们再提起。