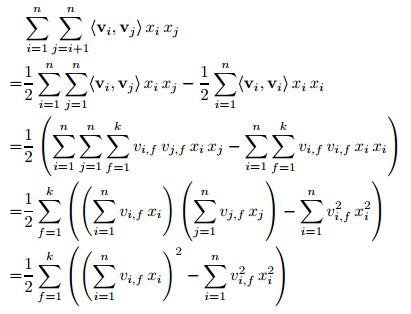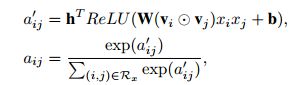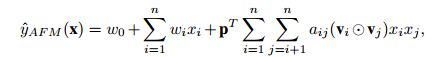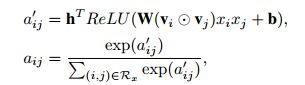1、FM回顾
1.1 引言
FM是一种监督学习,在线性单特征模型中加入了二阶特征交互,但是两两特征交互有个明显的缺点就是所有交互特征的权重都是相同的,显而易见,不同特征的重要性是不同的,比如女性-篮球和男性-篮球,其交互的权重肯定是不一样的,显然FM模型并没有考虑到这一点。
因此在AFM模型中引入了交叉项的权重,不同的特征交叉项,由于影响的效果不同,所以这个权重也不同,文章中把这个权重称为注意力权重。但是AFM有个很大的不足就是参数过于多,计算量非常大。
1.2 FM公式
其二阶second-order项简化公式为:
由公式可以看出,若embedding_size也就是最外层的求和不考虑的话,那二阶交叉项得到的就是一个k维的矩阵,这个k维的矩阵输入DNN中就可以进行模型的变换,这个矩阵下边就记为[k]。
| 模型 | 结构 | 与DNN结合 |
|---|---|---|
| DeepFM | 并行结构 | [k]直接输入DNN中,与FM公式进行concat,相当于FM二阶后再加入高阶特征 |
| FNN | 串行结构 | 非end-to-end模型,把一次项二次项权重w,v预训练好,而后输入DNN中 |
| FNM | 串行结构 | [k]直接输入DNN中,替换FM公式中的二阶交互项 |
| AFM | 串行结构 | 在二次项交互权重之上再加入了注意力权重系数,替换原始的二次项 |
2 AFM结构
2.1 AFM原理
因为二阶交互项的重要性不同,因此在交互项之前加入了一个注意力因子,这个注意力因子就表示交互项的重要程度。这个就是Attention机制
FM的二阶项表达:
AFM的二次项表达
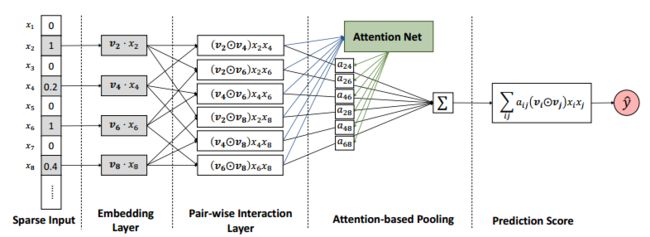
2.2 AFM结构
上图就是AFM二次交叉项的结构图,其忽略了一次项和偏置的部分,前三部分就是FM的二次项部分,后边加入的注意力网络attention-based pooling才是本文的创新和核心,文中加入一个attention net生成注意力权重参数,加入二次项交叉项之前,而且直接对二次项特征维度进行累加,生成加权和。
2.2.1
attention net网络的表示公式,求得其交互项的注意力权重,因为权重系数表示的是交叉项的相关程度,因此a的系数表示越大表示其相关程度越高,a系数的综合为1,因此设计一个注意力机制网络,而后通过softmax函数,求出系数的值。
得到注意力权重后, 对FM的表达式进行改写为:
其中权重,,,,k为embedding后的向量的维度,t为attention network的隐藏维度。
由公式可以看出,AFM在FM的基础上只是加入了注意力机制,并没有使用DNN的网络结构进行非线性的学习其他高阶特征。
3、实验代码
实验过程中还是使用了自己的数据集,特征数量feature_size将近3w,field_size为69,因此其交互项为69*68/2=2346个。根据之前NFM的代码进行改写,loss函数为MSE,使用Adam作为优化,同样采用了RMSE进行评分预测:
3.1数据预处理
def get_feature_dict(df,num_col):
'''
特征向量字典,其格式为{field:{特征:编号}}
:param df:
:return: {field:{特征:编号}}
'''
feature_dict={}
total_feature=0
df.drop('rate',axis=1,inplace=True)
for col in df.columns:
if col in num_col:
feature_dict[col]=total_feature
total_feature += 1
else:
unique_feature = df[col].unique()
feature_dict[col]=dict(zip(unique_feature,range(total_feature,total_feature+len(unique_feature))))
total_feature += len(unique_feature)
return feature_dict,total_feature
def get_data(df,feature_dict):
'''
:param df:
:return:
'''
y = df[['rate']].values
dd = df.drop('rate',axis=1)
df_index = dd.copy()
df_value = dd.copy()
for col in df_index.columns:
if col in num_col:
df_index[col] = feature_dict[col]
else:
df_index[col] = df_index[col].map(feature_dict[col])
df_value[col] = 1.0
xi=df_index.values.tolist()
xv=df_value.values.tolist()
return xi,xv,y
3.2 AFM模型
3.2.1 设置权重初始化
权重的设置分为FM部分权重和attention部分的权重
#FM权重
w_0 = tf.Variable(tf.constant(0.1),name='bias')
w = tf.Variable(tf.random.normal([feature_size, 1], mean=0, stddev=0.01),name='first_weight')
v = tf.Variable(tf.random.normal([feature_size, embedding_size], mean=0, stddev=0.01),name='second_weight')
3.2.2 embedding层和placeholder的设置
feat_index = tf.compat.v1.placeholder(tf.int32,[None,None],name='feat_index')
feat_value = tf.compat.v1.placeholder(tf.float32,[None,None],name='feat_value')
label = tf.compat.v1.placeholder(tf.float32,shape=[None,1],name='label')
embedding_first =tf.nn.embedding_lookup(w,feat_index) #None*F *1 F是field_size大小,也就是不同域的个数
embedding = tf.nn.embedding_lookup(v,feat_index) #None * F * embedding_size
feat_val = tf.reshape(feat_value,[-1,field_size,1])
#vx的计算
embedding_vx = tf.multiply(embedding_first,feat_val)
3.2.2 模型的设置
1)线性部分
y_first_order= tf.reduce_sum(embedding_vx,2) # None*F
y_first_order_num = tf.reduce_sum(y_first_order,1,keepdims=True) # None*1
liner = tf.add(y_first_order_num, w_0) # None*1
2)attention部分
(a)attention权重初始化(K为embedding_size,A为attention_size)
公式中:
W的权重维度为 K * A
b的权重维度为 1* K
h的权重维度为 1* K
p的权重维度为 1* K
#Attention部分的权重
weights={}
glorot = np.sqrt(2.0 / (attention_size + embedding_size))
weights['attention_w'] = tf.Variable(
np.random.normal(loc=0, scale=glorot, size=(embedding_size,attention_size)), dtype=np.float32
)
weights['attention_b'] = tf.Variable(
np.random.normal(loc=0, scale=glorot, size=(attention_size,)), dtype=np.float32
)
weights['attention_h'] = tf.Variable(
np.random.normal(loc=0, scale=glorot, size=(attention_size,)), dtype=np.float32
)
weights['attention_p'] = tf.Variable(
np.random.normal(loc=0, scale=glorot, size=(embedding_size,)), dtype=np.float32
)
(b) Attention Net
按照公式来计算注意力权重
为了得到每一个两两交叉项的向量,也就是求得
交叉项的embedding,我们写了个循环,如下边代码,通过stack使之变成一个张量,而后通过第一维和第二维的转置得到一个None* F(F-1)/2* K维的张量。 F(F-1)/2* K表示一个样本所有交互项的交互矩阵。
# 交互项的矩阵 #None*F(F-1)/2*k
attention_weight_list=[]
for i in range(field_size):
for j in range(i+1,field_size):
attention_weight_list.append(tf.multiply(embedding_vx[:,i,:],embedding_vx[:,j,:]))
attention_cross = tf.stack(attention_weight_list)
attention_cross = tf.transpose(attention_cross,perm=[1,0,2],name='transpose') #None*F(F-1)/2*k
得到了attention_cross交互矩阵后,根据公式:
计算权重系数,使用softmax把权重系数总和限制为1,其最后输出矩阵大小为None* F(F-1)/2* 1
# 可以带入权重attention
attention_weight = tf.add(tf.matmul(attention_cross,weights['attention_w']),weights['attention_b']) #None*F(F-1)/2*A
attention_weight_a = tf.reduce_sum(tf.multiply(tf.nn.relu(attention_weight),weights['attention_h']),axis=2) #None*F(F-1)/2
attention_weight_out = tf.reshape(softmax(attention_weight_a),[-1,int(field_size*(field_size-1)/2),1]) #None*F(F-1)/2*1
(softmax的函数)
def softmax(x):
if len(x.shape) > 1:
fenzi_exp= tf.exp(x - tf.reduce_max(x))
fenmu = 1.0/tf.reduce_sum(fenzi_exp,axis=1,keepdims=True)
result = fenzi_exp * fenmu
else:
result = tf.exp(x - tf.reduce_max(x))/tf.reduce_sum(tf.exp(x - tf.reduce_max(x)))
return result
(c)二次项
#二阶second_order的输出
#所有交叉项相加
atten_add = tf.reduce_sum(tf.multiply(attention_cross,attention_weight_out),axis=1) #N*K
second_order = tf.reduce_sum(tf.multiply(atten_add,weights['attention_p']),axis=1,keepdims=True) #N*1
3)输出和优化
out = tf.add(liner,second_order) #N*1
#loss
loss = tf.nn.l2_loss(tf.subtract(out,label))
optimizer = tf.compat.v1.train.AdamOptimizer(lr,beta1=0.9,beta2=0.999,epsilon=1e-8).minimize(loss)
完整代码见:https://github.com/garfieldsun/recsys/tree/master/AFM
参考博客:
1、论文
2、https://www.jianshu.com/p/83d3b2a1e55d