平面波动方程实现线条波动效果

前两天看到一个水波的动画图，形如下面这样子，突然波动方程在记忆深处就复活了。发现这个方程可以很好玩，虽然只是二维的，但还是分享给大家。

waveWater.gif

* 波动方程的推导

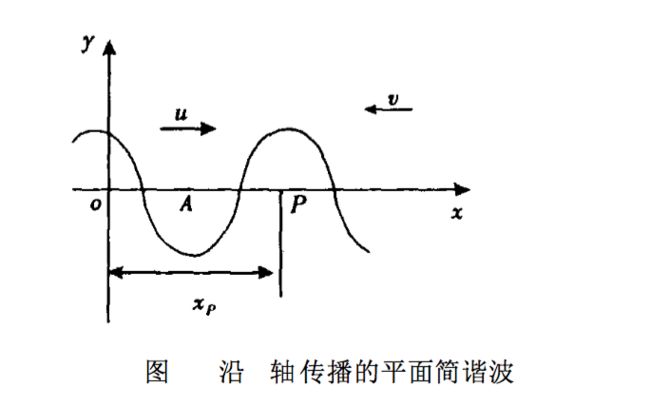
已知波源A的振动方程：y=Acos(ωt+φA⁡)。假设波沿x轴正方向传播速率记为u,沿x轴负方向传播速率记为V。以O点为坐标原点，A点的坐标为Xa，以水平向右为x轴的正方向建立坐标系。
当波沿x轴正方向传播的时候，如下图所示，在x轴正方向上任取一点P，与o点相距Xp。当得波向右传播时，P点的振动落后于A点，落后的相位为ω (Xp-Xa)/u。可得P点在任意时刻t的位移：y=Acos[ωt-ω (Xp-Xa)/u+φa]= Acos[ωt- ω Xp/u+(φa+ ω Xa/u)]。可参考:如何求解平面简谐波的波动方程。

沿x轴方向传播的平面简谐波

得到的这个方程叫平面简谐波动方程，形如：

y=Acos[ωt- ω Xp/u+(φa+ ω Xa/u)]

它能描述任意时刻任意点在Y轴方向上的位移y。加上一个微分的思想，取一个X+dx值,然后计算出对应的y值，将这些n个y值连成一条线就是任意时刻的波形图。当t在流逝的时候这个波形图不断的在重画，就形成了一个波动图了！在代码前先分析一下这个方程：y=Acos[ωt- ω Xp/u+(φa+ ω Xa/u)]

* 方程的物理意义

• y是y坐标的位置，也就是我们要计算点的y值
• A是振幅，就这个波振动幅度的大小
• ω是频率，可以理解为是振动的快慢，ω ＝ 2 / T（T是周期）
• t就是时间了，时间是均匀（绝对时空观）往前走的
• u描述的是波的传播速率，波速＝波长/周期
• φa描述的波源的初相位，在图上看就是这个点是在x轴（φa＝0）上开始振动，还是在x轴上多少或下多少（cosφa）的地方开始振动。

只是为了实现这种效果，我们就利用最简单的简谐波了。此时：

• 波的初相为φa ＝ 0
• 波源就在Xa处，即Xa ＝ 0

此时波动方程就变成了:

* 最简方程

y=Acos(ωt- ω Xp/u)

是不是简单了好多！这样再设两个变量，一个是周期T和波长K，根据 “波速＝波长/周期(u = K / T)” 和 ω ＝ 2π / T。波动方程就可以推导成这个：

y = Acos2π(t/T - Xp/K)

这样代码的样子就出来了，忍不住开始代码了吧！

*代码实现

利用Quartz2D就可以简单实现，用一个UIView来实现，命名为WaveView（所有代码都在WaveView.m文件里面）。
设置波的基本属性：

    @interface WaveView ()
{
    CGFloat screenWidth;
    
    float A;    // 振幅
    float t;    // 时间变量
    
    float T;    // 周期
    float K;    // 波长
}
@end

在init方法里面初始化波的基本属性值：

- (id)initWithFrame:(CGRect)frame
{
    self = [super initWithFrame:frame];
    if (self) {
        
        // 设置波的基本属性（）
        A = 6;
        t = 0;
        T = 1.0;
        K = 80;
        
        [self setBackgroundColor:[UIColor clearColor]];
        
        // 设置刷新图像的频率，0.3秒人眼就很难分辨出来了
        [NSTimer scheduledTimerWithTimeInterval:0.03 target:self selector:@selector(animateWave) userInfo:nil repeats:YES];
    }
    return self;
}

启动动画：

-(void)animateWave
{
    // 这里是时间机器，如果和刷新图像的时间间隔一样，那么就是正常时间的速度
    // 如果大于刷新时间间隔，那么时间就走的很快，是平常的多少倍自己去计算
    // 如果小于刷新时间间隔，那么时间就走的慢
    
    t+=0.05; // 这里比实际时间快
    
    [self setNeedsDisplay];
    

动画算法的实现：

- (void)drawRect:(CGRect)rect
{
    CGContextRef context = UIGraphicsGetCurrentContext();
    CGMutablePathRef path = CGPathCreateMutable();
    CGContextSetLineWidth(context, 2);
    CGContextSetStrokeColorWithColor(context, [[UIColor blackColor] CGColor]);
    float y=axleXOnScreenHeight;
    CGPathMoveToPoint(path, NULL, 0, y);
    
    // 这是将x轴微分单位为1pt，就是每隔1pt计算一个y值，将所有的y值连起来就是一个波图
    // 可以将微分单位设置大一点，有不一样的效果
    // y 值的计算就用推导出来的公式：y = Acos2π(t/T - Xp/K)
    for(float x=0;x <= screenWidth;x+=1){
        y =  A * cos(2*M_PI * (t / T -  x / K)) + axleXOnScreenHeight;
        CGPathAddLineToPoint(path, nil, x, y);
    }
    
    CGContextAddPath(context, path);
    CGContextDrawPath(context, kCGPathStroke);
    CGPathRelease(path);
}

效果如下，波长为80，屏幕宽了375刚好5个波峰的样子：

waveView.gif

其它好玩的效果(比如波动过程中改变振幅的大小，就可以增加波的节奏感等)：

waveViewZheXian.gif

waveViewWater.gif

waveViewUnkown.gif

是不是挺好玩的，可惜没有接触过3D引擎，不然整个世界都可以波动起来。
赶紧试试!
源码位置: https://github.com/stoull/Wave