用计算机教孩子真正的数学

最近观看到一场很好的TED演讲《Teaching kids real math with computers》，用计算机教孩子真正的数学。演讲抨击了现在主流的数学教育方法，孩子在学校里努力学习计算方法，但是对数学科学本身确很少掌握。演讲提出了用计算机代替数学计算过程，着重培养孩子的数学思维。演讲内容可以在 https://www.ted.com/talks/conrad_wolfram_teaching_kids_real_math_with_computers 观看，优酷上也有对应的英文字幕版：https://v.youku.com/v_show/id_XMzE1NzI4Njk2.html?spm=a2h0k.11417342.soresults.dtitle&debug=flv

下面是演讲的文字内容：

目前我们的数学教育面临着实际的问题。 基本上，没有人感到很满意。 那些学习数学的学生 觉得所学的知识与实际无关， 无趣以及困难重重。 那些运用数学的人们 又觉得他们所学的知识不够。 政府觉察到这是一个涉及到我们经济发展的大问题， 但他们却无从下手。 而老师们也感到很沮丧。 但是现在的数学 比人类历史上任何时间都更为重要。 一方面我们逐渐丧失 对数学教学的兴趣， 另一方面，我们的世界却比以前 更加趋向于数学化、数量化的数形世界中。

那么问题到底出在哪里，为什么产生了这样的分歧？ 我们该怎么解决这个问题？ 我想，答案就在 我们眼前。 使用计算机。 我相信 恰当地使用计算机 是使数学教育变得有效的 一剂良方。 在解释之前， 让我简要对比一下我们现实世界中的数学 和教学中的数学。 现实世界中 数学并不是数学家的专用品。 地质学家、 工程师、生物学家 等各行各业 都可能运用数学进行数模和模拟。 数学的应用实际上是非常广泛。 然而，教学中的数学则完全不同-- 它带有很多愚蠢的问题，大量的运算-- 还多数是人工笔头运算。 许多看起来很简单的， 不及现实世界中复杂的问题， 在学习的过程中都变得很困难。 关于数学的另一点就在于 数学有时看起来很“数学” 就像这个例子-- 不过有时又不像-- 比如说“我醉了吗？”

我们退一步再来看看， 我们为什么要教数学呢？ 教数学有什么意义呢？ 尤其是，为什么我们要将数学作为通识基础教育呢？ 为什么数学是教育的一个重要组成部分呢？ 为什么要作为必修课呢？ 我想，这大概有以下三个理由： 一是完成技术工作。 这对我们经济的发展至关重要， 就是我所说的日常生活。 二，要在今天的世界运作， 你就必须比几年前掌握 更多数学知识。 你需要去算你的房贷， 对政府的数据等种种数字保持怀疑。 第三，我把它称作 逻辑思维训练，逻辑思维。 这几年 我们努力使社会运作和思维 都变得符合逻辑，并将这做为人类社会的一部分。 必须要指出 数学正是实现这种构想的重要工具。

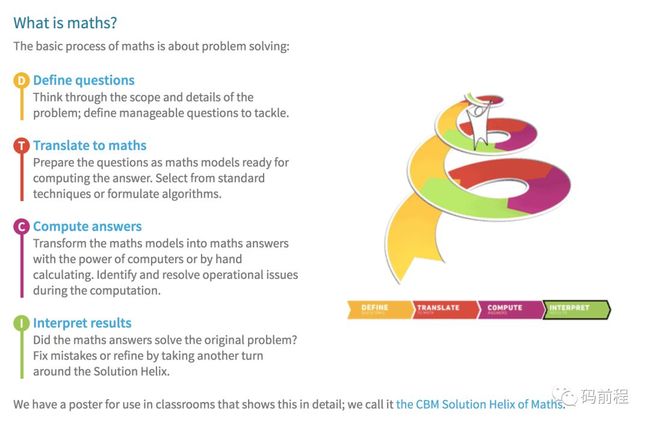
现在让我们考虑另一个问题。 数学是什么？ 当我们说我们在做数学， 或者说在教数学的时候我们指的是什么呢？ 总体来说，我觉得有四个步骤， 正确地提问是第一步。 我们想问的到底是什么问题？我们想了解的是什么？ 这步是在外部世界相比做数学的其他任何步骤中 最容易搞砸的一步。 如果人们问错了问题， 毫无疑问，他们会因此而得出错误的结果， 如果运算没有错误的话。 接下来就是根据正确的问题。 将它从现实世界的问题 转化成一个数学问题。 这就是第二步。 这样做之后我们就进入了运算的第三步骤。 求出某个 数学形式的答案。 当然，数学在这一方面非常有用。 最后，将解答转换成现实世界的问题。 这个答案有没有解决现实社会的问题呢？ 当然事实证明这也是关键一步。 现在，疯狂的事情就是 在数学教育中， 我们或许花了八成的时间 教人们用笔头计算解决第三个步骤。 然而，这恰恰是计算机 比任何经过多年运算训练的人都做得更好地一步。 换言之，我们本应该用计算机 去完成上述步骤三， 而让学生花更多的精力 去学好上述步骤一、二和四； 将问题概念化，并且运用它们， 让老师示范怎么去做。

看到了吗？这里的重点就是： 数学并不等同于计算。 数学是比计算更广泛的一门学科。 现在我们不难理解出现这种将计算和数学混淆在一起的原因了。 几百年来， 我们进行计算的唯一方法就是笔算。 仅仅是近几十年 这种情况才出现根本性的变化。 计算机的运用使任何古老学科 产生最大的变革成为了可能。 计算通常是有限步骤的， 无限步骤的并不常见。 因此，我觉得，虽然就事实而言，数学 已经从计算中解放出来。 但是数学的解放却仍没有被引入到教学之中。 我认为，在某种程度上，计算 只是机械化的数学。 计算是一种杂活， 就是那种你想尽量避免，可以的话让机器来完成的工作。 仅仅作为得出目的的手段，而不是目的本身。 而自动化允许我们 享用这种计算机器。 计算机允许我们这样做。 而这无论从何种角度看都不是一个小问题。 我估计，仅仅是今天世界范围之内， 我们就平均用了大约106年生命时间 去教人们做人工运算。 这是巨大的人类劳动。 因此我们最好可以非常确定—— 顺便提一下，绝大多数人做人工运算时没有感到任何乐趣。 因此，我们最好可以非常确定 我们知道这样做的原因， 这样做有一个真正的目的。

我认为我们应该预计计算机 可以完成运算， 仅仅在必要时才教人们人工笔头运算。 当然我觉得某些情况下 比如说，心算。 我现在仍然经常运用心算，通常是用来预估。 当别人说，答案是这样的， 我会说，嗯，不确定。 我认为答案大概是这样吧。 心算在这方面仍然是比较快速而且有用的。 因此我认为实用性是 其中一种值得教授人工运算的情况。 另外还有一些 同样得益于人工运算的概念， 但我认为这种情况相对来说比较少。 比如说，我经常会问起 以古希腊教学数学来做一个类比。 我们现在的教学 总是强迫学生去学习数学。 它是一个主科。 注意的是，我从来没有刻意暗示说如果有人对人工运算感兴趣 或者按照他们自己的意愿 学习任何哪怕是毫无意义的学科； 相反，他们应当这样做。 因为让人们发展自己的兴趣爱好， 完全就是一件正确的事。 我个人对古希腊怀有某种特殊的情结， 但我不认为我们应该逼迫全体人民 都像古希腊学习数学的方法。 我不认为这样是值得的。 因此我知道我们应该区分迫使人们学习 或是作为某种主流的学科 与人们在某种程度上自觉按照自己意愿学习的 或甚至是钟情于此的学科。

那人们为什么提出这一点呢？ 其中一点，他们会说，你必须先打好基础。 你在完全掌握学科的基础之前 不许用机器。 那我通常的疑问就是，你所说的“基础”指的什么？ 什么的基础？ 这样说来，请问驾车的基础 是否是怎样修车或者设计车模？ 而写作的基础是否又是要学习如何削鹅毛笔？ 我认为不是这样的。 我认为你需要将你所要做的事情的基础 理解成两部分如何得出结果 与用机器如何得出结果区分开来。 自动化允许你作出如此的理解。 一百多年前，如果要学车你无疑是需要 知道某些汽车机械原理的 以及定时打火器等各零部件的工作原理。 但是汽车的自动化 实现两类学问的划分， 也就是说驾车现在与汽车工程学 是相对独立的两个学科， 修车又是另外一回事。 正是自动化实现了这种区分， 不仅在驾车的例子中是这样的自动化， 因为我相信自动计算化也会在未来的数学中起同样的作用， 我们可以自主地选择怎样去做。 数学可以向更多实际运用的人 去传播。

关于基本技能又有另外一个观点。 我认为，人们混淆 发明工具的次序 与在教学中应当运用这些工具的次序。 不能因为纸比计算机先被发明，而人们就应该先在教学中运用纸张， 用纸张教数学不一定代表 你会比用计算机 更了解数学的基础。 我女儿的一则轶事为这一点做了生动地说明。 她很喜欢制作她所说的“纸制笔记本电脑”。 （笑声） 有一天，我问她：“我在你这个年纪的时候， 我都不会做这些。 你觉得是为什么呢？” 她很仔细地想了一两秒， 然后她说，“没有纸吗？” （笑声） 如果你在计算机和纸张的发明之后出生， 你学习数学究竟是先用纸张学习还是先用计算机学习其实并不重要， 你仅仅需要用最佳的工具来学习数学。

那另一个观点就是“计算机使数学变蠢。” 在一定程度上的确如此，如果你用计算机， 这仅仅是无需思考的按键操作， 但如果你进行人工笔头运算， 这完全又是智力训练。 我要说，这一点很困扰我。 我们难道真的以为 现在通常人们在学校里 学习的数学 真的比按照解题步骤做题学得多吗? 他们大都还在用不理解的原理去解答他们不明白的问题。 至少我认为如此。 更严重的是，他们在学校所学的知识根本已经不再实用。 或许50年前还在用，但现在已经不再使用了。 除了教育之外，他们都用计算机来完成。 要清醒地知道，计算机已经完全解决了这一问题， 事实上使它更容易理解。 而如今，像任何伟大的工具一样， 它们可以彻底无须动脑筋地操作， 就像将任何东西都变成一场多媒体的盛宴一样， 就像这个解方程的例子， 计算机就好比是老师-- 它给学生演示如何现在用笔头进行运算和解题。 这其实很荒谬。 为什么我们要用计算机来演示如何用笔算解题呢？ 明明计算机可以自行计算来解题。 完全是倒退了。

下面让我为你演示 计算机如何运算出更复杂的题目。 通常在学校里， 你会学习像解二次方程式这类题目。 但如果你用计算机来做， 你仅需要做代换。 就可以将它变成四次方程，运算上更复杂。 同样的原理仍然适用， 只是运算上更复杂。 而现实世界里的问题 的确就像这样复杂和难懂的， 甚至更加棘手的问题。 它们都不是我们学校数学中学的那些简单愚蠢的东西。 让我们想想外面的世界。 难道我们真的以为工程学和生物学 等其他 得益于计算机和数学的学问 会由于应用计算机而在某种程度上被明显削弱吗？ 我认为，恰恰相反。 我们在数学教育中的真正问题 并不是计算机使数学变得愚蠢， 而是我们现在的教学使问题变得愚蠢。 好，那人们提到的另一点 就是笔头运算的步骤在一定程度上 可以教导学生理解数学。 因此如果你做过很多例题， 你就可以算出答案， 你也可以更好地理解数学系统的基础。 我认为，这个观点里有一点是我非常认同的， 那就是我认为步骤和运算过程很重要。 但是在现代社会我们有一个绝佳的途径去这样做， 那就是编程。

现在多数程序和编码过程 大都以编程的方式写下来， 而这也是一种很好的方式 去鼓励学生更多的参与， 检验他们是否真正理解数学问题。 如果你真的想检验你是否理解数学 就尝试编写一条程序。 因此我认为编程就是我们应该做的方向。 一言以蔽之，在此我想说的是 编程为我们提供了一个独特的机会： 一方面使数学更实用， 同时另一方面又更加理论化。 我想，这种在数学教学的新局面在其他任何学科都还没有出现。 这通常像是一种 在职业规划或者是智力培养之间的两难选择。 但我想运用计算机我们可以两方面同时实现。 还为我们又打开了许多可能性。 我们可以解决更多的实际问题。 我真切地感觉到这种教育的改革 可以让学生获得很多的知识和经验 比之前多得多的直观的认识和经验的累积。 和接触更加复杂的题目—— 畅游于数学的乐园，与数学沟通， 感受数学之美。 我们希望学生可以本能地感受数学。 而这恰恰是计算机使这成为可能。

另一点是计算机使我们得以对教学课程重新排序。 以前是按照计算的难度编排课程教学的顺序， 但现在我们可以重新排序， 按照概念理念的难度， 而不管计算的难度。 因此微积分传统上是很晚才能教授的项目。 原因是什么呢？ 问题就在于微积分的计算相当困难。 但事实上许多概念 是可以向更低年级的学生传授的。 这就是一个我为女儿所建的模型例子。 而且非常简单易懂。 这个模型是用于理解 当多边形的边数增加时，图形的变化随之改变。 当边数增加到非常大的时候， 当然，多边形变成一个圆。 顺便一提，她对可以转换颜色这一点 特别乐此不疲， 这也是这个展示的一个重要的特征。 你可以看到这是一个 对极限和微积分非常初步的启蒙， 也可以让你直观地看到趋于极限时所发生的变化， 无限小边数的情况和无限多边数的情况。 非常浅显的例子。 这是对世界的一种观察方式， 我们通常是很久很久之后才会教给学生这些。 但它却是对世界的一种非常重要且实用的观察。 那现在我们要改革 推进这个进程的路障 就在于考试。 最后，假如我们考试的方式是人工笔算， 就难以将目前的课程设计 改革成 在教学中可以使用计算机。

而既然作为一个如此重要的原因 在考试中使用计算机也是非常重要的。 如此以来，我们就可以设置实际的问题， 比如说，“哪一种人寿保险的险种更适合我们？” 人们实际生活中遇到诸如此类的问题。 你可以看到，这就不是那些愚蠢的问题模型。 这是一个我们优化选择时可以用到的实际模型。 我需要多少年的险期？ 这对保险费有什么影响？ 对利率等其他的影响呢？ 这里我没有刻意在暗示 这是考试中应该考的唯一类型的问题， 但是我认为至少这是非常重要的一类型， 也是目前的教育完全忽视的， 这对人们的实际理解也是至关重要的。

因此我相信 我们需要一场以计算机作为数学教学工具的改革。 我们务必确保 通过让人们可以切实感受数学， 我们才可以推进经济发展和 社会进步。 这绝不是可有可无的一环。 而我认为首先这样做的国家 一定会鹤立鸡群， 甚至取得更大的经济成就， 更完善的经济体系， 和更卓越的国家面貌。 事实上，我甚至会说我们正在 从我们现在经常提到的“知识经济”时代迈向 可能被称作“计算机知识经济”的时代， 高端的数学知识对每个人 应用现代知识来说都不可或缺。 我们可以让更多学生加入到这个改革， 让他们在最佳的时机得到这样的教育。 我们要明白 这不是一场渐进式的改革。 我们要试图跨越 学校数学和实际数学之间的鸿沟。 你可以看到如果我们是走过这个鸿沟的话， 我们一定会跌得粉身碎骨， 甚至比没有开始改革更糟糕。 这不是我想要的局面， 我想说，我们应该跳跃， 我们必须加快我们的起跳速度， 这样我们就可以跳得高， 我们应该从鸿沟的一头跳到另外一头， 当然要准确地计算这里微分方程。

因此我想看到的是 一套全新的、经过改良的数学教学课程 在应用计算机的基础上 架构而起， 目前计算机已经是在各地非常普遍的 运算工具， 相信在不久的将来它会彻底覆盖每一个地方。 现在我还不确定我们是否应该仍然沿用“数学”作为这个学科的名字， 但我确信 这门课将是未来学科的主流。 让我们共同努力吧。 并且在学习它的过程中 让大家 所有人，广大的学生以及TED这里的观众享受一些乐趣！

这个演讲的作者是康拉德·沃尔夫拉姆，主要致力于数学教育改革。康拉德·沃尔夫拉姆是通过使用信息技术推动数学教育改革的主要倡导者。并且是

computerbasedmath.org

的创建者。他认为：“有些情况用手动计算很重要，但是这只是很少数的情况。大部分时候你应该假设学生们应该使用电脑，就像现实生活中每个人都使用电脑来完成任务。” 而且“学校中的数学与实际生活中用来解决问题的数学严重脱节”。 在与 Guardian 的一次访谈节目中，他还把用计算机代替手动计算描述为 "民主化的能力"。

更深度的内容可以访问

http://www.conradwolfram.com/

进一步了解。

所以，牛顿的创造力不是天生的，而是后天的长期磨炼和思考学会的！

“终身幼儿园”是雷斯尼克教授在麻省理工学院的成立项目团队，这个创新团队始终致力于对青少年儿童后天创造力培养的研究。比如，他们发明了世界上首个专为儿童设计开发的计算机编程语言——Scratch，将复杂的编程过程像堆积木一样简单，从而带领无数的孩子敲开了编程世界的大门......