- 程序 = 数据结构 + 算法
- 程序好坏 = 时间复杂度 + 空间复杂度 + 应用场景
如何选择算法应用的场景:根据算法本身特点和应用场景 来选择。
算法的稳定与不稳定:
- 稳定:排序算法次数不会发生变化。稳定的算法经过改进后,基本变成不稳定。
- 不稳定:排序算法次数会发生变化
接下来总结8大内部排序算法和代码实现:
- 冒泡排序
- 选择排序
- 快速排序
- 归并排序
- 链式基数排序
- 插入排序
- 希尔排序
- 堆排序
1、冒泡排序
1. 应用场景:8个以内的数据,速度最快
2.算法思路:从前面2个进行大小比较,进行交换。然后依次比较。
3.也是属于蛮力法的一种,先来了解下蛮力法的概念:
蛮力法(brute force method, 也称为穷举法或枚举法)。是一种简单直接解决问题的方法,常常直接基于问题的描述,所以蛮力法也是最容易应用的方法。但是,用蛮力法设计的算法时间特性往往也是最低的,典型的指数时间算法一般都是通过蛮力法搜索而得到的。
代码
/**
* 蛮力法,冒泡排序
* 例子:3 1 5 8 2 9 4 6 7
* 时间复杂度:n*(n-1)/2 -> 趋近于n
* @param array
*/
public static void bubbleSort(int[] array){
for(int i=array.length-1;i>0;i--) {
boolean flag=true;
for (int j = 0; j < i; j++) {
if (array[j] > array[j + 1]) {
int temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
flag=false;
}
}
if(flag){//说明后面都是排好序的,不用排序了
break;
}
}
}
2、选择排序
1.应用场景:8个以内的数据,速度最快
2.算法思路:定位最前的一个值,然后在进行后面所有的值比较大小,找到最小的就和定位的那个值进行交换,然后依次进行。
代码
/**
* 选择排序法
* 例子:{1,2,5,8,3,9,4,6,7}
* @param array
*/
public static void selectSort(int[] array){
for(int i=0;i3、快速排序(前序)
应用场景:数据量大并且是线性结构,如果是链表,那么没有性能可言的。
短处:
- 有大量重复数据的时候,性能不好
- 单向链式结构处理性能不好(一般来说,链式都不使用)
代码
/**
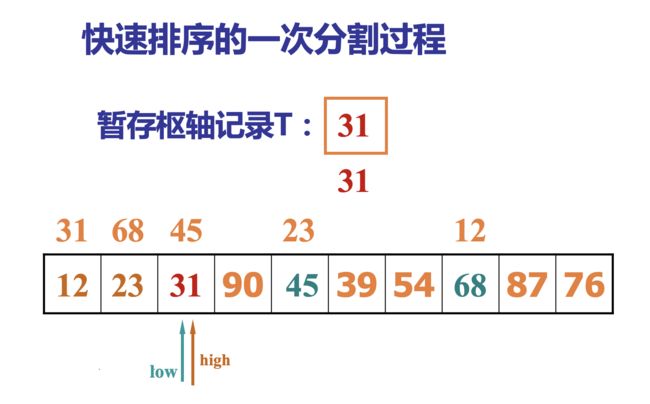
* 快速排序 31 21 59 68 12 40
* x=31
* @param array
* @param begin
* @param end
*/
//
public static void quickSort(int[] array,int begin,int end){
if(end-begin<=0) return;
int x=array[begin];
int low=begin;//0
int high=end;//5
//由于会从两头取数据,需要一个方向
boolean direction=true;
L1:
while(lowlow;i--){
if(array[i]<=x){
array[low++]=array[i];
high=i;
direction=!direction;
continue L1;
}
}
high=low;//如果上面的if从未进入,让两个指针重合
}else{
for(int i=low;i=x){
array[high--]=array[i];
low=i;
direction=!direction;
continue L1;
}
}
low=high;
}
}
//把最后找到的值 放入中间位置
array[low]=x;
//开始完成左右两边的操作
quickSort(array,begin,low-1);
quickSort(array,low+1,end);
}
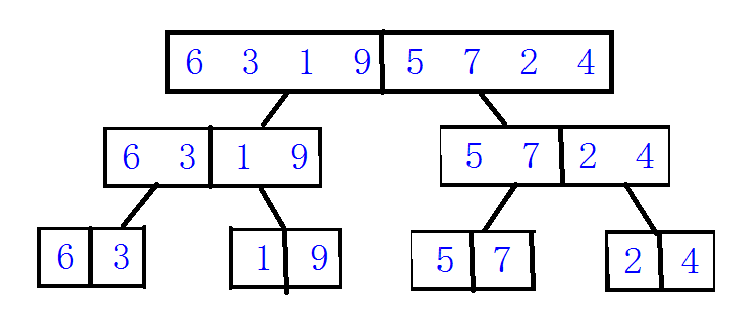
4、归并排序(后序)
应用场景:数据量大并且有很多重复数据,链式结构。
短处:需要空间大
代码
/**
* 归并排序
* @param array
* @param left
* @param right
*/
public static void mergeSort(int array[],int left,int right){
if(left==right){
return;
}else{
int mid=(left+right)/2;
mergeSort(array,left,mid);
mergeSort(array,mid+1,right);
merge(array,left,mid+1,right);
}
}
/**
* 归并排序
*
* 0 4 7
* 1 2 5 9 === 3 4 10 11
*
* @param array
* @param left
* @param mid
* @param right
*/
public static void merge(int[] array,int left,int mid,int right){
int leftSize=mid-left;
int rightSize=right-mid+1;
//生成数组
int[] leftArray=new int[leftSize];
int[] rightArray=new int[rightSize];
//填充数据
for(int i=left;i5、链式基数排序
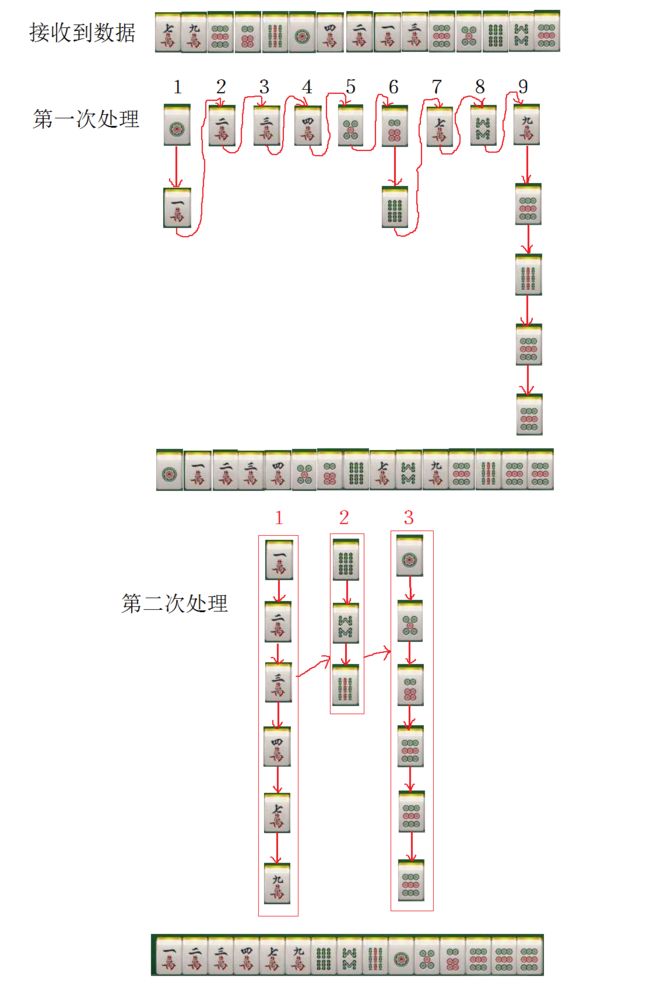
只适合几十个数据以内的情况。 数据量不大的情况下,用链式是非常快的。
例如:麻将的排序过程
代码
/**
* 基数排序
* author: bobo
* create time: 2018/12/11 2:08 PM
* email: [email protected]
*/
public class BaseSort {
/**
* 基数排序
*/
public static void radixSort(LinkedList list){
//对应点数进行分组
LinkedList[] rankList = new LinkedList[9];
for (int i = 0; i < rankList.length; i++) {
rankList[i] = new LinkedList();
}
//把数据一个个放到对应的组中
while (list.size() > 0) {
//取一个
Mahjong m = list.remove();
//放到组中,下标=点数减1
rankList[m.rank - 1].add(m);
}
for (int i = 0; i < rankList.length; i++) {
list.addAll(rankList[i]);
}
//花色进行分组
LinkedList[] suitList = new LinkedList[3];
for (int i = 0; i < suitList.length; i++) {
suitList[i] = new LinkedList();
}
//把数据一个个放到组中
while (list.size() > 0) {
//取一个
Mahjong m = list.remove();
//放到组中,下标=点数减1
suitList[m.suit - 1].add(m);
}
//把3个组合到一起
for (int i = 0; i < suitList.length; i++) {
list.addAll(suitList[i]);
}
}
class Mahjong {
public int suit;// 花色 筒 万 索
public int rank;// 点数,一 二 三
public Mahjong(int suit, int rank) {
this.suit = suit;
this.rank = rank;
}
@Override
public String toString() {
return "("+this.suit+" "+this.rank+")";
}
}
}
测试
@Test
public void testMahjong (){
LinkedList list=new LinkedList();
list.add(new Mahjong(3,1));
list.add(new Mahjong(2,3));
list.add(new Mahjong(3,7));
list.add(new Mahjong(1,1));
list.add(new Mahjong(3,8));
list.add(new Mahjong(2,2));
list.add(new Mahjong(3,2));
list.add(new Mahjong(1,3));
list.add(new Mahjong(3,9));
System.out.println("排序之前:" + list);
radixSort(list);
System.out.println("排序之后:" + list);
}
结果
排序之前:[(3 1), (2 3), (3 7), (1 1), (3 8), (2 2), (3 2), (1 3), (3 9)]
排序之后:[(1 1), (1 3), (2 2), (2 3), (3 1), (3 2), (3 7), (3 8), (3 9)]
6、插入排序
应用场景:主要是为希尔排序做准备的
例如:玩扑克牌的过程中,在一张一张摸牌的手机,会直接在手中插入牌,并排好序。
代码
/**
* 插入排序
*
* @param array
*/
public static void insertSort(int[] array) {
for (int i = 1; i < array.length; i++) {
int k = i;
int target = array[k];
while (k > 0 && target < array[k - 1]) {
array[k] = array[k - 1];
k--;
}
array[k] = target;
}
}
测试
@Test
public void main() {
int[] array = {8, 5, 7, 3, 6, 4, 1, 2, 9};
insertSort(array);
System.out.print("插入排序:");
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + " ");
}
}
结果:
插入排序:1 2 3 4 5 6 7 8 9
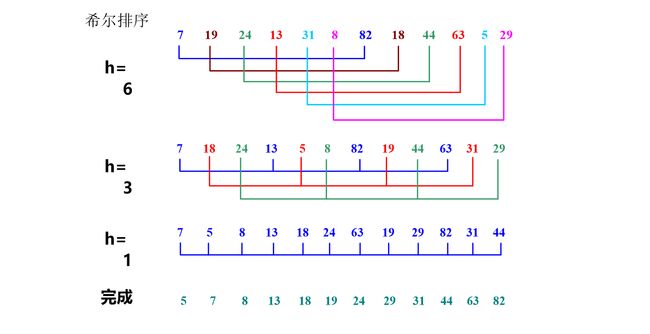
7、希尔排序
应用场景:在插入排序的基础上,适合数据量在中等的情况,几十个到几万个。
比如: 麻将在玩的过程中的重复排序(因为数据源本身即是有序)
概念:已知的最好步长序列由Marcin Ciura设计(1,4,10,23,57,132,301,701,1750,…)
这项研究也表明“比较在希尔排序中是最主要的操作,而不是交换。” 用这样步长序列的希尔排序比插入排序和堆排序都要快,甚至在小数组中比快速排序还快, 但是在涉及大量数据时希尔排序还是比快速排序慢。
-
代码
/** * 希尔排序 * * @param array 数组 * @param step 步长 */ public static void shellSort(int[] array, int step) { for (int j = 0; j < step; j++) { //直接插入排序 for (int i = j + step; i < array.length; i = i + step) { int k = i; int target = array[k]; while (k > step - 1 && target < array[k - step]) { array[k] = array[k - step]; k = k - step; } array[k] = target; } } } 测试: @Test public void main() { int[] array = {8, 5, 7, 3, 6, 4, 1, 2, 9}; shellSort(array, 3); shellSort(array, 1); System.out.print("希尔排序:"); for (int i = 0; i < array.length; i++) { System.out.print(array[i] + " "); } System.out.println(); } 结果: 希尔排序:1 2 3 4 5 6 7 8 9
8、堆排序
应用场景:在大数据情况下找到前n个数据
概念:堆排序(英语:Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
-
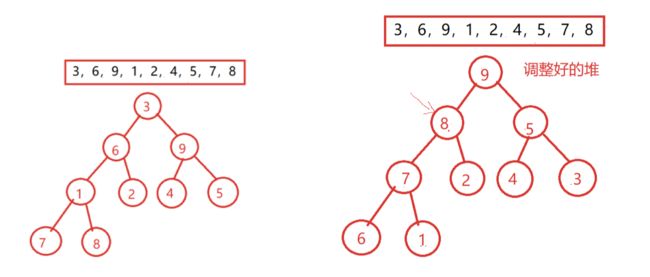
堆排序的过程:
- 从最后一个非叶子节点开始,每三个节点做一次大小比较,最小的做根
如果移动过程中如果子树上的顺序被破坏了,子树上重新调整三个节点的位置 - 取走整个树的根节点,把最后一个叶子做为根节点
- 重复1和2,直到所有节点被取走了
- 从最后一个非叶子节点开始,每三个节点做一次大小比较,最小的做根
-
完全二叉树链式结构和线性结构的换算
如果当前节点是 k
- 父节点是:(k-1)/2
- 左孩子是: 2 * k + 1
- 右孩子是: 2 * k + 2
时间复杂度为:O(nlogn)
- 代码:
/**
* 堆排序
* @param array
* @param len
*/
public void heapSort(int array[], int len) {
//建堆 len/2-1最后一个非叶子节点
for (int i = len / 2 - 1; i >= 0; i--) {
maxHeapify(array, i, len - 1);
}
//排序,根节点和最后一个节点交换
//换完以后,取走根,重新建堆
//len-1 最后一个节点
for (int i = len - 1; i > 0; i--) {
int temp = array[0];
array[0] = array[i];
array[i] = temp;
maxHeapify(array, 0, i - 1);
}
}
/**
* 调整堆
*/
public void maxHeapify(int array[], int start, int end) {
//父亲的位置
int dad = start;
//儿子的位置
int son = dad * 2 + 1;
while (son <= end) {//如果子节点下标在可以调整的范围内就一直调整下去
//如果没有右孩子就不用比,有的话,比较两个儿子,选择最大的出来
if (son + 1 <= end && array[son] < array[son + 1]) {
son++;
}
//和父节点比大小
if (array[dad] > array[son]) {
return;
} else {//父亲比儿子小,就要对整个子树进行调整
int temp = array[son];
array[son] = array[dad];
array[dad] = temp;
//递归下一层
dad = son;
son = dad * 2 + 1;
}
}
}
测试:
@Test
public void main() {
int[] array = {8, 5, 7, 3, 6, 4, 1, 2, 9};
heapSort(array, array.length);
System.out.print("堆排序: ");
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + " ");
}
}
结果:
堆排序: 1 2 3 4 5 6 7 8 9