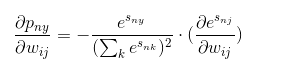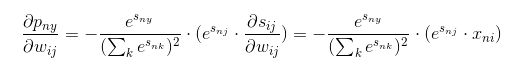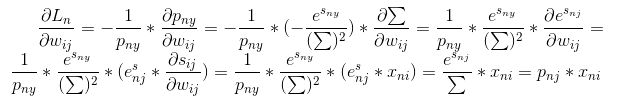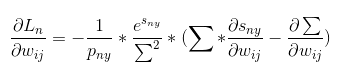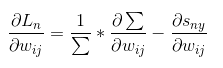首先说明,求导不只是链式法则这么简单。我们常常不知道需要对谁求导,如何利用从最后的损失函数一步一步的计算到参数上。此外,我们也有可能遇到不知道根据公式来进行编程,根本原因在于公式和编程并不是同样的语言,这是有差别的,我们如何跨越这个差别呢?
如果你有以上两个困惑,希望本文和下一篇博客能助你一臂之力。
本文主要针对第一个问题。第二个问题将会在下篇博客详细说明。
损失函数的计算
首先说明本文解决的是softmax的多分类器的梯度求导,以下先给出损失函数的计算方式:
这里将最终的loss分为4步进行计算,如下所示,当然,这里不解释为什么是这样的计算方式。
注意到,本文并不限制训练样本的数量,训练样本的特征数,以及最后分为几类。
这里x表示输入,w表示权重参数。
说明:这里的x和w的下标表示x的某一行和w的某一列相乘在逐项相加得到s。
然后再根据s计算每一个类的概率,如下公式(2)
这里采用的下标和公式(1)不相同,其中,n表示样本的个数,y表示样本为n时的正确分类标号。k表示有多少分类。这个公式就是先将s进行e次方计算,然后归一化,求得该样本正确分类下的概率p.
根据p可以计算出每一个样本的损失,如公式(3):
这个公式说明,每一个样本的损失仅仅是正确分类对应的概率值的log函数,这里准确说应该是ln函数,也就是以自然对数为底的,这样计算导数更方便,后面会以ln为版本进行计算。
最后,根据公式(4)计算所有样本的损失:
也就是将所有样本的损失求平均数。
注意:以上下标是独立系统,与下面的推导过程没有必然关系,这里特别指ij,其他字母的含义基本相同。
基本求导法则
所谓梯度,就是求损失函数对参数w的导数,将其用在更新参数w上,达到优化的目的。
我们知道,梯度计算遵循着链式法则,而基本求导公式也是需要的,防止有人忘记,我先给出这里将会用到的基本求导公式。知道的请跳过这一节,直接看下一节。
以下开始正式求梯度
计算整个损失函数对w(下标为ij)的导数。
根据链式法则,考虑到总损失为每个样本损失的平均数,且每个样本的损失都与wij相关,这个说明很有必要,假如某个损失与wij无关,我们就不用对它进行求导了。有公式(5)
这里Ln表示样本为n时的损失函数。
不失一般性,这里对最后一项进行继续推导,然后将其相加。
同样的,由于pny是和wij的函数,有公式(6):
结合公式(2),前一部分有有公式(7):
后一个部分我们继续来考虑,pny的上下两项是否都是wij的函数?肯定的回答是,这不一定,由公式(2)和(1)可知,如果公式2中分子的下标y不是j,那么实际上这里公式2的分子就不是wij的函数。
我们细说一下,由公式1,ij是公式1中的下标,当sij与wij有关系建立在这个j相等的情况,但是公式2的分子并不一定就满足这个关系的,什么情况满足呢?那就是样本n的正确分类的下标j和wij中的下标j相等时;否则这就没有关系。
因此,我们需要分为两种情况来进一步计算公式(6)的后半部分。
(实际上,我们也可以先认为他们相关,然后进一步处理,这里我先不这么做)
情况一,公式(2)中的分子与wij无关:也就是以下公式中y与j不相等
公式(2)中分母必然与wij有关,且只有一个与wij有关。那就是公式(2)中分母的下标k与wij的就相等时,而其他都与wij无关。
进一步考虑到e的s次方,s与wij的关系,因此针对情况一,有公式(8)
继续对第二项展开有公式(9):
这里还是细细说一下,这个过程,始终记住一点,那就是中间变量与wij是什么关系,可以根据公式看出来。根据公式(1),当且仅当s的下标中是ij时才会与wij有关,而对sij对wij求导时得到的就是xii,(两个i不一样的含义)只需要把公式(1)中的x和w的下标中的点号换成i即可。也就是说,s对w求导时,x的第一个下标是s的第一个下标,x的第二个下标是w的第一个下标。当然,这里我们需要再将s的下标i换成n,这样才能满足以上的推导。
我们将公式(9)根据公式(2)化简一下,再带入公式(6),可以得到公式(10),也就是情况一下的最终一个样本的梯度:
其中,用了一个简写,也就是求和的项简写了,请留意。
写成pnj是因为我们计算过程中会产生这个数,而且这样写起来也更整齐。
情况二,公式(2)中的分子是wij的函数:
注意到这里,公式(2)中pny的下标y和wij的下标j是相等的,也就是y=j。
情况2比情况1复杂在公式(2)的分母上,其余相同,因此,对其求导过程如下:
这里先使用ynj(nj是下标)表示样本为n时第j个分类的真实值,要么是0,要么是1,1表示真实分类就是这个j.
情况一根据(1\u)'求导,情况二则根据(v/u)'来求导,因此有一点差别。
以下一步一步的写:
根据公式(2)将后面展开可得:
化简一下可以得到:
根据公式(2)继续化简:
对上式去括号操作:
继续求导并且根据公式2化简得公式(11)
可以看出,这与上面的情况一相差在最后一项上,而前面一项是相等的。
接下来我们一起探讨一下怎么求后面的一项,毕竟这还无法完全理解清楚,因为这还是一个导数,也不是输入或者中间求到的某个数。
前面我们已经说到,情况二下公式(2)中的y和wij的j是相等的。
这时候计算知道:
所以公式(11)进一步计算可得最终的求导公式:公式(12)
综合两个情况
情况二比情况一多减去一项。
一般情况下,我们直接使用pnj * xni即可。
而当wij中j是当前样本n的正确分类时要多减去xni。
为了合并上面两种情况,我们构建一个矩阵,认为第一种情况是特殊情况,而第二种情况是一般情况。
那么,如果假设导数为 x的转置乘以上面求的概率p矩阵减去一个矩阵,这个矩阵需要满足在正确分类上为1,其他分类上为0.
因此,这个矩阵大部分是0,而如果用每一行表示一个样本的话,那么每一行就有一个正确分类,也就是说每一行正确分类上就是1,其他为0.
我们可以将这个矩阵认为是一个掩膜。
举例说明:假如我们有两个样本,也只有两个类别,样本分别为(1,2,3) (4,5,6)。这两个样本的特征是3个(这里故意使样本数和特征数不相等),而这两个样本的正确分类是分别是猫,和车(猫是class1, 车是class2)。
因此,上述矩阵就是【1,0】【0,1】
最后,总的公式就是:
其中,x就是输入,T表示转置。p就是softmax的输出概率;matrix就是上述说的矩阵,其中正确分类的标签上是1,其他都是0。
以上就是是多分类器softmax的梯度求导公式。
总结
求导过程有一些需要注意的地方:
1)链式法则是基本原理,但需要我们自己弄清楚谁是谁的函数,对谁求导;
2)遇到不同的情况可以分开对待,也可以先统一看待;
3)可以分多步进行,刚开始不要一步登天;
4)适当保留中间计算数据,最终求导可能会用到;
5)要弄清楚下标的操作,注意损失函数的计算下标和求导的下标通常不一样。
后话
其实个人感觉梯度的计算还是挺难的,而且本文只是推导公式,还没有真正的编程计算。
实际上,我们通常为了保证我们的程序正确,会写一个数值求导,正确情况下两者不会相差很多。
本文的理论推导,将会在下一篇博客中写明如何进行计算。