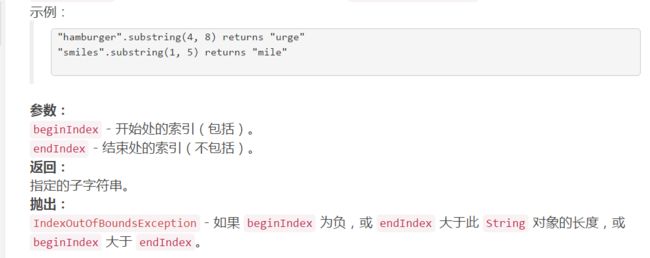
本文是算法之美一书的第一部分(自己分的),着重讲解一下字符串的匹配问题。
字符串的精确匹配有BF、MP、KMP、BM、BMH算法等;模糊匹配有全局编辑向量、局部最佳对准、N元距离模型、语音编码模型等。
字符串精确匹配:
BF算法:
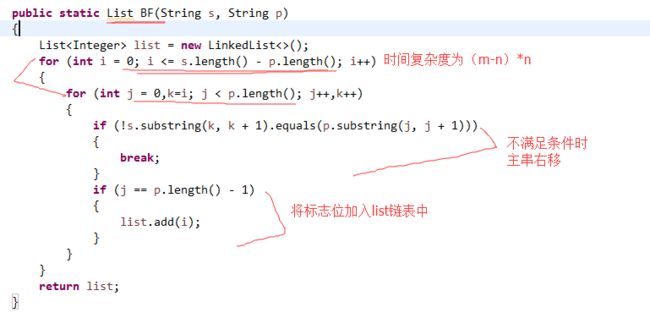
算法思路:最简单的字符串模式匹配方式:时间复杂度最高,为平方级别。
MP算法(快速串匹配算法):
首先通过模式串建立mpNext()数组,该数组的功能时在计算失效函数(假设j=3,比较p0p1p2?=p1p2p3,若相等,f(j)=3-1;不等,则比较p0p1?=p1p2;f(j)=2-1;类推,若都不等,则为-1)的基础上加1,同时多设置一位表示串匹配成功而主串未完时继续比较的情况,即mpNext[length]=0。
注:加1这个地方是不对的:而是通过Pf(j-1)+1得到mpNext[j]的值。
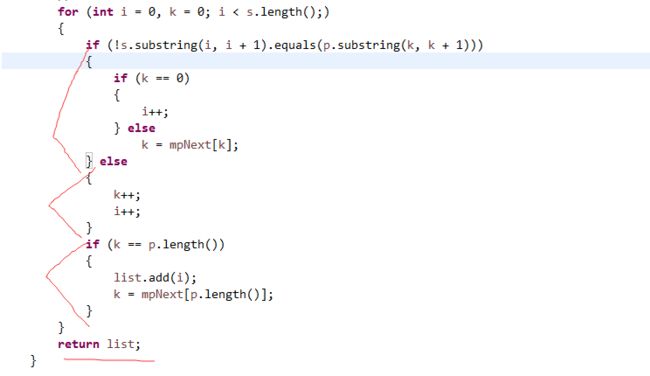
建立之后,开始遍历主串:若第一个就不等,主串++;模式串=0;若相等,则++、++;若并非第一个不等,则主串不变,模式串=mpNext[k]。
将i存入list链表中。(以消耗空间代替消耗时间)
代码如下:
KMP算法:
KMP与MP的不同之处在于:MP针对一些模式字符串未能完全跳到最优的字符下所做的一点改进。
算法建立在mpNext基础之上,遵循以下四个原则:
(1)mp=0且pj(j位的字符)=p0,kmp=-1;
(2)mp=0且pj!=po,则kmp=0;
(3)mp!=0且pj!=pmp,kmp=mp;
(4)mp!=0且pj==pmp, 则将mp的值换为原来mp中的j值,知道前三种情况出现,求得kmp。
说明:对于文本的精确匹配,还有好多,比如BM算法:自左向右移动,自右向左比较、BMH算法等。
字符串模糊匹配:
全局编辑向量
基本思想为:对两个字符串建立一个(m+2)*(n+2)的二维表格,并将第二行第二列设置为0。从第三行第三列开始,计算每一位上的值,计算的方法为:查看左上角、左方、上方的值,选择最大值并加上两字符的比较结果(相同+1、不同-1),从而得到最终结果即为最后一个数。之后回溯,根据那条路径得到的最值,挑选出此路径即可(注意此路径不止一条)。
以GCATGCA 与GATTACA为例,得到最值2并得到回溯结果后,便可得到可能的匹配结果:
GCATG_CA GCA_TGCA GCAT_GCA
G_ATTACA G_ATTACA G_ATTACA
观察可以发现,最小匹配结果都是5次成功、一次失败、2次插入或者删除操作。最终得到的结果为5-1-2=2.
局部最佳对准
与全局编辑距离的不同之处仅在于当有负数出现时将负值变为0即可。
时间与空间复杂度同样是O(mn)
N元距离模型
以Gorbachev 与 Gorbechyov举例:
首先的思路是计算他们每个的N元分组,即将字符串按n元分组,Go or rb ba ac ch he ev(假设n=2时),计算两字符串有多少个相同的子串。但这种方式在比较gril与grilfriend时,即使子串很多,也是不成立的。
所以,在此基础上加入距离模型: Gn1+Gn2-n*(Gn1交Gn2)
套入上例即为(8+9)-2*4=9。显然距离越小, 两个字符串越接近。
语音编码模型
运用发音规则对这些词进行模糊匹配将会得到非常理想的效果。基于语音编码和模糊匹配也是自然语言处理中的一个非常重要的话题。
soundex算法:将一个英文字符串转换为固定格式的编码格式,比如hrie 思路为保留H,同时查询字母编码转化表,将后面字母转化为数字(表中一个数组对应多个相近发音的字母)。最终得到比较结果。
soundex算法作为其他算法之父,普遍应用于MySQL、Oracle等主流数据库中。