前言

本教程来自TensorFlow官方教程 tensorflow.org,网站和大部分学习资源被墙，请自主进行科学上网。文章旨在记录自己学习机器学习相关知识的过程，如对您学习过程有所助益，不胜荣幸。文章是个人翻译，水平有限，希望理解。教程采用Anaconda版本的Python，是Python3代码,编辑器是Pycharm。

原文Github地址

原文colab地址(科学上网)

相比于判断图片是橘子还是苹果的分类问题，在一个回归问题中，我们的目标是预测一个连续的输出值，就像价格或者概率。
本次的教程将会建立一个模型来预测19世纪70年代中期波士顿郊区的房价。我们会提供给模型一些其他信息，例如犯罪率和当地的房地产税率。
在这个例子中我们会像之前那样使用keras库。你可以使用下面的代码来导入它：

import tensorflow as tf
from tensorflow import keras

import numpy as np

print(tf.__version__)

1.10.0

波士顿房价数据集

这个数据集现在也可以通过TensorFlow的代码可以直接获取。你可以使用下面代码来获取：

boston_housing = keras.datasets.boston_housing

(train_data, train_labels), (test_data, test_labels) = boston_housing.load_data()

# Shuffle the training set
order = np.argsort(np.random.random(train_labels.shape))
train_data = train_data[order]
train_labels = train_labels[order]

Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/boston_housing.npz
57344/57026 [==============================] - 0s 0us/step

样例和特点

这次的数据集相比之前小了不少：它仅有506个，并且404个用来训练，拿出102个用来当作测试数据集。

print("Training set: {}".format(train_data.shape))  # 404 examples, 13 features
print("Testing set:  {}".format(test_data.shape))   # 102 examples, 13 features

Training set: (404, 13)
Testing set:  (102, 13)

这个数据集包含了13个不同的特征属性：

人均犯罪率
占地面积超过25,000平方英尺的住宅用地比例。
每个城镇非零售业务的比例。
查尔斯河虚拟变量如果是大片土地则为1，否则为0
氮的氧化物浓度(分之1000万
平均每人所住房间数
1940年前业主单位所占的比例
到达波士顿就业中心的加权距离
到达径向公路的系数
所有财产价值的每10000美元的税率
城镇师生比例
城镇黑人比例按照式计算
地位较低人士的百分比

每一个输入数据的特征都以不同的大小存储着。有些特征值是0和1之间的浮点数，代表着百分比。有些可能是1到12之间的整数，有些则是0到100之间的整数。这些都是现实世界中数据的真实存在形式，理解并学会对这些数据的清理是一项重要的开发技能。

print(train_data[0])  # Display sample features, notice the different scales

[7.8750e-02 4.5000e+01 3.4400e+00 0.0000e+00 4.3700e-01 6.7820e+00
 4.1100e+01 3.7886e+00 5.0000e+00 3.9800e+02 1.5200e+01 3.9387e+02
 6.6800e+00]

我们可以使用pandas库的图表来更好的展示训练集中的几组数据：

import pandas as pd

column_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD',
                'TAX', 'PTRATIO', 'B', 'LSTAT']

df = pd.DataFrame(train_data, columns=column_names)
print(df.head())

    CRIM    ZN  INDUS  CHAS    NOX  ...     RAD    TAX  PTRATIO       B  LSTAT
0  0.07875  45.0   3.44   0.0  0.437  ...     5.0  398.0     15.2  393.87   6.68
1  4.55587   0.0  18.10   0.0  0.718  ...    24.0  666.0     20.2  354.70   7.12
2  0.09604  40.0   6.41   0.0  0.447  ...     4.0  254.0     17.6  396.90   2.98
3  0.01870  85.0   4.15   0.0  0.429  ...     4.0  351.0     17.9  392.43   6.36
4  0.52693   0.0   6.20   0.0  0.504  ...     8.0  307.0     17.4  382.00   4.63

标准化数据

建议对使用不同比例和范围的特征值进行标准化。对于每个特征值，减去特征值的平均值并除以标准偏差：

# Test data is *not* used when calculating the mean and std.

mean = train_data.mean(axis=0)
std = train_data.std(axis=0)
train_data = (train_data - mean) / std
test_data = (test_data - mean) / std

print(train_data[0])  # First training sample, normalized

[-0.39725269  1.41205707 -1.12664623 -0.25683275 -1.027385    0.72635358
 -1.00016413  0.02383449 -0.51114231 -0.04753316 -1.49067405  0.41584124
 -0.83648691]

尽管数据没有经过标准化时依然可以进行训练，但是这样会使训练难度提升，并且会导致模型过于依赖输入神经元。

创建模型

def build_model():
  model = keras.Sequential([
    keras.layers.Dense(64, activation=tf.nn.relu, 
                       input_shape=(train_data.shape[1],)),
    keras.layers.Dense(64, activation=tf.nn.relu),
    keras.layers.Dense(1)
  ])

  optimizer = tf.train.RMSPropOptimizer(0.001)

  model.compile(loss='mse',
                optimizer=optimizer,
                metrics=['mae'])
  return model

model = build_model()
model.summary()

这次的模型采用的都是全连接层。输出层是一个连续的函数值。

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense (Dense)                (None, 64)                896       
_________________________________________________________________
dense_1 (Dense)              (None, 64)                4160      
_________________________________________________________________
dense_2 (Dense)              (None, 1)                 65        
=================================================================
Total params: 5,121
Trainable params: 5,121
Non-trainable params: 0
_________________________________________________________________

训练模型

这次我们训练了500个epoch，并且把训练记录放在了history对象中：

# Display training progress by printing a single dot for each completed epoch.
class PrintDot(keras.callbacks.Callback):
  def on_epoch_end(self,epoch,logs):
    if epoch % 100 == 0: print('')
    print('.', end='')

EPOCHS = 500

# Store training stats
history = model.fit(train_data, train_labels, epochs=EPOCHS,
                    validation_split=0.2, verbose=0,
                    callbacks=[PrintDot()])

....................................................................................................
....................................................................................................
....................................................................................................
....................................................................................................
....................................................................................................

训练过程的数据都保存在了history里面，我们可以通过画图来查看训练过程：

import matplotlib.pyplot as plt


def plot_history(history):
  plt.figure()
  plt.xlabel('Epoch')
  plt.ylabel('Mean Abs Error [1000$]')
  plt.plot(history.epoch, np.array(history.history['mean_absolute_error']), 
           label='Train Loss')
  plt.plot(history.epoch, np.array(history.history['val_mean_absolute_error']),
           label = 'Val loss')
  plt.legend()
  plt.ylim([0,5])

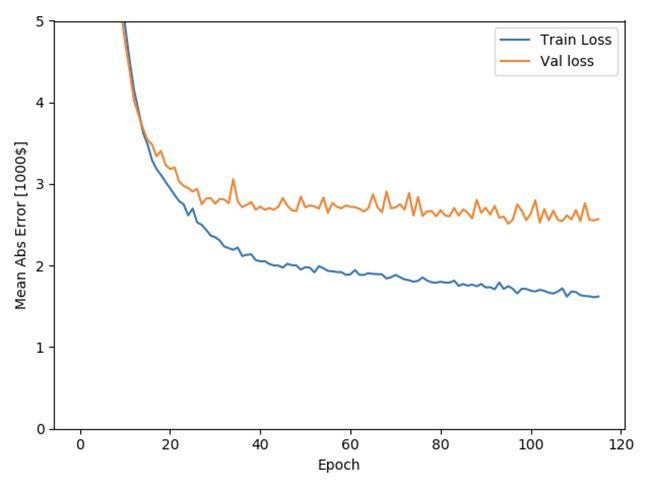
plot_history(history)

history

从图中可以看出，在200个epoch之后模型的提升率就很小了。我们可以通过更新一下模型的训练方式让模型在提升较小的时候停止训练。我们可以设置下面的回调函数来让模型自动停止训练：

model = build_model()

# The patience parameter is the amount of epochs to check for improvement.
early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', patience=20)

history = model.fit(train_data, train_labels, epochs=EPOCHS,
                    validation_split=0.2, verbose=0,
                    callbacks=[early_stop, PrintDot()])

plot_history(history)

....................................................................................................
................

history

训练好像确实提前终止了
图中显示平均误差值大概在

2500的误差对于那些只有$15000的标签值并不是一个微不足道的数目。
让我们看看我们的模型在测试数据上的表现如何：

[loss, mae] = model.evaluate(test_data, test_labels, verbose=0)

print("Testing set Mean Abs Error: ${:7.2f}".format(mae * 1000))

Testing set Mean Abs Error: $2679.54

预测

test_predictions = model.predict(test_data).flatten()

print(test_predictions)

[ 7.832362  18.450851  22.45164   34.88103   27.348196  22.26736
 26.963049  21.669811  19.895964  22.601202  19.965273  17.110151
 16.567072  44.0524    21.04799   21.103464  26.45786   18.709482
 20.825438  27.020702  11.160862  13.017411  22.807884  16.611425
 21.076998  26.213572  32.766167  32.652153  11.298579  20.164223
 19.82201   14.905633  34.83156   24.764723  19.957857   8.5664625
 16.906912  17.79298   18.071428  26.850712  32.625023  29.406805
 14.310859  44.013615  31.179125  28.41265   28.72704   19.22457
 23.301258  23.555346  37.15091   19.271719  10.640091  14.898285
 36.21053   29.63736   12.255004  50.43345   37.141464  26.562092
 25.075682  15.84047   15.081948  20.062723  25.168509  21.119642
 14.220254  22.637339  12.629622   7.517413  25.981508  30.909727
 26.12176   12.866787  25.869745  18.303373  19.470121  24.58047
 36.444992  10.777396  22.28932   37.976543  16.47492   14.191712
 18.707952  19.026419  21.038057  20.713434  21.794077  32.14987
 22.412184  20.55821   27.877415  44.4067    38.00193   21.748753
 35.57821   45.50506   26.612532  48.747063  34.60436   20.451048 ]

结论

这篇笔记介绍了一种解决回归问题的技巧：

均方误差（MSE）是一种适用于回归问题常见的损失函数。
在评估精度的时候回归问题是和分类问题不同的。在回归问题中我们使用了平均绝对误差（MAE）
当我们的输入数据的特征值在不同的范围内的时候，每一个特征值的大小都应该单独的进行缩放。
如果训练数据并不是太多，最好是选择比较小并且隐藏层比较少的神经网络模型来避免过度拟合
提前停止优化是一个比较有用的技巧来避免过度拟合。

#title MIT License
#
# Copyright (c) 2017 François Chollet
#
# Permission is hereby granted, free of charge, to any person obtaining a
# copy of this software and associated documentation files (the "Software"),
# to deal in the Software without restriction, including without limitation
# the rights to use, copy, modify, merge, publish, distribute, sublicense,
# and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL
# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
# DEALINGS IN THE SOFTWARE.

Tensorflow学习笔记之三：多元回归分析之房价预测

前言

波士顿房价数据集

样例和特点

标签

标准化数据

创建模型

训练模型

预测

结论

你可能感兴趣的:(Tensorflow学习笔记之三：多元回归分析之房价预测)